Question Number 94383 by niroj last updated on 18/May/20
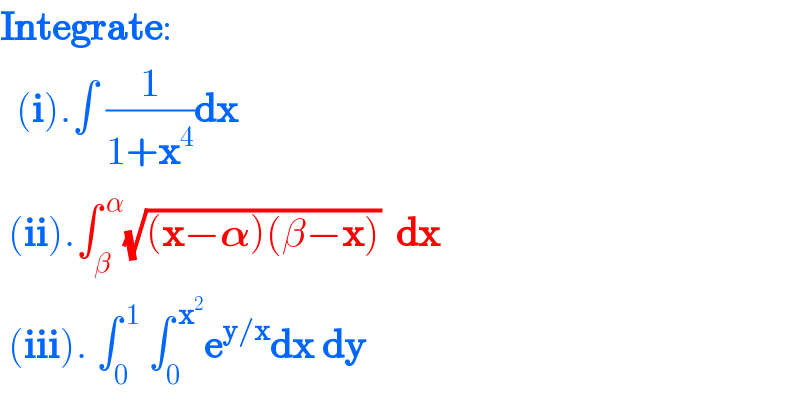
$$\boldsymbol{\mathrm{Integrate}}: \\ $$$$\:\:\left(\boldsymbol{\mathrm{i}}\right).\int\:\frac{\mathrm{1}}{\mathrm{1}+\boldsymbol{\mathrm{x}}^{\mathrm{4}} }\boldsymbol{\mathrm{dx}} \\ $$$$\:\left(\boldsymbol{\mathrm{ii}}\right).\int_{\beta} ^{\:\alpha} \sqrt{\left(\boldsymbol{\mathrm{x}}−\boldsymbol{\alpha}\right)\left(\beta−\boldsymbol{\mathrm{x}}\right)}\:\:\boldsymbol{\mathrm{dx}} \\ $$$$\:\left(\boldsymbol{\mathrm{iii}}\right).\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\int_{\mathrm{0}} ^{\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} } \boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{y}}/\boldsymbol{\mathrm{x}}} \boldsymbol{\mathrm{dx}}\:\boldsymbol{\mathrm{dy}} \\ $$
Answered by Mr.D.N. last updated on 18/May/20
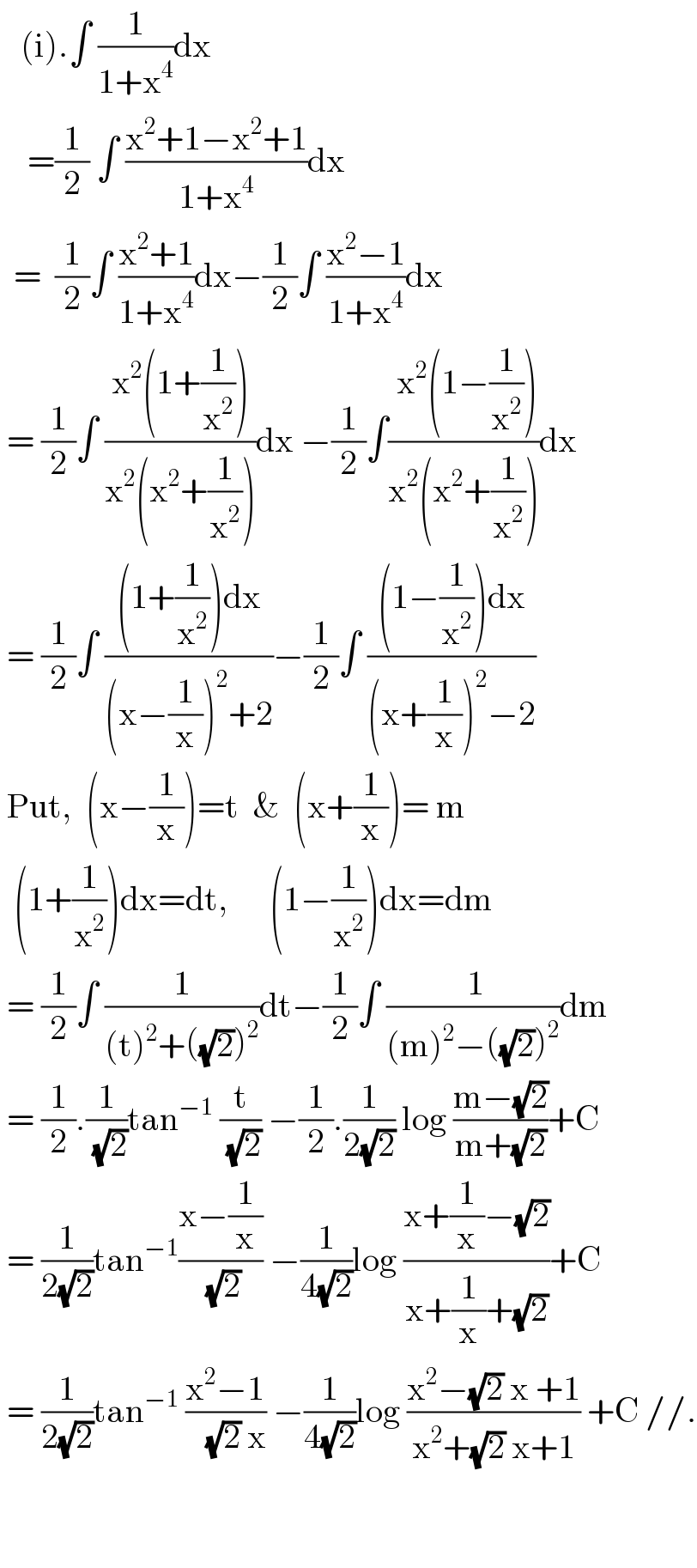
$$\:\:\:\left(\mathrm{i}\right).\int\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}\: \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx} \\ $$$$\:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)}\mathrm{dx}\:−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\:\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)}\mathrm{dx} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx}}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} +\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx}}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$$\:\mathrm{Put},\:\:\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{t}\:\:\&\:\:\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}\right)=\:\mathrm{m} \\ $$$$\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx}=\mathrm{dt},\:\:\:\:\:\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx}=\mathrm{dm} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{1}}{\left(\mathrm{t}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }\mathrm{dt}−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\:\mathrm{1}}{\left(\mathrm{m}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }\mathrm{dm} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{t}}{\:\sqrt{\mathrm{2}}}\:−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\mathrm{log}\:\frac{\mathrm{m}−\sqrt{\mathrm{2}}}{\mathrm{m}+\sqrt{\mathrm{2}}}+\mathrm{C} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}}{\:\sqrt{\mathrm{2}}}\:−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\mathrm{log}\:\frac{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}−\sqrt{\mathrm{2}}}{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{x}}+\sqrt{\mathrm{2}}}+\mathrm{C} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\:\:\:\sqrt{\mathrm{2}}\:\mathrm{x}}\:−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\mathrm{log}\:\frac{\mathrm{x}^{\mathrm{2}} −\sqrt{\mathrm{2}}\:\mathrm{x}\:+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\sqrt{\mathrm{2}}\:\mathrm{x}+\mathrm{1}}\:+\mathrm{C}\://. \\ $$$$\:\: \\ $$$$\:\:\: \\ $$
Commented by niroj last updated on 18/May/20
Excellent ����������
Commented by niroj last updated on 18/May/20
������
Commented by peter frank last updated on 18/May/20

$${thank}\:{you} \\ $$
Answered by Ar Brandon last updated on 18/May/20
![iii\ ∫_0 ^1 ∫_0 ^x^2 e^(y/x) dxdy=∫_0 ^1 x[e^(y/x) ]_0 ^x^2 dx=∫_0 ^1 x(e^x −1)dx=∫_0 ^1 x(e^x −1)dx [x∫(e^x −1)dx]_0 ^1 −∫_0 ^1 {(dx/dx)∫(e^x −1)dx}dx=[x(e^x −x)]_0 ^1 −∫_0 ^1 (e^x −x)dx =e−1−[e^x −(x^2 /2)]_0 ^1 =e−1−e+(1/2)+1=(1/2)](https://www.tinkutara.com/question/Q94387.png)
$$\mathrm{iii}\backslash\:\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{x}^{\mathrm{2}} } \mathrm{e}^{\mathrm{y}/\mathrm{x}} \mathrm{dxdy}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}\left[\mathrm{e}^{\mathrm{y}/\mathrm{x}} \right]_{\mathrm{0}} ^{\mathrm{x}^{\mathrm{2}} } \mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}\left(\mathrm{e}^{\mathrm{x}} −\mathrm{1}\right)\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}\left(\mathrm{e}^{\mathrm{x}} −\mathrm{1}\right)\mathrm{dx} \\ $$$$\left[\mathrm{x}\int\left(\mathrm{e}^{\mathrm{x}} −\mathrm{1}\right)\mathrm{dx}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\frac{\mathrm{dx}}{\mathrm{dx}}\int\left(\mathrm{e}^{\mathrm{x}} −\mathrm{1}\right)\mathrm{dx}\right\}\mathrm{dx}=\left[\mathrm{x}\left(\mathrm{e}^{\mathrm{x}} −\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{e}^{\mathrm{x}} −\mathrm{x}\right)\mathrm{dx} \\ $$$$=\mathrm{e}−\mathrm{1}−\left[\mathrm{e}^{\mathrm{x}} −\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{e}−\mathrm{1}−\mathrm{e}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by niroj last updated on 18/May/20
excellent dear..��������
Commented by Ar Brandon last updated on 18/May/20
��
Answered by mathmax by abdo last updated on 18/May/20
![I =∫_β ^α (√((x−α)(β−x)))dx ⇒I =∫_β ^α (√((α−x)(x−β)))dx we do the changement (√(α−x))=t ⇒α−x =t^2 ⇒x =α−t^2 ⇒ I = ∫_(√(α−β)) ^0 t(√(α−t^2 −β))(−2t)dt =2 ∫_0 ^(√(α−β)) t^2 (√(α−β−t^2 ))dt =_(t=(√(α−β))sinu) 2 ∫_0 ^(√(α−β)) (α−β)sin^2 u(√(α−β))cosu (√(α−β))cosu du =2(α−β)^2 ∫_0 ^(π/2) sin^2 u cos^2 u du =2(α−β)^2 ×(1/4)∫_0 ^(π/2) sin^2 (2u)du =(((α−β)^2 )/4)∫_0 ^(π/2) (1−cos(4u))du =(π/8)(α−β)^2 −(((α−β)^2 )/2)[(1/4)sin(4u)]_0 ^(π/2) =(π/8)(α−β)^2](https://www.tinkutara.com/question/Q94405.png)
$$\mathrm{I}\:=\int_{\beta} ^{\alpha} \sqrt{\left(\mathrm{x}−\alpha\right)\left(\beta−\mathrm{x}\right)}\mathrm{dx}\:\:\Rightarrow\mathrm{I}\:=\int_{\beta} ^{\alpha} \sqrt{\left(\alpha−\mathrm{x}\right)\left(\mathrm{x}−\beta\right)}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the} \\ $$$$\mathrm{changement}\:\sqrt{\alpha−\mathrm{x}}=\mathrm{t}\:\Rightarrow\alpha−\mathrm{x}\:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{x}\:=\alpha−\mathrm{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\:\int_{\sqrt{\alpha−\beta}} ^{\mathrm{0}} \:\mathrm{t}\sqrt{\alpha−\mathrm{t}^{\mathrm{2}} −\beta}\left(−\mathrm{2t}\right)\mathrm{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\sqrt{\alpha−\beta}} \:\:\mathrm{t}^{\mathrm{2}} \sqrt{\alpha−\beta−\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=_{\mathrm{t}=\sqrt{\alpha−\beta}\mathrm{sinu}} \:\:\:\mathrm{2}\:\int_{\mathrm{0}} ^{\sqrt{\alpha−\beta}} \:\:\left(\alpha−\beta\right)\mathrm{sin}^{\mathrm{2}} \mathrm{u}\sqrt{\alpha−\beta}\mathrm{cosu}\:\sqrt{\alpha−\beta}\mathrm{cosu}\:\mathrm{du} \\ $$$$=\mathrm{2}\left(\alpha−\beta\right)^{\mathrm{2}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{sin}^{\mathrm{2}} \mathrm{u}\:\mathrm{cos}^{\mathrm{2}} \mathrm{u}\:\mathrm{du}\:=\mathrm{2}\left(\alpha−\beta\right)^{\mathrm{2}} ×\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2u}\right)\mathrm{du} \\ $$$$=\frac{\left(\alpha−\beta\right)^{\mathrm{2}} }{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\mathrm{1}−\mathrm{cos}\left(\mathrm{4u}\right)\right)\mathrm{du} \\ $$$$=\frac{\pi}{\mathrm{8}}\left(\alpha−\beta\right)^{\mathrm{2}} \:−\frac{\left(\alpha−\beta\right)^{\mathrm{2}} }{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\left(\mathrm{4u}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\pi}{\mathrm{8}}\left(\alpha−\beta\right)^{\mathrm{2}} \\ $$
Commented by niroj last updated on 18/May/20
it's to be great����������
Answered by Mr.D.N. last updated on 18/May/20
![(ii). I= ∫_β ^( α) (√((x−α)(β−x))) dx =∫_β ^( α) (√(−x^2 +(α+β)x−αβ)) dx = =∫_β ^( α) (√((((β−α)/2))^2 −αβ−[x^2 −(α+β)x+(((β+α)/2))^2 ])) dx = ∫_β ^( α) (√((((β−α)/2))^2 −(x−((β+α)/2))^2 )) dx Put , ((β−α)/2) = a , and x − ((β+α)/2)= y Then dx=dy When x= α , y= α− ((β+α)/2)= ((α−β)/2)=−a When x=β , y= β − ((β+α)/2)= ((β−α)/2)= a ∴ I = ∫_(−a) ^( a) (√(a^2 −y^2 )) dy = [ ((y(√(a^2 −y^2 )))/2) + (a^2 /2) sin^(−1) (( y)/a)]_(−a) ^( a) = {0 +(a^2 /2)sin^(−1) (1) }−{ 0 +(a^2 /2)sin^(−1) (−1)} = (a^2 /2).(π/2)−(a^2 /2)(−(π/2))= (π/2)a^2 = (π/2)(((β−α)/2))^2 = (π/8)(β− α)^2 .](https://www.tinkutara.com/question/Q94401.png)
$$\:\:\left(\mathrm{ii}\right).\:\:\:\mathrm{I}=\:\int_{\beta} ^{\:\alpha} \sqrt{\left(\mathrm{x}−\alpha\right)\left(\beta−\mathrm{x}\right)}\:\:\mathrm{dx} \\ $$$$\:\:\:=\int_{\beta} ^{\:\alpha} \sqrt{−\mathrm{x}^{\mathrm{2}} +\left(\alpha+\beta\right)\mathrm{x}−\alpha\beta}\:\:\:\mathrm{dx} \\ $$$$\:\:=\:\:\:=\int_{\beta} ^{\:\alpha} \sqrt{\left(\frac{\beta−\alpha}{\mathrm{2}}\right)^{\mathrm{2}} −\alpha\beta−\left[\mathrm{x}^{\mathrm{2}} −\left(\alpha+\beta\right)\mathrm{x}+\left(\frac{\beta+\alpha}{\mathrm{2}}\right)^{\mathrm{2}} \right]}\:\mathrm{dx} \\ $$$$\:=\:\int_{\beta} ^{\:\alpha} \sqrt{\left(\frac{\beta−\alpha}{\mathrm{2}}\right)^{\mathrm{2}} −\left(\mathrm{x}−\frac{\beta+\alpha}{\mathrm{2}}\right)^{\mathrm{2}} }\:\:\mathrm{dx} \\ $$$$\:\:\mathrm{Put}\:,\:\frac{\beta−\alpha}{\mathrm{2}}\:=\:\mathrm{a}\:,\:\mathrm{and}\:\:\:\mathrm{x}\:−\:\frac{\beta+\alpha}{\mathrm{2}}=\:\mathrm{y} \\ $$$$\:\:\mathrm{Then}\:\:\mathrm{dx}=\mathrm{dy} \\ $$$$\:\:\mathrm{When}\:\:\:\mathrm{x}=\:\alpha\:,\:\:\mathrm{y}=\:\alpha−\:\frac{\beta+\alpha}{\mathrm{2}}=\:\frac{\alpha−\beta}{\mathrm{2}}=−\mathrm{a} \\ $$$$\:\:\mathrm{When}\:\mathrm{x}=\beta\:,\:\:\mathrm{y}=\:\beta\:−\:\frac{\beta+\alpha}{\mathrm{2}}=\:\frac{\beta−\alpha}{\mathrm{2}}=\:\mathrm{a} \\ $$$$\:\:\therefore\:\:\mathrm{I}\:=\:\int_{−\mathrm{a}} ^{\:\:\mathrm{a}} \sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }\:\mathrm{dy} \\ $$$$\:\:=\:\left[\:\frac{\mathrm{y}\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }}{\mathrm{2}}\:+\:\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}}\:\mathrm{sin}^{−\mathrm{1}} \frac{\:\mathrm{y}}{\mathrm{a}}\right]_{−\mathrm{a}} ^{\:\mathrm{a}} \\ $$$$\:\:=\:\left\{\mathrm{0}\:+\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \:\left(\mathrm{1}\right)\:\right\}−\left\{\:\mathrm{0}\:+\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(−\mathrm{1}\right)\right\} \\ $$$$\:=\:\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}}.\frac{\pi}{\mathrm{2}}−\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}}\left(−\frac{\pi}{\mathrm{2}}\right)=\:\frac{\pi}{\mathrm{2}}\mathrm{a}^{\mathrm{2}} \\ $$$$\:=\:\frac{\pi}{\mathrm{2}}\left(\frac{\beta−\alpha}{\mathrm{2}}\right)^{\mathrm{2}} =\:\frac{\pi}{\mathrm{8}}\left(\beta−\:\alpha\right)^{\mathrm{2}} . \\ $$$$ \\ $$
Commented by niroj last updated on 18/May/20
it's great done..������
