Menu Close

integrate-sin-2-xcos-2-x-sin-3-x-cos-3-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 52363 by Necxx last updated on 06/Jan/19
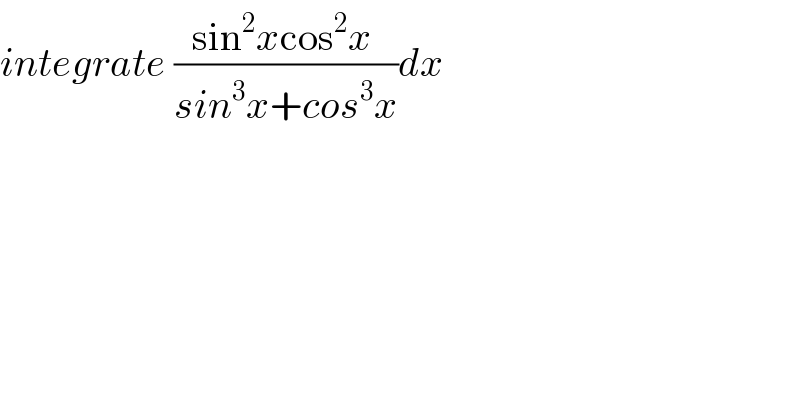
integrate ((sin^2 xcos^2 x )/(sin^3 x+cos^3 x))dx
$${integrate}\:\frac{\mathrm{sin}^{\mathrm{2}} {x}\mathrm{cos}^{\mathrm{2}} {x}\:}{{sin}^{\mathrm{3}} {x}+{cos}^{\mathrm{3}} {x}}{dx} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Jan/19
=(−1)∫((1−sin^2 xcos^2 x−1)/(sin^3 x+cos^3 x))dx =(−1)∫(((1+sinxcosx)(1−sinxcosx)−1)/((sinx+cosx)(1−sinxcosx)))dx =(−1)∫((1+sinxcosx)/(sinx+cosx))dx+∫(dx/(sin^3 x+cos^3 x)) =(((−1)/2))∫((1+(sinx+cosx)^2 )/((sinx+cosx)))+∫(dx/(sin^3 x+cos^3 x)) =(((−1)/2))∫(dx/(sinx+cosx))+(((−1)/2))∫(sinx+cosx)dx+ ∫(dx/(sin^3 x+cos^3 x)) I_1 =(((−1)/2))∫(dx/( (√2) ((1/( (√2) ))sinx+(1/( (√2)))cosx))) =(((−1)/(2(√2))))∫(dx/(sin(x+(π/4)))) =(((−1)/(2(√2))))∫cosec(x+(π/4))dx =(((−1)/(2(√2))))lntan(((x+(π/4))/2))=(((−1)/(2(√2))))lntan((x/2)+(π/8))←I_1 I_2 =(((−1)/2))∫sinx+cosx dx =(((−1)/2))[−cosx+sinx]←I_2 ∫(dx/(sin^3 x+cos^3 x)) t=tan(x/2) dt=(1/2)sec^2 ((x/2))dx ∫(((2dt)/(1+t^2 ))/((((2t)/(1+t^2 )))^3 +(((1−t^2 )/(1+t^2 )))^3 )) ?pls waitfor I_3
$$=\left(−\mathrm{1}\right)\int\frac{\mathrm{1}−{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}−\mathrm{1}}{{sin}^{\mathrm{3}} {x}+{cos}^{\mathrm{3}} {x}}{dx} \\ $$$$=\left(−\mathrm{1}\right)\int\frac{\left(\mathrm{1}+{sinxcosx}\right)\left(\mathrm{1}−{sinxcosx}\right)−\mathrm{1}}{\left({sinx}+{cosx}\right)\left(\mathrm{1}−{sinxcosx}\right)}{dx} \\ $$$$=\left(−\mathrm{1}\right)\int\frac{\mathrm{1}+{sinxcosx}}{{sinx}+{cosx}}{dx}+\int\frac{{dx}}{{sin}^{\mathrm{3}} {x}+{cos}^{\mathrm{3}} {x}} \\ $$$$=\left(\frac{−\mathrm{1}}{\mathrm{2}}\right)\int\frac{\mathrm{1}+\left({sinx}+{cosx}\right)^{\mathrm{2}} }{\left({sinx}+{cosx}\right)}+\int\frac{{dx}}{{sin}^{\mathrm{3}} {x}+{cos}^{\mathrm{3}} {x}} \\ $$$$=\left(\frac{−\mathrm{1}}{\mathrm{2}}\right)\int\frac{{dx}}{{sinx}+{cosx}}+\left(\frac{−\mathrm{1}}{\mathrm{2}}\right)\int\left({sinx}+{cosx}\right){dx}+ \\ $$$$\:\:\:\:\int\frac{{dx}}{{sin}^{\mathrm{3}} {x}+{cos}^{\mathrm{3}} {x}} \\ $$$${I}_{\mathrm{1}} =\left(\frac{−\mathrm{1}}{\mathrm{2}}\right)\int\frac{{dx}}{\:\sqrt{\mathrm{2}}\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}{sinx}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{cosx}\right)} \\ $$$$=\left(\frac{−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)\int\frac{{dx}}{{sin}\left({x}+\frac{\pi}{\mathrm{4}}\right)} \\ $$$$=\left(\frac{−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\right)\int{cosec}\left({x}+\frac{\pi}{\mathrm{4}}\right){dx} \\ $$$$=\left(\frac{−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\right){lntan}\left(\frac{{x}+\frac{\pi}{\mathrm{4}}}{\mathrm{2}}\right)=\left(\frac{−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\right){lntan}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{8}}\right)\leftarrow{I}_{\mathrm{1}} \\ $$$${I}_{\mathrm{2}} =\left(\frac{−\mathrm{1}}{\mathrm{2}}\right)\int{sinx}+{cosx}\:{dx} \\ $$$$=\left(\frac{−\mathrm{1}}{\mathrm{2}}\right)\left[−{cosx}+{sinx}\right]\leftarrow{I}_{\mathrm{2}} \\ $$$$\int\frac{{dx}}{{sin}^{\mathrm{3}} {x}+{cos}^{\mathrm{3}} {x}} \\ $$$${t}={tan}\frac{{x}}{\mathrm{2}}\:\:{dt}=\frac{\mathrm{1}}{\mathrm{2}}{sec}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right){dx} \\ $$$$\int\frac{\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }}{\left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{3}} +\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{3}} }\:\:?\boldsymbol{{pls}}\:\boldsymbol{{waitfor}}\:\boldsymbol{{I}}_{\mathrm{3}} \\ $$$$ \\ $$
Answered by MJS last updated on 07/Jan/19
∫((sin^2 x cos^2 x)/(sin^3 x +cos^3 x))dx=∫(((1−cos 4x)/8)/((3sin (x+(π/4))+cos (3x+(π/4)))/(2(√2))))dx= =((√2)/4)∫((1−cos 4x)/(3sin (x+(π/4))+cos (3x+(π/4))))dx= [t=x+(π/4) → dx=dt] =((√2)/4)∫((1+cos 4t)/(sin 3t +3sin t))dt=((√2)/4)∫((1−4sin^2 t cos^2 t)/((1+2cos^2 t)sin t))dt= =((√2)/4)∫((1+2sin^2 t)/((1+2cos^2 t)sin t))dt−((√2)/2)∫sin t dt= (1) ((√2)/4)∫((1+2sin^2 t)/((1+2cos^2 t)sin t))dt= [u=cos t → dt=−(du/(sin t))=−(du/( (√(1−u^2 ))))] =−((√2)/4)∫((2u^2 −3)/((u^2 −1)(2u^2 +1)))du= =((√2)/(24))∫(du/(u−1))−((√2)/(24))∫(du/(u+1))−((2(√2))/3)∫(du/(2u^2 +1))= =((√2)/(24))ln (u−1) −((√2)/(24))ln (u+1) −(2/3)arctan ((√2)u)= =((√2)/(24))ln ((cos t −1)/(cos t +1)) −(2/3)arctan ((√2)cos t) (2) −((√2)/2)∫sin t dt=((√2)/2)cos t =((√2)/(24))ln ((cos t −1)/(cos t +1)) −(2/3)arctan ((√2)cos t) +((√2)/2)cos t = =((√2)/(24))ln ((cos (x+(π/4)) −1)/(cos (x+(π/4)) +1)) −(2/3)arctan ((√2)cos (x+(π/4))) +((√2)/2)cos (x+(π/4)) = =((√2)/(24))ln ∣((2−(cos x −sin x)(√2))/(2+(cos x −sin x)(√2)))∣ −(2/3)arctan (cos x −sin x) +(1/2)(cos x −sin x) +C
$$\int\frac{\mathrm{sin}^{\mathrm{2}} \:{x}\:\mathrm{cos}^{\mathrm{2}} \:{x}}{\mathrm{sin}^{\mathrm{3}} \:{x}\:+\mathrm{cos}^{\mathrm{3}} \:{x}}{dx}=\int\frac{\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{8}}}{\frac{\mathrm{3sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)+\mathrm{cos}\:\left(\mathrm{3}{x}+\frac{\pi}{\mathrm{4}}\right)}{\mathrm{2}\sqrt{\mathrm{2}}}}{dx}= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{3sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)+\mathrm{cos}\:\left(\mathrm{3}{x}+\frac{\pi}{\mathrm{4}}\right)}{dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\frac{\pi}{\mathrm{4}}\:\rightarrow\:{dx}={dt}\right] \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{4}{t}}{\mathrm{sin}\:\mathrm{3}{t}\:+\mathrm{3sin}\:{t}}{dt}=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{\mathrm{1}−\mathrm{4sin}^{\mathrm{2}} \:{t}\:\mathrm{cos}^{\mathrm{2}} \:{t}}{\left(\mathrm{1}+\mathrm{2cos}^{\mathrm{2}} \:{t}\right)\mathrm{sin}\:{t}}{dt}= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{\mathrm{1}+\mathrm{2sin}^{\mathrm{2}} \:{t}}{\left(\mathrm{1}+\mathrm{2cos}^{\mathrm{2}} \:{t}\right)\mathrm{sin}\:{t}}{dt}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\mathrm{sin}\:{t}\:{dt}= \\ $$$$ \\ $$$$\:\:\:\:\:\left(\mathrm{1}\right)\:\:\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{\mathrm{1}+\mathrm{2sin}^{\mathrm{2}} \:{t}}{\left(\mathrm{1}+\mathrm{2cos}^{\mathrm{2}} \:{t}\right)\mathrm{sin}\:{t}}{dt}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{u}=\mathrm{cos}\:{t}\:\rightarrow\:{dt}=−\frac{{du}}{\mathrm{sin}\:{t}}=−\frac{{du}}{\:\sqrt{\mathrm{1}−{u}^{\mathrm{2}} }}\right] \\ $$$$\:\:\:\:\:=−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{\mathrm{2}{u}^{\mathrm{2}} −\mathrm{3}}{\left({u}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{2}{u}^{\mathrm{2}} +\mathrm{1}\right)}{du}= \\ $$$$\:\:\:\:\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{24}}\int\frac{{du}}{{u}−\mathrm{1}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{24}}\int\frac{{du}}{{u}+\mathrm{1}}−\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\int\frac{{du}}{\mathrm{2}{u}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$\:\:\:\:\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{24}}\mathrm{ln}\:\left({u}−\mathrm{1}\right)\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{24}}\mathrm{ln}\:\left({u}+\mathrm{1}\right)\:−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{u}\right)= \\ $$$$\:\:\:\:\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{24}}\mathrm{ln}\:\frac{\mathrm{cos}\:{t}\:−\mathrm{1}}{\mathrm{cos}\:{t}\:+\mathrm{1}}\:−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}\mathrm{cos}\:{t}\right) \\ $$$$ \\ $$$$\:\:\:\:\:\left(\mathrm{2}\right)\:\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\int\mathrm{sin}\:{t}\:{dt}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{cos}\:{t} \\ $$$$ \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{24}}\mathrm{ln}\:\frac{\mathrm{cos}\:{t}\:−\mathrm{1}}{\mathrm{cos}\:{t}\:+\mathrm{1}}\:−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}\mathrm{cos}\:{t}\right)\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{cos}\:{t}\:= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{24}}\mathrm{ln}\:\frac{\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)\:−\mathrm{1}}{\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)\:+\mathrm{1}}\:−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)\right)\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)\:= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{24}}\mathrm{ln}\:\mid\frac{\mathrm{2}−\left(\mathrm{cos}\:{x}\:−\mathrm{sin}\:{x}\right)\sqrt{\mathrm{2}}}{\mathrm{2}+\left(\mathrm{cos}\:{x}\:−\mathrm{sin}\:{x}\right)\sqrt{\mathrm{2}}}\mid\:−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arctan}\:\left(\mathrm{cos}\:{x}\:−\mathrm{sin}\:{x}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:{x}\:−\mathrm{sin}\:{x}\right)\:+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *