Question Number 36947 by maxmathsup by imad last updated on 07/Jun/18
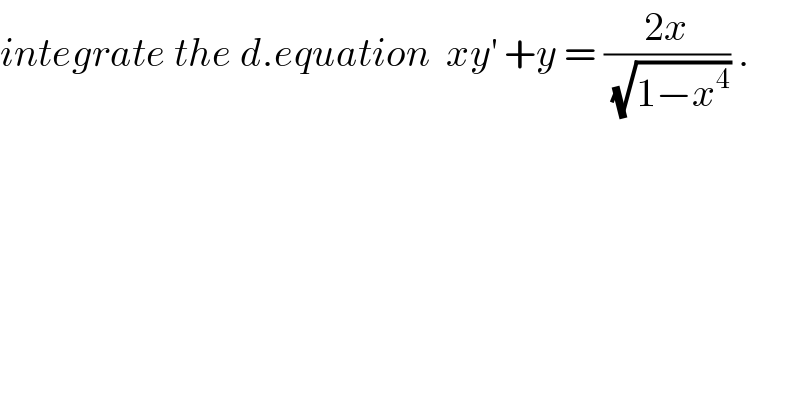
$${integrate}\:{the}\:{d}.{equation}\:\:{xy}^{'} \:+{y}\:=\:\frac{\mathrm{2}{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}\:. \\ $$
Commented by abdo.msup.com last updated on 07/Jun/18
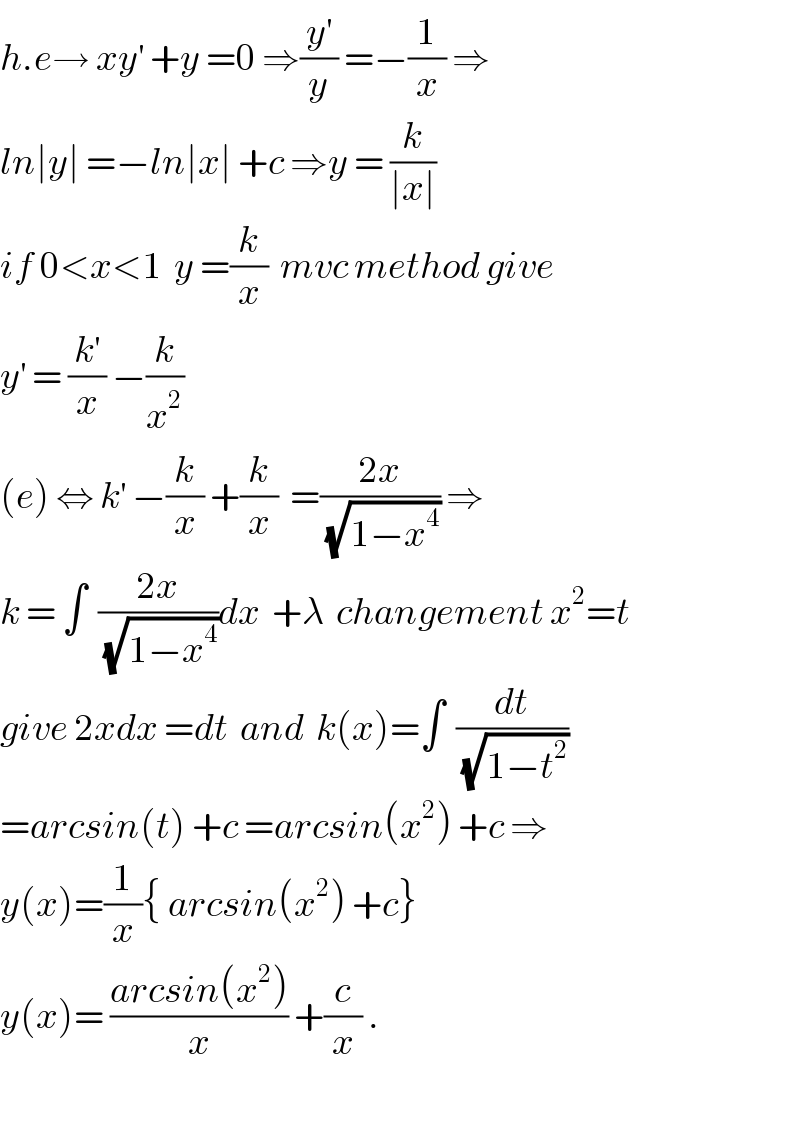
$${h}.{e}\rightarrow\:{xy}^{'} \:+{y}\:=\mathrm{0}\:\Rightarrow\frac{{y}^{'} }{{y}}\:=−\frac{\mathrm{1}}{{x}}\:\Rightarrow \\ $$$${ln}\mid{y}\mid\:=−{ln}\mid{x}\mid\:+{c}\:\Rightarrow{y}\:=\:\frac{{k}}{\mid{x}\mid} \\ $$$${if}\:\mathrm{0}<{x}<\mathrm{1}\:\:{y}\:=\frac{{k}}{{x}}\:\:{mvc}\:{method}\:{give} \\ $$$${y}^{'} \:=\:\frac{{k}^{'} }{{x}}\:−\frac{{k}}{{x}^{\mathrm{2}} } \\ $$$$\left({e}\right)\:\Leftrightarrow\:{k}^{'} \:−\frac{{k}}{{x}}\:+\frac{{k}}{{x}}\:\:=\frac{\mathrm{2}{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}\:\Rightarrow \\ $$$${k}\:=\:\int\:\:\frac{\mathrm{2}{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}{dx}\:\:+\lambda\:\:{changement}\:{x}^{\mathrm{2}} ={t} \\ $$$${give}\:\mathrm{2}{xdx}\:={dt}\:\:{and}\:\:{k}\left({x}\right)=\int\:\:\frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }} \\ $$$$={arcsin}\left({t}\right)\:+{c}\:={arcsin}\left({x}^{\mathrm{2}} \right)\:+{c}\:\Rightarrow \\ $$$${y}\left({x}\right)=\frac{\mathrm{1}}{{x}}\left\{\:{arcsin}\left({x}^{\mathrm{2}} \right)\:+{c}\right\}\: \\ $$$${y}\left({x}\right)=\:\frac{{arcsin}\left({x}^{\mathrm{2}} \right)}{{x}}\:+\frac{{c}}{{x}}\:. \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Jun/18
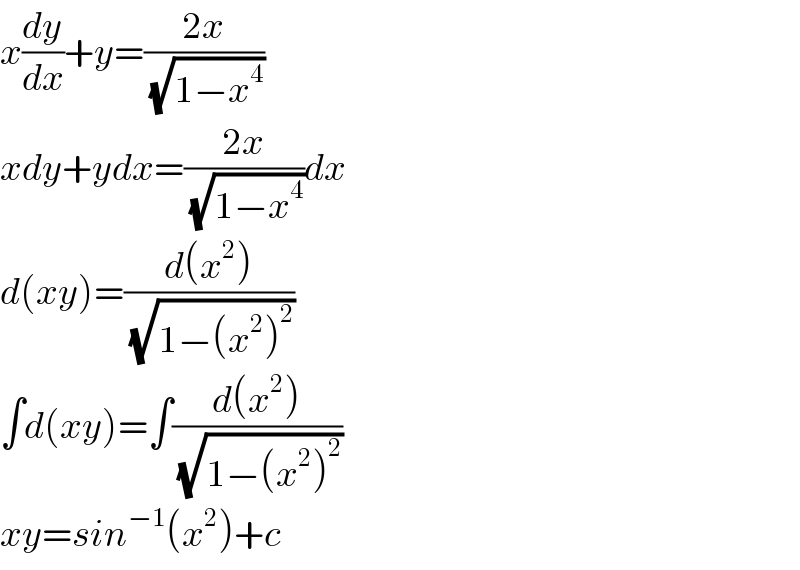
$${x}\frac{{dy}}{{dx}}+{y}=\frac{\mathrm{2}{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }} \\ $$$${xdy}+{ydx}=\frac{\mathrm{2}{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}{dx} \\ $$$${d}\left({xy}\right)=\frac{{d}\left({x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}−\left({x}^{\mathrm{2}} \right)^{\mathrm{2}} }} \\ $$$$\int{d}\left({xy}\right)=\int\frac{{d}\left({x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}−\left({x}^{\mathrm{2}} \right)^{\mathrm{2}} }} \\ $$$${xy}={sin}^{−\mathrm{1}} \left({x}^{\mathrm{2}} \right)+{c} \\ $$
