Menu Close

Integrate-the-following-1-a-x-x-dx-2-dx-sin-x-3-2-cos-x-

Tinku Tara 0 Comments
Pin




Question Number 84234 by niroj last updated on 10/Mar/20
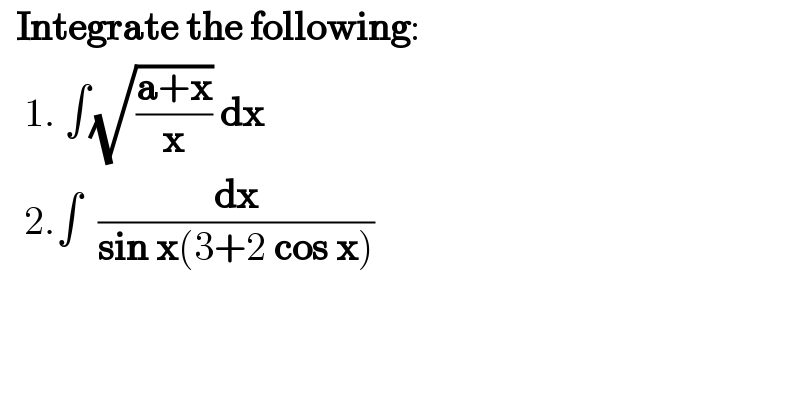
Integrate the following: 1. ∫(√((a+x)/x)) dx 2.∫ (dx/(sin x(3+2 cos x)))
$$\:\:\boldsymbol{\mathrm{Integrate}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{following}}: \\ $$$$\:\:\:\mathrm{1}.\:\int\sqrt{\frac{\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{x}}}{\boldsymbol{\mathrm{x}}}}\:\boldsymbol{\mathrm{dx}} \\ $$$$\:\:\:\mathrm{2}.\int\:\:\frac{\boldsymbol{\mathrm{dx}}}{\boldsymbol{\mathrm{sin}}\:\boldsymbol{\mathrm{x}}\left(\mathrm{3}+\mathrm{2}\:\boldsymbol{\mathrm{cos}}\:\boldsymbol{\mathrm{x}}\right)} \\ $$$$\: \\ $$
Commented by mathmax by abdo last updated on 10/Mar/20
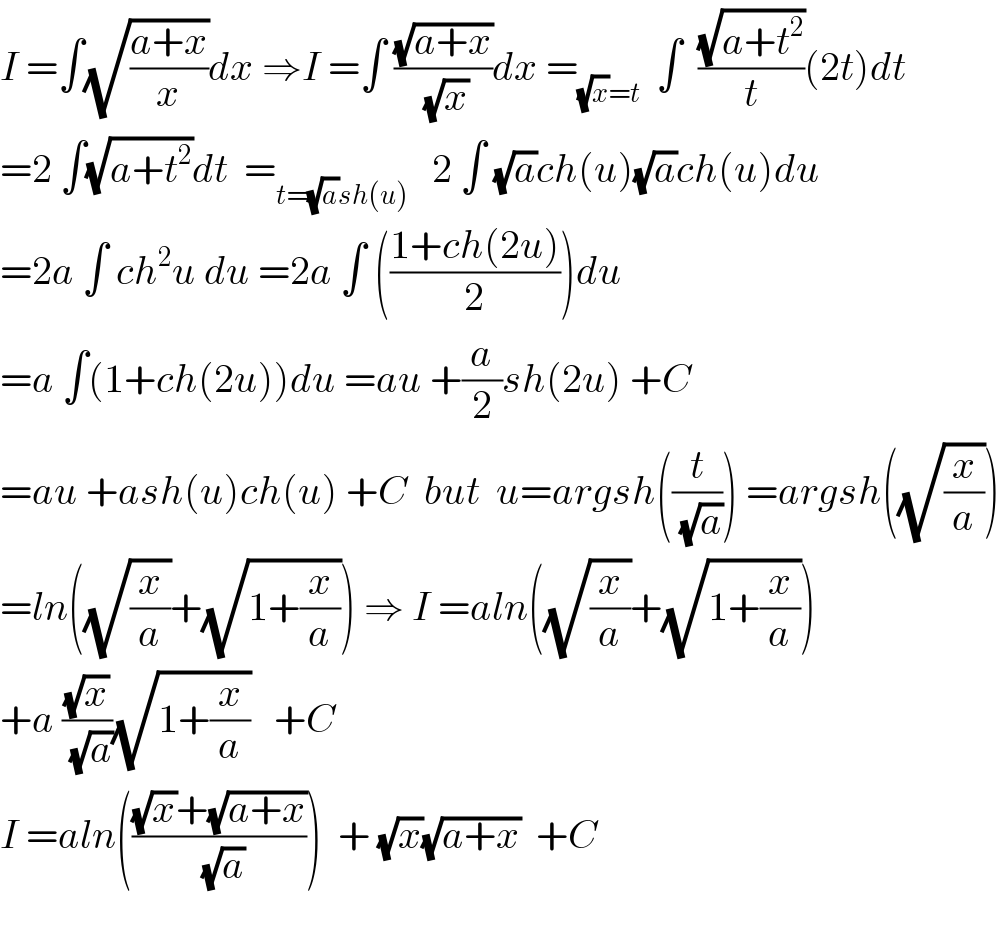
I =∫(√((a+x)/x))dx ⇒I =∫ ((√(a+x))/( (√x)))dx =_((√x)=t) ∫ ((√(a+t^2 ))/t)(2t)dt =2 ∫(√(a+t^2 ))dt =_(t=(√a)sh(u)) 2 ∫ (√a)ch(u)(√a)ch(u)du =2a ∫ ch^2 u du =2a ∫ (((1+ch(2u))/2))du =a ∫(1+ch(2u))du =au +(a/2)sh(2u) +C =au +ash(u)ch(u) +C but u=argsh((t/( (√a)))) =argsh((√(x/a))) =ln((√(x/a))+(√(1+(x/a)))) ⇒ I =aln((√(x/a))+(√(1+(x/a)))) +a ((√x)/( (√a)))(√(1+(x/a))) +C I =aln((((√x)+(√(a+x)))/( (√a)))) + (√x)(√(a+x)) +C
$${I}\:=\int\sqrt{\frac{{a}+{x}}{{x}}}{dx}\:\Rightarrow{I}\:=\int\:\frac{\sqrt{{a}+{x}}}{\:\sqrt{{x}}}{dx}\:=_{\sqrt{{x}}={t}} \:\:\int\:\:\frac{\sqrt{{a}+{t}^{\mathrm{2}} }}{{t}}\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\:\int\sqrt{{a}+{t}^{\mathrm{2}} }{dt}\:\:=_{{t}=\sqrt{{a}}{sh}\left({u}\right)} \:\:\:\mathrm{2}\:\int\:\sqrt{{a}}{ch}\left({u}\right)\sqrt{{a}}{ch}\left({u}\right){du} \\ $$$$=\mathrm{2}{a}\:\int\:{ch}^{\mathrm{2}} {u}\:{du}\:=\mathrm{2}{a}\:\int\:\left(\frac{\mathrm{1}+{ch}\left(\mathrm{2}{u}\right)}{\mathrm{2}}\right){du} \\ $$$$={a}\:\int\left(\mathrm{1}+{ch}\left(\mathrm{2}{u}\right)\right){du}\:={au}\:+\frac{{a}}{\mathrm{2}}{sh}\left(\mathrm{2}{u}\right)\:+{C} \\ $$$$={au}\:+{ash}\left({u}\right){ch}\left({u}\right)\:+{C}\:\:{but}\:\:{u}={argsh}\left(\frac{{t}}{\:\sqrt{{a}}}\right)\:={argsh}\left(\sqrt{\frac{{x}}{{a}}}\right) \\ $$$$={ln}\left(\sqrt{\frac{{x}}{{a}}}+\sqrt{\mathrm{1}+\frac{{x}}{{a}}}\right)\:\Rightarrow\:{I}\:={aln}\left(\sqrt{\frac{{x}}{{a}}}+\sqrt{\mathrm{1}+\frac{{x}}{{a}}}\right) \\ $$$$+{a}\:\frac{\sqrt{{x}}}{\:\sqrt{{a}}}\sqrt{\mathrm{1}+\frac{{x}}{{a}}}\:\:\:+{C} \\ $$$${I}\:={aln}\left(\frac{\sqrt{{x}}+\sqrt{{a}+{x}}}{\:\sqrt{{a}}}\right)\:\:+\:\sqrt{{x}}\sqrt{{a}+{x}}\:\:+{C} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 10/Mar/20
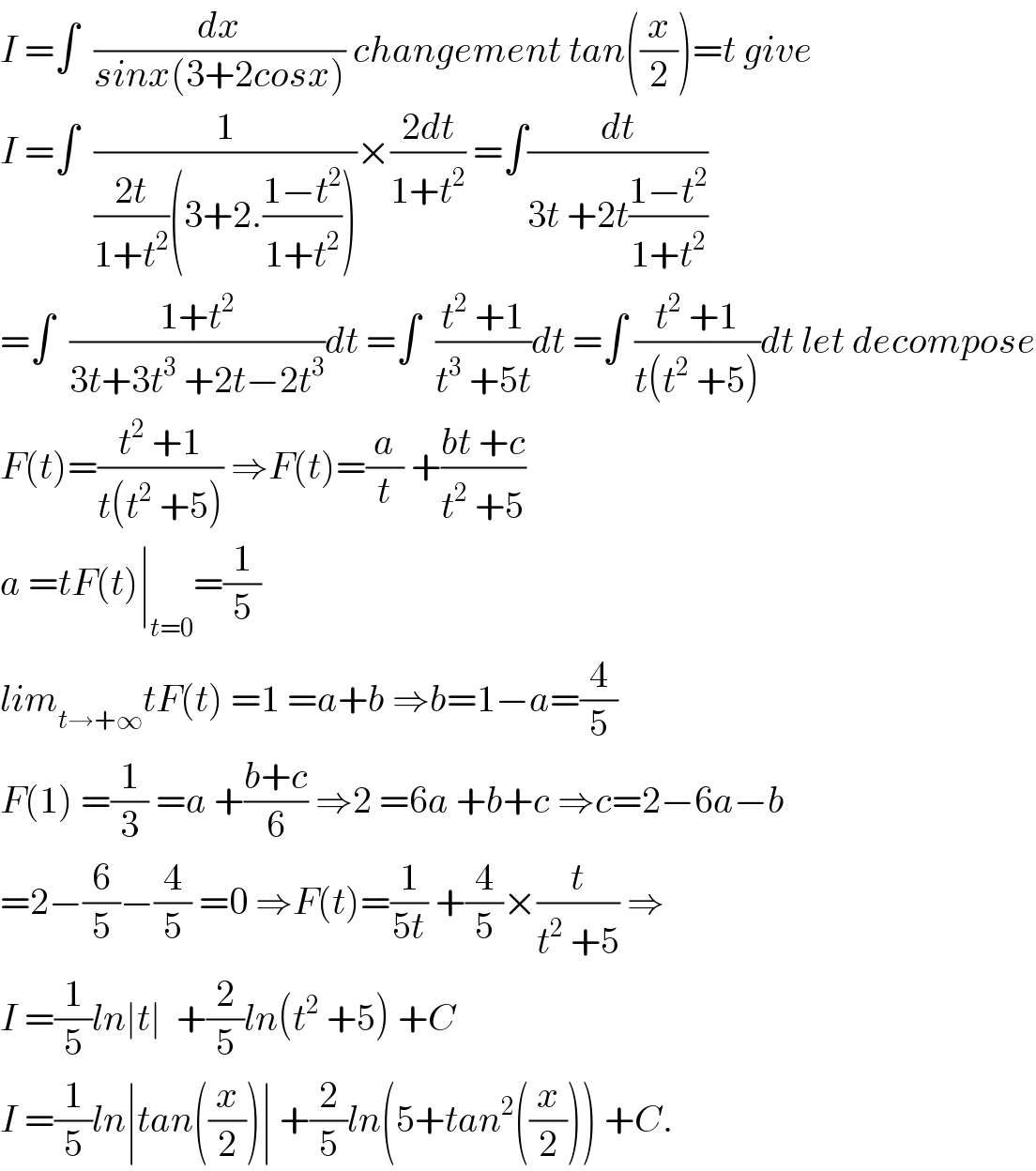
I =∫ (dx/(sinx(3+2cosx))) changement tan((x/2))=t give I =∫ (1/(((2t)/(1+t^2 ))(3+2.((1−t^2 )/(1+t^2 )))))×((2dt)/(1+t^2 )) =∫(dt/(3t +2t((1−t^2 )/(1+t^2 )))) =∫ ((1+t^2 )/(3t+3t^3 +2t−2t^3 ))dt =∫ ((t^2 +1)/(t^3 +5t))dt =∫ ((t^2 +1)/(t(t^2 +5)))dt let decompose F(t)=((t^2 +1)/(t(t^2 +5))) ⇒F(t)=(a/t) +((bt +c)/(t^2 +5)) a =tF(t)∣_(t=0) =(1/5) lim_(t→+∞) tF(t) =1 =a+b ⇒b=1−a=(4/5) F(1) =(1/3) =a +((b+c)/6) ⇒2 =6a +b+c ⇒c=2−6a−b =2−(6/5)−(4/5) =0 ⇒F(t)=(1/(5t)) +(4/5)×(t/(t^2 +5)) ⇒ I =(1/5)ln∣t∣ +(2/5)ln(t^2 +5) +C I =(1/5)ln∣tan((x/2))∣ +(2/5)ln(5+tan^2 ((x/2))) +C.
$${I}\:=\int\:\:\frac{{dx}}{{sinx}\left(\mathrm{3}+\mathrm{2}{cosx}\right)}\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$${I}\:=\int\:\:\frac{\mathrm{1}}{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\left(\mathrm{3}+\mathrm{2}.\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)}×\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\int\frac{{dt}}{\mathrm{3}{t}\:+\mathrm{2}{t}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$$$=\int\:\:\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{3}{t}+\mathrm{3}{t}^{\mathrm{3}} \:+\mathrm{2}{t}−\mathrm{2}{t}^{\mathrm{3}} }{dt}\:=\int\:\:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}^{\mathrm{3}} \:+\mathrm{5}{t}}{dt}\:=\int\:\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}\left({t}^{\mathrm{2}} \:+\mathrm{5}\right)}{dt}\:{let}\:{decompose} \\ $$$${F}\left({t}\right)=\frac{{t}^{\mathrm{2}} \:+\mathrm{1}}{{t}\left({t}^{\mathrm{2}} \:+\mathrm{5}\right)}\:\Rightarrow{F}\left({t}\right)=\frac{{a}}{{t}}\:+\frac{{bt}\:+{c}}{{t}^{\mathrm{2}} \:+\mathrm{5}} \\ $$$${a}\:={tF}\left({t}\right)\mid_{{t}=\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${lim}_{{t}\rightarrow+\infty} {tF}\left({t}\right)\:=\mathrm{1}\:={a}+{b}\:\Rightarrow{b}=\mathrm{1}−{a}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${F}\left(\mathrm{1}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}\:={a}\:+\frac{{b}+{c}}{\mathrm{6}}\:\Rightarrow\mathrm{2}\:=\mathrm{6}{a}\:+{b}+{c}\:\Rightarrow{c}=\mathrm{2}−\mathrm{6}{a}−{b} \\ $$$$=\mathrm{2}−\frac{\mathrm{6}}{\mathrm{5}}−\frac{\mathrm{4}}{\mathrm{5}}\:=\mathrm{0}\:\Rightarrow{F}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{5}{t}}\:+\frac{\mathrm{4}}{\mathrm{5}}×\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{5}}\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{5}}{ln}\mid{t}\mid\:\:+\frac{\mathrm{2}}{\mathrm{5}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{5}\right)\:+{C} \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{5}}{ln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)\mid\:+\frac{\mathrm{2}}{\mathrm{5}}{ln}\left(\mathrm{5}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)\:+{C}. \\ $$
Answered by TANMAY PANACEA last updated on 10/Mar/20
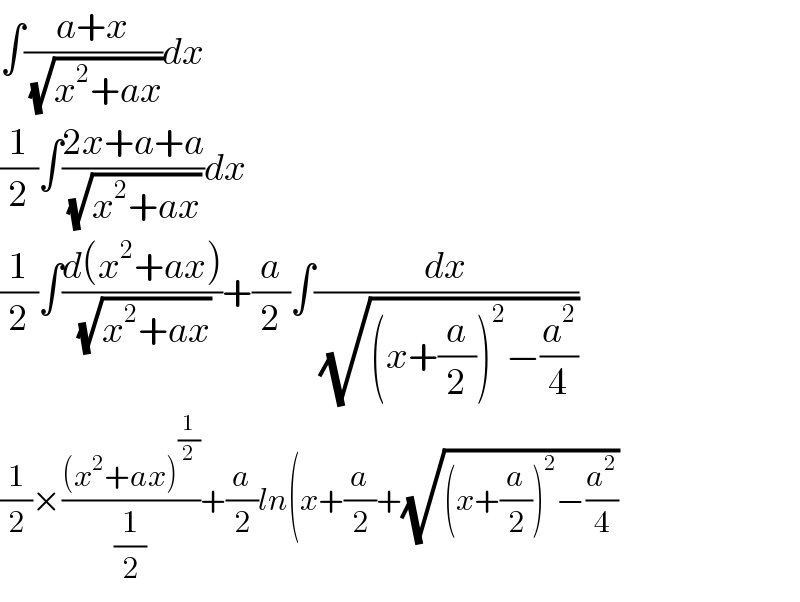
∫((a+x)/( (√(x^2 +ax))))dx (1/2)∫((2x+a+a)/( (√(x^2 +ax))))dx (1/2)∫((d(x^2 +ax))/( (√(x^2 +ax))))+(a/2)∫(dx/( (√((x+(a/2))^2 −(a^2 /4))))) (1/2)×(((x^2 +ax)^(1/2) )/(1/2))+(a/2)ln(x+(a/2)+(√((x+(a/2))^2 −(a^2 /4)))
$$\int\frac{{a}+{x}}{\:\sqrt{{x}^{\mathrm{2}} +{ax}}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{x}+{a}+{a}}{\:\sqrt{{x}^{\mathrm{2}} +{ax}}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}^{\mathrm{2}} +{ax}\right)}{\:\sqrt{{x}^{\mathrm{2}} +{ax}}}+\frac{{a}}{\mathrm{2}}\int\frac{{dx}}{\:\sqrt{\left({x}+\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\left({x}^{\mathrm{2}} +{ax}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{\frac{\mathrm{1}}{\mathrm{2}}}+\frac{{a}}{\mathrm{2}}{ln}\left({x}+\frac{{a}}{\mathrm{2}}+\sqrt{\left({x}+\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}}\:\right. \\ $$
Answered by TANMAY PANACEA last updated on 10/Mar/20
∫((sinx)/((1−cos^2 x)(3+2cosx)))dx ∫((−da)/((1−a^2 )(3+2a))) [a=cosx] ∫(da/((a+1)(a−1)(3+2a))) (1/((a+1)(a−1)(3+2a)))=(p/(a+1))+(q/(a−1))+(r/(3+2a)) 1=p(a−1)(3+2a)+q(a+1)(3+2a)+r(a+1)(a−1) put a−1=0 1=q×2×5→q=(1/(10)) put a+1=0 1=p(−2)(1)→p=((−1)/2) put 3+2a=0 1=r(((−3)/2)+1)(((−3)/2)−1)→1=r((5/4)) r=(4/5) ∫(((−1)/2)/(a+1))da+∫((1/(10))/(a−1))da+∫((4/5)/(3+2a))da ((−1)/2)ln(a+1)+(1/(10))ln(a−1)+(4/5)×(1/2)∫(da/(a+(3/2))) ((−1)/2)ln(cosx+1)+(1/(10))ln(cosx−1)+(4/(10))ln(cosx+(3/2))
$$\int\frac{{sinx}}{\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right)\left(\mathrm{3}+\mathrm{2}{cosx}\right)}{dx} \\ $$$$\int\frac{−{da}}{\left(\mathrm{1}−{a}^{\mathrm{2}} \right)\left(\mathrm{3}+\mathrm{2}{a}\right)}\:\:\:\left[{a}={cosx}\right] \\ $$$$\int\frac{{da}}{\left({a}+\mathrm{1}\right)\left({a}−\mathrm{1}\right)\left(\mathrm{3}+\mathrm{2}{a}\right)} \\ $$$$\frac{\mathrm{1}}{\left({a}+\mathrm{1}\right)\left({a}−\mathrm{1}\right)\left(\mathrm{3}+\mathrm{2}{a}\right)}=\frac{{p}}{{a}+\mathrm{1}}+\frac{{q}}{{a}−\mathrm{1}}+\frac{{r}}{\mathrm{3}+\mathrm{2}{a}} \\ $$$$\mathrm{1}={p}\left({a}−\mathrm{1}\right)\left(\mathrm{3}+\mathrm{2}{a}\right)+{q}\left({a}+\mathrm{1}\right)\left(\mathrm{3}+\mathrm{2}{a}\right)+{r}\left({a}+\mathrm{1}\right)\left({a}−\mathrm{1}\right) \\ $$$${put}\:{a}−\mathrm{1}=\mathrm{0}\:\: \\ $$$$\mathrm{1}={q}×\mathrm{2}×\mathrm{5}\rightarrow{q}=\frac{\mathrm{1}}{\mathrm{10}} \\ $$$${put}\:{a}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{1}={p}\left(−\mathrm{2}\right)\left(\mathrm{1}\right)\rightarrow{p}=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$$${put}\:\mathrm{3}+\mathrm{2}{a}=\mathrm{0} \\ $$$$\mathrm{1}={r}\left(\frac{−\mathrm{3}}{\mathrm{2}}+\mathrm{1}\right)\left(\frac{−\mathrm{3}}{\mathrm{2}}−\mathrm{1}\right)\rightarrow\mathrm{1}={r}\left(\frac{\mathrm{5}}{\mathrm{4}}\right)\:{r}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\int\frac{\frac{−\mathrm{1}}{\mathrm{2}}}{{a}+\mathrm{1}}{da}+\int\frac{\frac{\mathrm{1}}{\mathrm{10}}}{{a}−\mathrm{1}}{da}+\int\frac{\frac{\mathrm{4}}{\mathrm{5}}}{\mathrm{3}+\mathrm{2}{a}}{da} \\ $$$$\frac{−\mathrm{1}}{\mathrm{2}}{ln}\left({a}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{10}}{ln}\left({a}−\mathrm{1}\right)+\frac{\mathrm{4}}{\mathrm{5}}×\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{da}}{{a}+\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\frac{−\mathrm{1}}{\mathrm{2}}{ln}\left({cosx}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{10}}{ln}\left({cosx}−\mathrm{1}\right)+\frac{\mathrm{4}}{\mathrm{10}}{ln}\left({cosx}+\frac{\mathrm{3}}{\mathrm{2}}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by niroj last updated on 10/Mar/20
thanks for all to give your best.
$${thanks}\:{for}\:{all}\:{to}\:{give}\:{your}\:{best}. \\ $$
Answered by behi83417@gmail.com last updated on 04/Apr/20
∫(√((a+x)/x))dx [x=atg^2 t⇒dx=((2atgtdt)/(cos^2 t))] ⇒I=∫(1/(sint)).((2atgt)/(cos^2 t))dt=2a∫(dt/(cos^3 t))= =a[sect.tgt+ln(sect+tgt)]+C= =a[(√(x/a)).(√(1+(x/a)))+ln((√(1+(x/a)))+(√(x/a)))]= =(√(x^2 +ax))+a.ln((√(a+x))+(√x))+C′ . [tgt=(√(x/a)),sect=(√(1+tg^2 t))=(√(1+(x/a))),C′=C+(a/2)lna]
$$\int\sqrt{\frac{\mathrm{a}+\mathrm{x}}{\mathrm{x}}}\mathrm{dx}\:\:\:\:\left[\mathrm{x}=\mathrm{atg}^{\mathrm{2}} \mathrm{t}\Rightarrow\mathrm{dx}=\frac{\mathrm{2atgtdt}}{\mathrm{cos}^{\mathrm{2}} \mathrm{t}}\right] \\ $$$$\Rightarrow\mathrm{I}=\int\frac{\mathrm{1}}{\mathrm{sint}}.\frac{\mathrm{2atgt}}{\mathrm{cos}^{\mathrm{2}} \mathrm{t}}\mathrm{dt}=\mathrm{2a}\int\frac{\mathrm{dt}}{\mathrm{cos}^{\mathrm{3}} \mathrm{t}}= \\ $$$$=\mathrm{a}\left[\mathrm{sect}.\mathrm{tgt}+\mathrm{ln}\left(\mathrm{sect}+\mathrm{tgt}\right)\right]+\mathrm{C}= \\ $$$$=\mathrm{a}\left[\sqrt{\frac{\mathrm{x}}{\mathrm{a}}}.\sqrt{\mathrm{1}+\frac{\mathrm{x}}{\mathrm{a}}}+\mathrm{ln}\left(\sqrt{\mathrm{1}+\frac{\mathrm{x}}{\mathrm{a}}}+\sqrt{\frac{\mathrm{x}}{\mathrm{a}}}\right)\right]= \\ $$$$=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{ax}}+\mathrm{a}.\mathrm{ln}\left(\sqrt{\mathrm{a}+\mathrm{x}}+\sqrt{\mathrm{x}}\right)+\mathrm{C}'\:\:\:. \\ $$$$\left[\mathrm{tgt}=\sqrt{\frac{\mathrm{x}}{\mathrm{a}}},\mathrm{sect}=\sqrt{\mathrm{1}+\mathrm{tg}^{\mathrm{2}} \mathrm{t}}=\sqrt{\mathrm{1}+\frac{\mathrm{x}}{\mathrm{a}}},\mathrm{C}'=\mathrm{C}+\frac{\mathrm{a}}{\mathrm{2}}\mathrm{lna}\right] \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *