Question Number 124076 by TANMAY PANACEA last updated on 30/Nov/20

Commented by TANMAY PANACEA last updated on 30/Nov/20

Commented by TANMAY PANACEA last updated on 30/Nov/20

Commented by TANMAY PANACEA last updated on 30/Nov/20

Commented by TANMAY PANACEA last updated on 30/Nov/20

Commented by TANMAY PANACEA last updated on 30/Nov/20

Commented by TANMAY PANACEA last updated on 30/Nov/20

Commented by TANMAY PANACEA last updated on 30/Nov/20

Commented by TANMAY PANACEA last updated on 30/Nov/20

Commented by TANMAY PANACEA last updated on 30/Nov/20
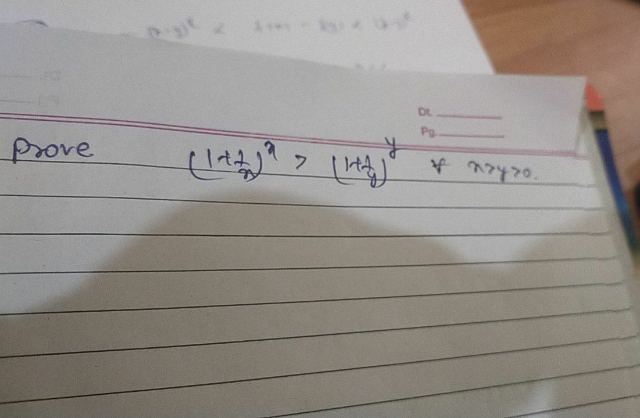
Commented by TANMAY PANACEA last updated on 30/Nov/20

Commented by TANMAY PANACEA last updated on 30/Nov/20

Commented by TANMAY PANACEA last updated on 30/Nov/20

Commented by Dwaipayan Shikari last updated on 30/Nov/20
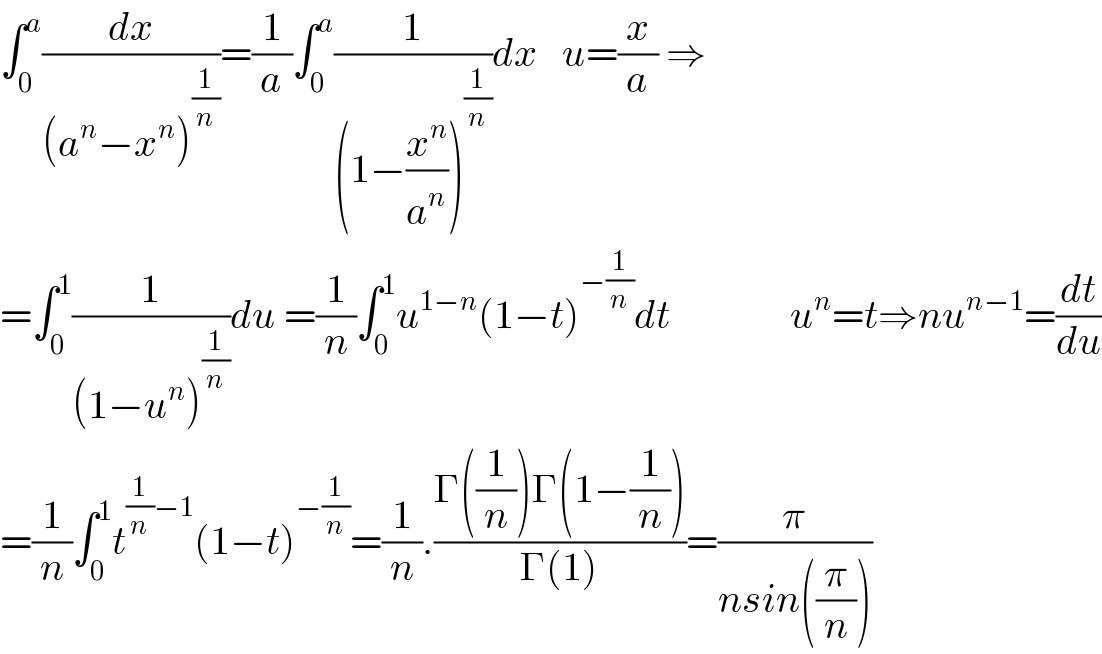
Commented by TANMAY PANACEA last updated on 30/Nov/20
Commented by mnjuly1970 last updated on 30/Nov/20
![note:: Γ(x)Γ(1−x)=(π/(sin(πx))) note:: ∫_0 ^( π) ln(sin(x))dx=−πln(2) Ω=∫_0 ^( 1) ln(Γ(x))dx Ω=∫_0 ^( 1) ln(Γ(1−x))dx 2Ω=∫_0 ^( 1) ln[(Γ(x)Γ(1−x))]dx 2Ω =^(euler reflection formula) ∫_0 ^( 1) ln((π/(sin(πx))))dx =ln(π)−∫_0 ^( 1) ln(sin(πx))dx =^(πx=t) ln(π)−(1/π)∫_0 ^( π) ln(sin(x))dx =ln(π)−(1/π)(−πln(2)) =ln(π)+ln(2)=ln(2π) ∴ Ω=(1/2)ln(2π)=ln((√(2π)) )✓](https://www.tinkutara.com/question/Q124097.png)
Commented by TANMAY PANACEA last updated on 30/Nov/20

Commented by mnjuly1970 last updated on 30/Nov/20
Commented by Dwaipayan Shikari last updated on 30/Nov/20
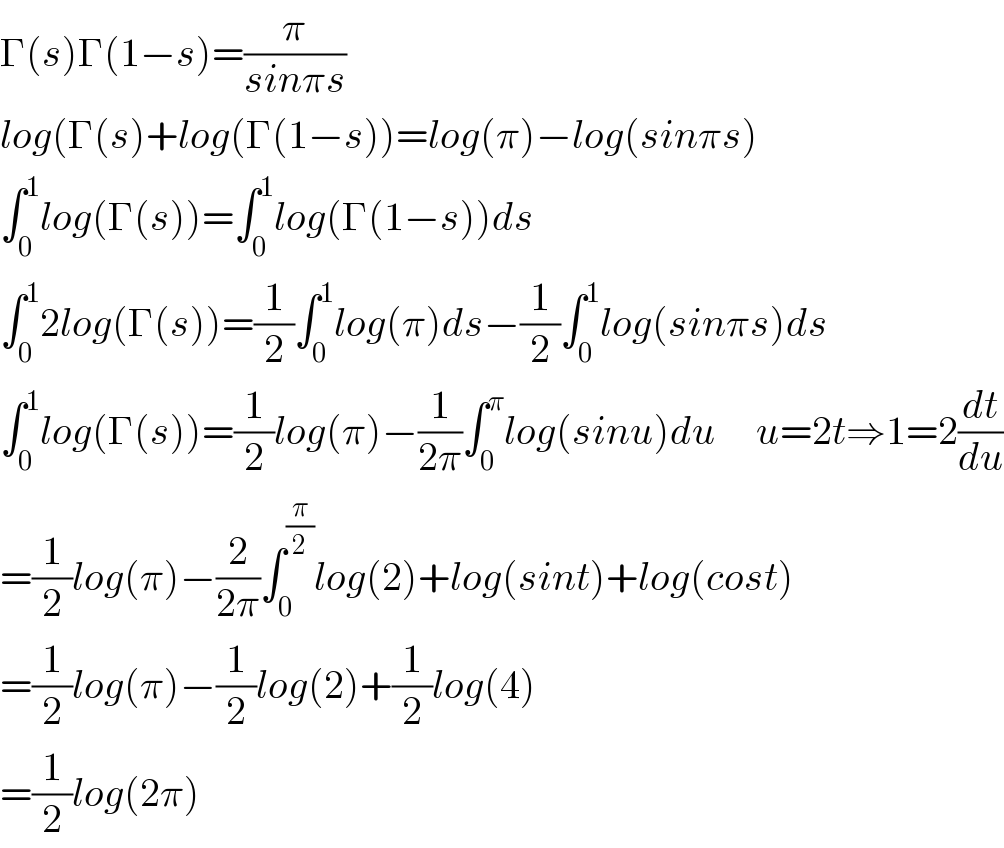
Commented by Dwaipayan Shikari last updated on 30/Nov/20

