Question Number 184920 by Mastermind last updated on 13/Jan/23
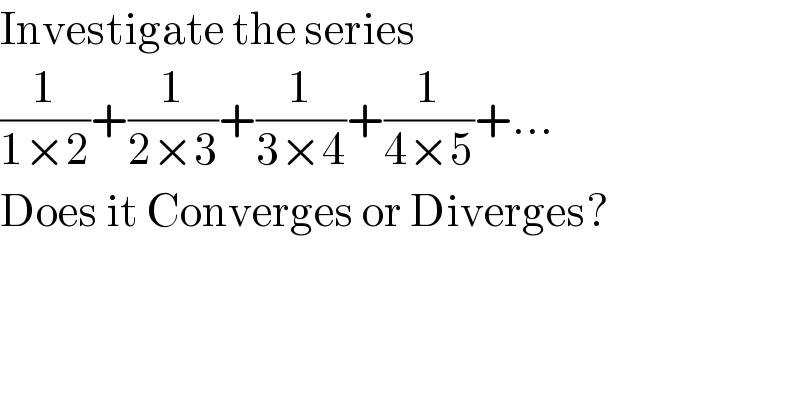
$$\mathrm{Investigate}\:\mathrm{the}\:\mathrm{series} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}×\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}×\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}×\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}×\mathrm{5}}+… \\ $$$$\mathrm{Does}\:\mathrm{it}\:\mathrm{Converges}\:\mathrm{or}\:\mathrm{Diverges}? \\ $$
Answered by aba last updated on 14/Jan/23
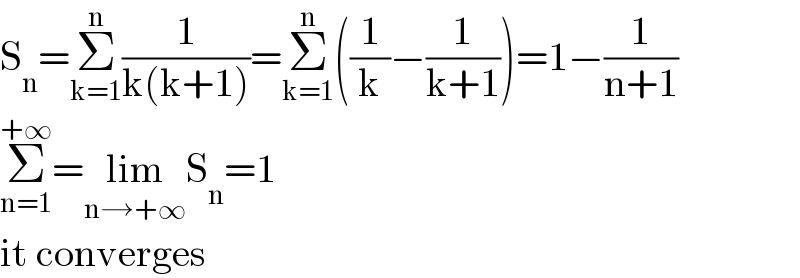
$$\mathrm{S}_{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)}=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}} \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{+\infty} {\sum}}=\underset{\mathrm{n}\rightarrow+\infty} {\mathrm{lim}S}_{\mathrm{n}} =\mathrm{1} \\ $$$$\mathrm{it}\:\mathrm{converges} \\ $$
