Question Number 93044 by fath035990 last updated on 10/May/20
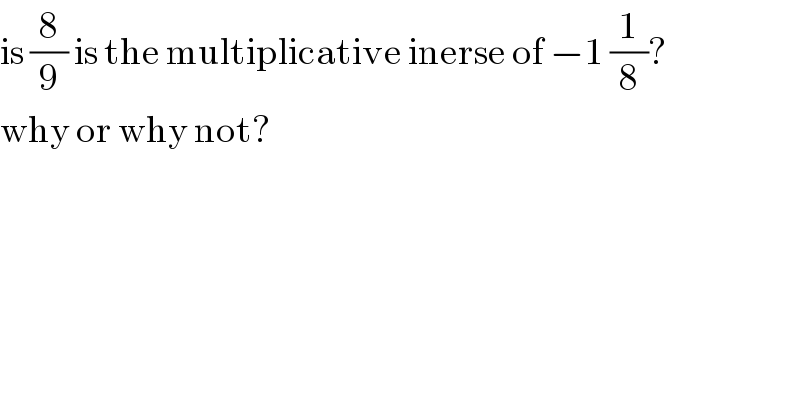
$$\mathrm{is}\:\frac{\mathrm{8}}{\mathrm{9}}\:\mathrm{is}\:\mathrm{the}\:\mathrm{multiplicative}\:\mathrm{inerse}\:\mathrm{of}\:−\mathrm{1}\:\frac{\mathrm{1}}{\mathrm{8}}? \\ $$$$\mathrm{why}\:\mathrm{or}\:\mathrm{why}\:\mathrm{not}? \\ $$
Commented by prakash jain last updated on 10/May/20
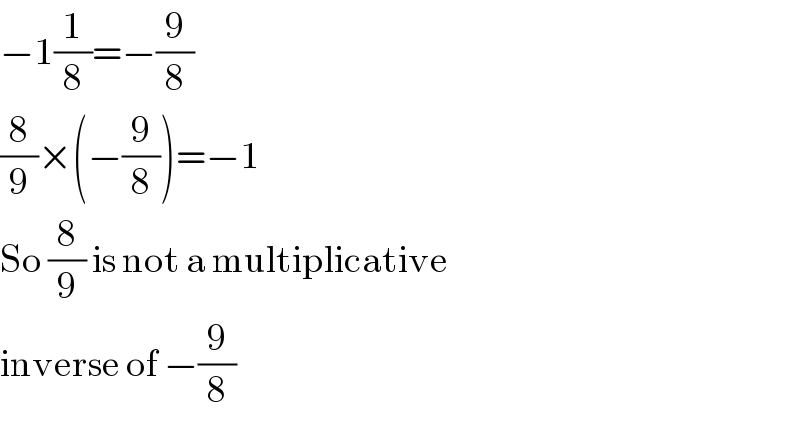
$$−\mathrm{1}\frac{\mathrm{1}}{\mathrm{8}}=−\frac{\mathrm{9}}{\mathrm{8}} \\ $$$$\frac{\mathrm{8}}{\mathrm{9}}×\left(−\frac{\mathrm{9}}{\mathrm{8}}\right)=−\mathrm{1} \\ $$$$\mathrm{So}\:\frac{\mathrm{8}}{\mathrm{9}}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{multiplicative} \\ $$$$\mathrm{inverse}\:\mathrm{of}\:−\frac{\mathrm{9}}{\mathrm{8}} \\ $$
Commented by fath035990 last updated on 10/May/20

$$\mathrm{thanks} \\ $$$$ \\ $$
Answered by Rio Michael last updated on 10/May/20
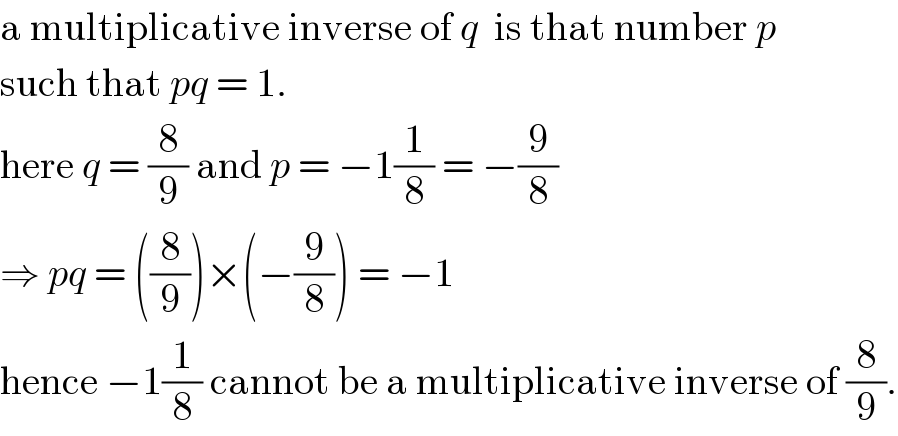
$$\mathrm{a}\:\mathrm{multiplicative}\:\mathrm{inverse}\:\mathrm{of}\:{q}\:\:\mathrm{is}\:\mathrm{that}\:\mathrm{number}\:{p}\: \\ $$$$\mathrm{such}\:\mathrm{that}\:{pq}\:=\:\mathrm{1}. \\ $$$$\mathrm{here}\:{q}\:=\:\frac{\mathrm{8}}{\mathrm{9}}\:\mathrm{and}\:{p}\:=\:−\mathrm{1}\frac{\mathrm{1}}{\mathrm{8}}\:=\:−\frac{\mathrm{9}}{\mathrm{8}} \\ $$$$\Rightarrow\:{pq}\:=\:\left(\frac{\mathrm{8}}{\mathrm{9}}\right)×\left(−\frac{\mathrm{9}}{\mathrm{8}}\right)\:=\:−\mathrm{1} \\ $$$$\mathrm{hence}\:−\mathrm{1}\frac{\mathrm{1}}{\mathrm{8}}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{a}\:\mathrm{multiplicative}\:\mathrm{inverse}\:\mathrm{of}\:\frac{\mathrm{8}}{\mathrm{9}}. \\ $$
