Is-a-complex-number-If-not-so-what-is-It-

Question Number 56244 by Kunal12588 last updated on 12/Mar/19

I s \infty a c o m p l e x n u m b e r .

I f n o t s o w h a t i s I t .

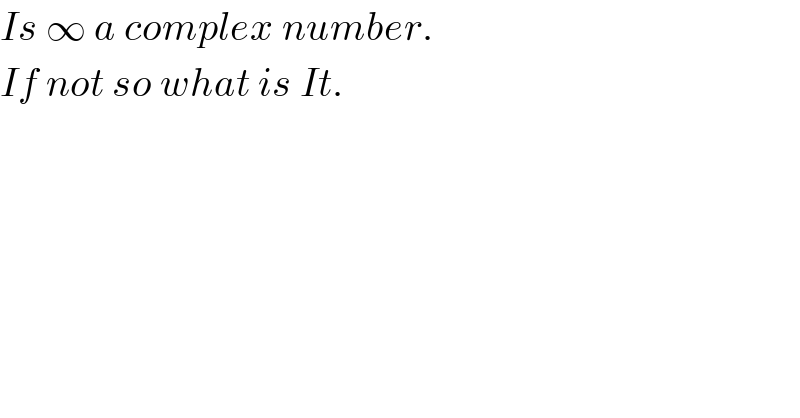
Commented by Joel578 last updated on 12/Mar/19

i t i s n o t a n u m b e r

Commented by Kunal12588 last updated on 12/Mar/19

o k i e d o k i e .

w a i t i n g f o r t h e n w h a t i t i s

a n d i t h o u g h t w e c a n r e p r e s e n t i t a s \frac{1}{0} .

s o \frac{1}{0} i s n o t a n u m b e r . b u t b o t h n u m e r a t o r

a n d d e n o m i n a t o r a r e n u m b e r s .

Commented by 121194 last updated on 12/Mar/19

one may think that \frac{1}{0} = \infty, but that not entire true

think of

\lim_{x \to 0} \frac{1}{x}

lets aproach it 2 ways

1 \to 1

0.5 \to 2

0.1 \to 10

0.01 \to 100

0.001 \to 1000

a s y o u c a n s e e a s c l o s e w e a p r o a c h x 1 / x g r o w

w i t h o u t a n y l i m i t, s o

\lim_{x \to 0^{+}} \frac{1}{x} = + \infty

b u t t h a t o n l y 1 p a t h, t a k e s t h e 2 n d o n e

- 1 \to - 1

- 0.5 \to - 2

- 0.1 \to - 10

- 0.01 \to - 100

a s y o u s e e i t g r o w i n c o m p l e t o p o s t d i r e c t i o n, a s

\lim_{x \to 0^{-}} \frac{1}{x} = - \infty

s i n c e t h e 2 l i m i t s a r e d i f e r e n t s w e {c a n}^{'} t s a y t h a t

t h e l i m i t e x i s t s o

\lim_{x \to 0} \frac{1}{x} = ∄

b t w t h e r e a n y a n a l o g o u s o f \infty t o c o m p l e x, t h e

c o m p l e x i n f i n i t e \tilde{\infty}

i t b a s i c a l y a “ {n u m b e r}^{″} w i t h h i g h m o d u l o s b u t

u n k n o w a r g u m e n t

Commented by Joel578 last updated on 12/Mar/19

\frac{1}{0} is actually undefined

Now, let f (x) = \frac{1}{x}

If we take x = 0.00000001, f (x) = 100000000

Next, if x getting smaller, very close to zero

then our f (x) is getting larger

Next, x now is very very very smaller, then

our f (x) is very very very large .

In this context, we can denote this as

\lim_{x \to 0^{+}} \frac{1}{x} = \frac{1}{0} = \infty

As x is getting smaller, very close to zero

then its value will reach an arbitrarily large number .

How large ? Very large . And we denote this with “ \infty^{″}

So, in my opinion “ \infty^{″} is a concept to describe

an arbitrarily large number, but it {isn}^{'} t a number

Commented by Joel578 last updated on 12/Mar/19

{That}^{'} s what I know . I am open for any critics if

I made any mistakes

Commented by Kunal12588 last updated on 12/Mar/19

t h a n k y o u v e r y m u c h s i r s .

Commented by prakash jain last updated on 12/Mar/19

please visit the below link for definition of complex infinity http://mathworld.wolfram.com/ComplexInfinity.html