Question Number 98895 by bramlex last updated on 17/Jun/20
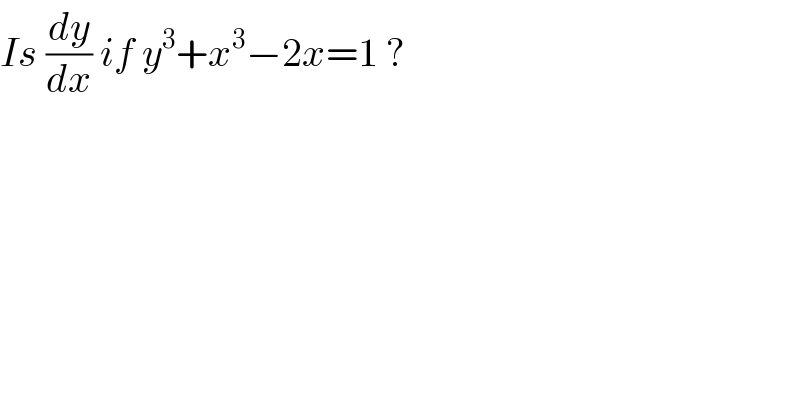
$${Is}\:\frac{{dy}}{{dx}}\:{if}\:{y}^{\mathrm{3}} +{x}^{\mathrm{3}} −\mathrm{2}{x}=\mathrm{1}\:?\: \\ $$
Answered by bramlex last updated on 17/Jun/20
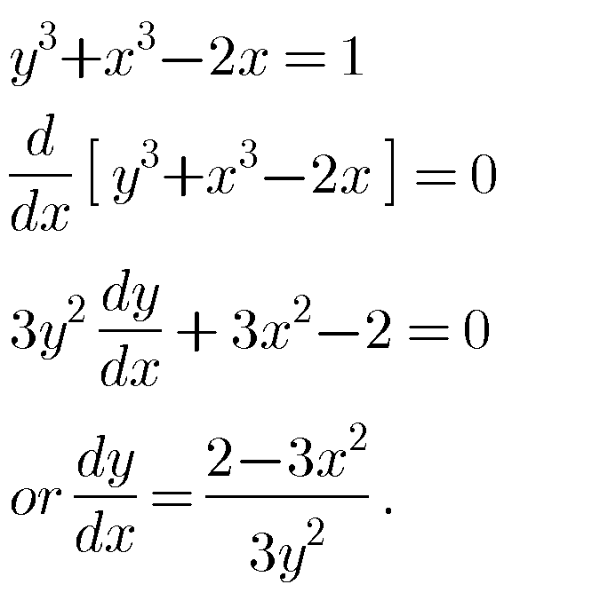
Answered by mathmax by abdo last updated on 17/Jun/20
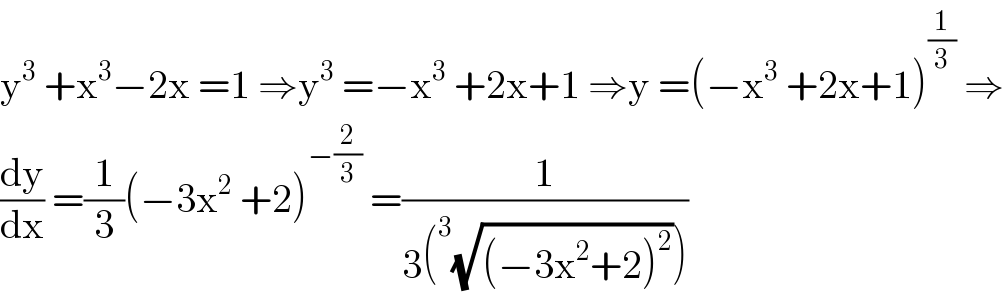
$$\mathrm{y}^{\mathrm{3}} \:+\mathrm{x}^{\mathrm{3}} −\mathrm{2x}\:=\mathrm{1}\:\Rightarrow\mathrm{y}^{\mathrm{3}} \:=−\mathrm{x}^{\mathrm{3}} \:+\mathrm{2x}+\mathrm{1}\:\Rightarrow\mathrm{y}\:=\left(−\mathrm{x}^{\mathrm{3}} \:+\mathrm{2x}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\Rightarrow \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\frac{\mathrm{1}}{\mathrm{3}}\left(−\mathrm{3x}^{\mathrm{2}} \:+\mathrm{2}\right)^{−\frac{\mathrm{2}}{\mathrm{3}}} \:=\frac{\mathrm{1}}{\mathrm{3}\left(^{\mathrm{3}} \sqrt{\left(−\mathrm{3x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }\right)} \\ $$
