is-it-possible-to-have-1-1-x-4-1-2-1-1-2x-4-please-help-

Question Number 120301 by TITA last updated on 30/Oct/20

i s i t p o s s i b l e t o h a v e {(1 + \frac{1}{x^{4}})}^{\frac{1}{2}} = (1 + \frac{1}{2 x^{4}}) p l e a s e h e l p

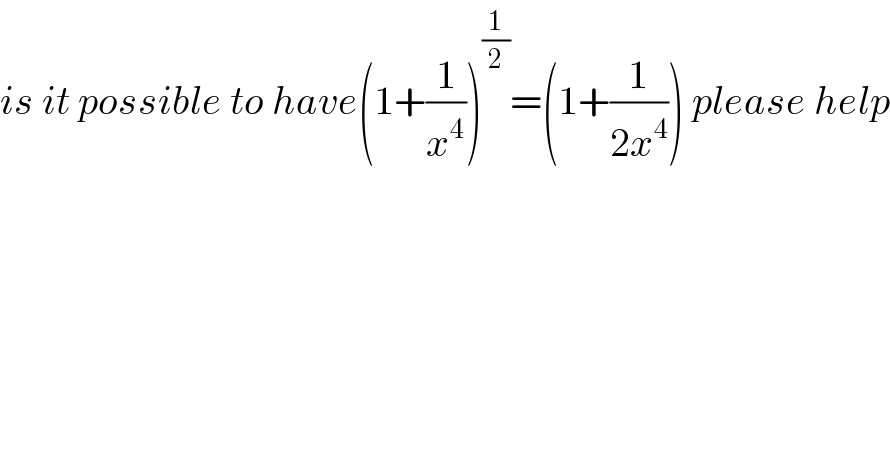
Commented by Dwaipayan Shikari last updated on 30/Oct/20

W h e n

x \to \infty

Commented by bemath last updated on 30/Oct/20

i n l i m i t i t i s p o s s i b l e .

\lim_{x \to 0} {(1 \pm f (x))}^{n} = \lim_{x \to 0} (1 \pm n f (x))

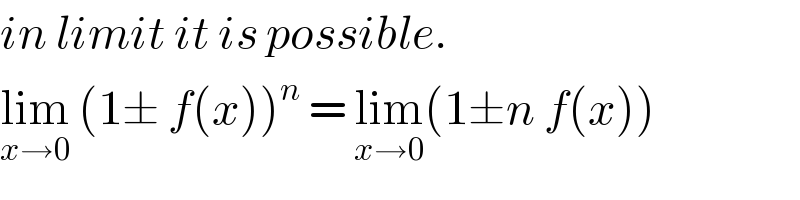
Commented by Bird last updated on 30/Oct/20

i f f (x) \to 0 w h e n x \to 0 w e g e t

{(1 + f (x))}^{n} \sim 1 + n f (x)

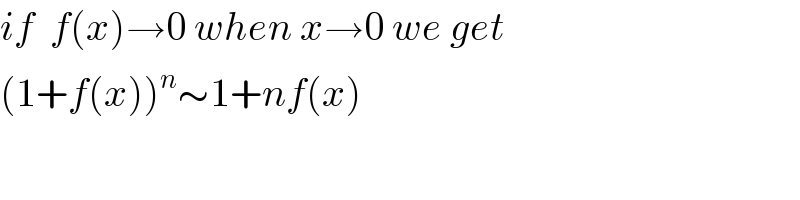
Answered by Bird last updated on 30/Oct/20

f o r x \to \infty (v e r y b i g v a l u e)

Facebook Tweet Pin