Question Number 63984 by Rio Michael last updated on 11/Jul/19
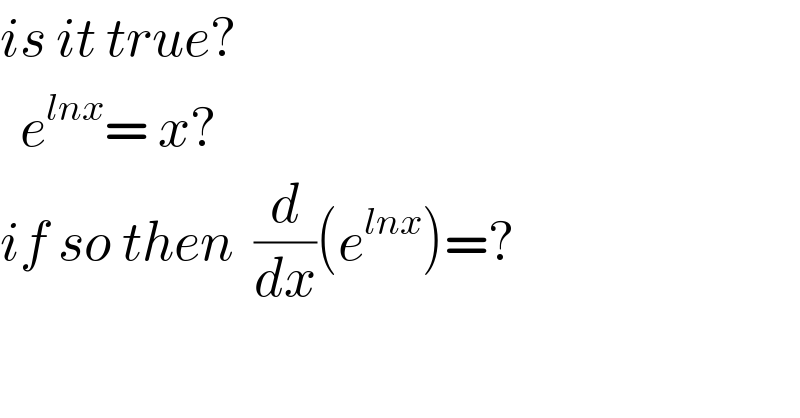
$${is}\:{it}\:{true}? \\ $$$$\:\:{e}^{{lnx}} =\:{x}? \\ $$$${if}\:{so}\:{then}\:\:\frac{{d}}{{dx}}\left({e}^{{lnx}} \right)=? \\ $$
Commented by mathmax by abdo last updated on 12/Jul/19
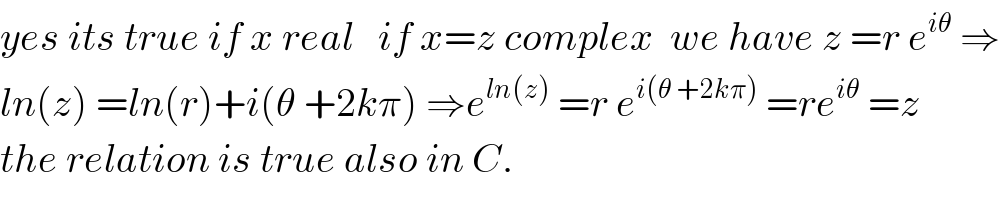
$${yes}\:{its}\:{true}\:{if}\:{x}\:{real}\:\:\:{if}\:{x}={z}\:{complex}\:\:{we}\:{have}\:{z}\:={r}\:{e}^{{i}\theta} \:\Rightarrow \\ $$$${ln}\left({z}\right)\:={ln}\left({r}\right)+{i}\left(\theta\:+\mathrm{2}{k}\pi\right)\:\Rightarrow{e}^{{ln}\left({z}\right)} \:={r}\:{e}^{{i}\left(\theta\:+\mathrm{2}{k}\pi\right)} \:={re}^{{i}\theta} \:={z} \\ $$$${the}\:{relation}\:{is}\:{true}\:{also}\:{in}\:{C}. \\ $$
Commented by mr W last updated on 11/Jul/19
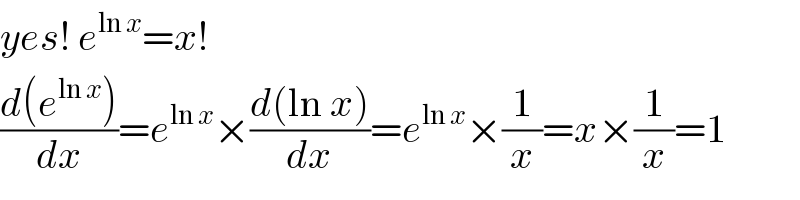
$${yes}!\:{e}^{\mathrm{ln}\:{x}} ={x}! \\ $$$$\frac{{d}\left({e}^{\mathrm{ln}\:{x}} \right)}{{dx}}={e}^{\mathrm{ln}\:{x}} ×\frac{{d}\left(\mathrm{ln}\:{x}\right)}{{dx}}={e}^{\mathrm{ln}\:{x}} ×\frac{\mathrm{1}}{{x}}={x}×\frac{\mathrm{1}}{{x}}=\mathrm{1} \\ $$
Commented by Rio Michael last updated on 11/Jul/19

$${nice}. \\ $$
Commented by kaivan.ahmadi last updated on 11/Jul/19
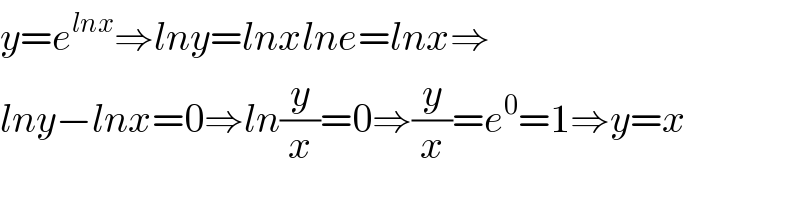
$${y}={e}^{{lnx}} \Rightarrow{lny}={lnxlne}={lnx}\Rightarrow \\ $$$${lny}−{lnx}=\mathrm{0}\Rightarrow{ln}\frac{{y}}{{x}}=\mathrm{0}\Rightarrow\frac{{y}}{{x}}={e}^{\mathrm{0}} =\mathrm{1}\Rightarrow{y}={x} \\ $$
Commented by kaivan.ahmadi last updated on 11/Jul/19
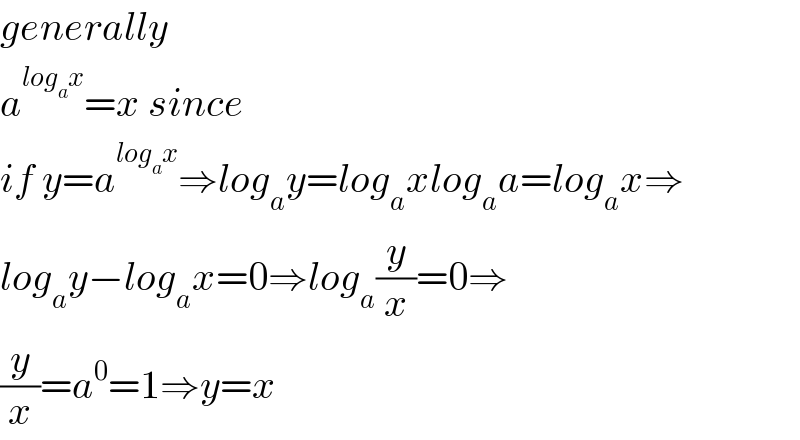
$${generally} \\ $$$${a}^{{log}_{{a}} {x}} ={x}\:{since} \\ $$$${if}\:{y}={a}^{{log}_{{a}} {x}} \Rightarrow{log}_{{a}} {y}={log}_{{a}} {xlog}_{{a}} {a}={log}_{{a}} {x}\Rightarrow \\ $$$${log}_{{a}} {y}−{log}_{{a}} {x}=\mathrm{0}\Rightarrow{log}_{{a}} \frac{{y}}{{x}}=\mathrm{0}\Rightarrow \\ $$$$\frac{{y}}{{x}}={a}^{\mathrm{0}} =\mathrm{1}\Rightarrow{y}={x} \\ $$
Answered by MJS last updated on 12/Jul/19

$${a}+{b}={c}\:\Leftrightarrow\:{a}={c}−{b}\:\Leftrightarrow\:{b}={c}−{a} \\ $$$$\mathrm{we}\:\mathrm{need}\:\mathrm{only}\:\mathrm{one}\:\mathrm{kind}\:\mathrm{of}\:\mathrm{operation} \\ $$$$\mathrm{same}\:\mathrm{here}: \\ $$$${a}×{b}={c}\:\Leftrightarrow\:{a}=\frac{{c}}{{b}}\:\Leftrightarrow\:{b}=\frac{{c}}{{a}} \\ $$$$\mathrm{that}'\mathrm{s}\:\mathrm{because}\:\mathrm{addition}\:\mathrm{and}\:\mathrm{multiplication} \\ $$$$\mathrm{both}\:\mathrm{are}\:\mathrm{commutative} \\ $$$${a}+{b}={b}+{c} \\ $$$${a}×{b}={b}×{a} \\ $$$$ \\ $$$$\mathrm{but} \\ $$$${a}^{{b}} \neq{b}^{{a}} \:\mathrm{in}\:\mathrm{general} \\ $$$${a}^{{b}} ={c}\:\Leftrightarrow\:{a}=\sqrt[{{b}}]{{c}}\:\Leftrightarrow\:{b}=\mathrm{log}_{{a}} \:{c} \\ $$$${a}^{{b}} =?\:\mathrm{with}\:{a}=\sqrt[{{b}}]{{c}} \\ $$$$\left(\sqrt[{{b}}]{{c}}\right)^{{b}} ={c} \\ $$$${a}^{{b}} =?\:\mathrm{with}\:{b}=\mathrm{log}_{{a}} \:{c} \\ $$$${a}^{\mathrm{log}_{{a}} \:{c}} ={c} \\ $$$$ \\ $$$$\mathrm{ln}\:{x}\:=\mathrm{log}_{\mathrm{e}} \:{x}\:\mathrm{but}\:\mathrm{some}\:\mathrm{people}\:\mathrm{use}\:\mathrm{log}\:{x}\:\mathrm{instead} \\ $$$$\mathrm{we}\:\mathrm{should}\:\mathrm{not}\:\mathrm{because}\:\mathrm{usually}\:\mathrm{log}\:{x}\:\mathrm{means} \\ $$$$\mathrm{log}_{\mathrm{10}} \:{x} \\ $$$$ \\ $$$$\mathrm{btw} \\ $$$$\mathrm{log}_{{a}} \:{b}\:=\frac{\mathrm{ln}\:{b}}{\mathrm{ln}\:{a}} \\ $$
Commented by Rio Michael last updated on 12/Jul/19
$${thanks}\:{so}\:{much} \\ $$
