Question Number 89576 by M±th+et£s last updated on 18/Apr/20
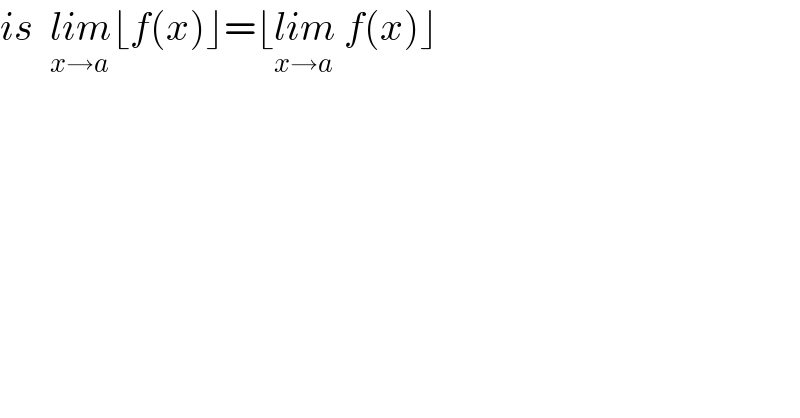
$${is}\:\:\underset{{x}\rightarrow{a}} {{lim}}\lfloor{f}\left({x}\right)\rfloor=\lfloor\underset{{x}\rightarrow{a}\:} {{lim}}\:{f}\left({x}\right)\rfloor\: \\ $$
Commented by mr W last updated on 18/Apr/20
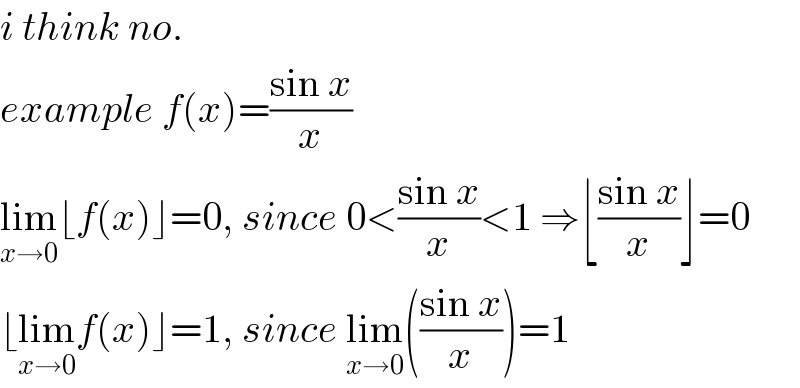
$${i}\:{think}\:{no}. \\ $$$${example}\:{f}\left({x}\right)=\frac{\mathrm{sin}\:{x}}{{x}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\lfloor{f}\left({x}\right)\rfloor=\mathrm{0},\:{since}\:\mathrm{0}<\frac{\mathrm{sin}\:{x}}{{x}}<\mathrm{1}\:\Rightarrow\lfloor\frac{\mathrm{sin}\:{x}}{{x}}\rfloor=\mathrm{0} \\ $$$$\lfloor\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}\left({x}\right)\rfloor=\mathrm{1},\:{since}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:{x}}{{x}}\right)=\mathrm{1} \\ $$
Commented by M±th+et£s last updated on 18/Apr/20
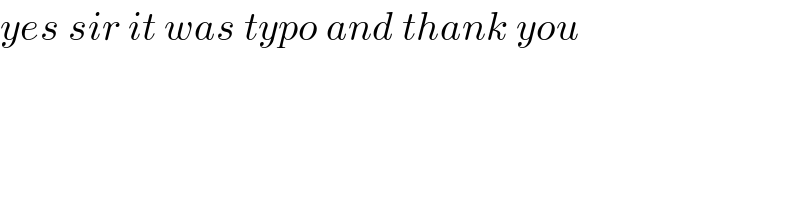
$${yes}\:{sir}\:{it}\:{was}\:{typo}\:{and}\:{thank}\:{you} \\ $$
Commented by mr W last updated on 18/Apr/20
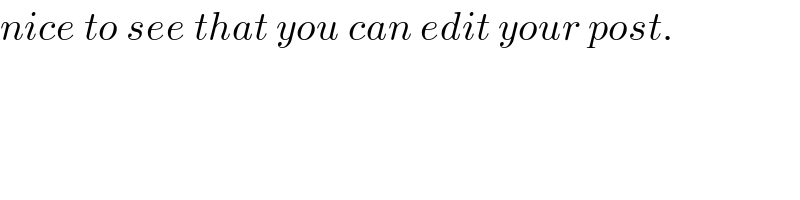
$${nice}\:{to}\:{see}\:{that}\:{you}\:{can}\:{edit}\:{your}\:{post}. \\ $$
