Is-tan-1-rational-or-irrational-Give-your-proof-

Question Number 54923 by mr W last updated on 14/Feb/19

$${Is}\:\mathrm{tan}\:\mathrm{1}°\:{rational}\:{or}\:{irrational}? \\ $$$${Give}\:{your}\:{proof}. \\ $$

Commented by Otchere Abdullai last updated on 14/Feb/19

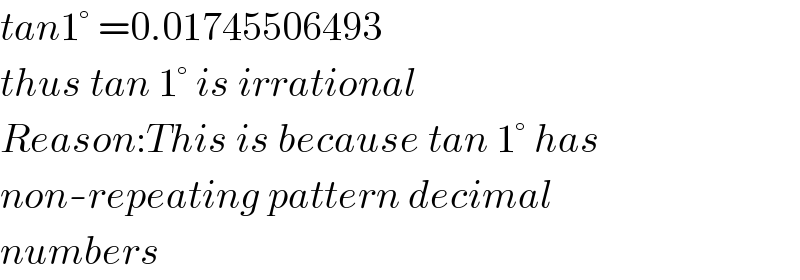
tan1° =0.01745506493 thus tan 1° is irrational Reason:This is because tan 1° has non-repeating pattern decimal numbers

$${tan}\mathrm{1}°\:=\mathrm{0}.\mathrm{01745506493} \\ $$$${thus}\:{tan}\:\mathrm{1}°\:{is}\:{irrational} \\ $$$${Reason}:{This}\:{is}\:{because}\:{tan}\:\mathrm{1}°\:{has} \\ $$$${non}-{repeating}\:{pattern}\:{decimal}\: \\ $$$${numbers} \\ $$

Commented by mr W last updated on 14/Feb/19

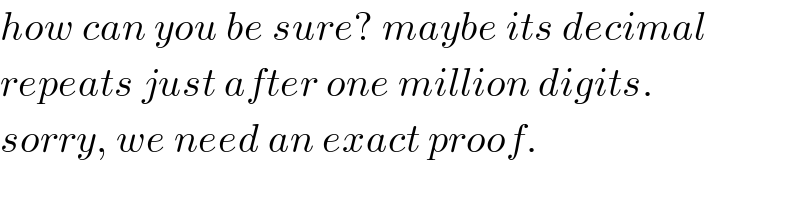
$${how}\:{can}\:{you}\:{be}\:{sure}?\:{maybe}\:{its}\:{decimal} \\ $$$${repeats}\:{just}\:{after}\:{one}\:{million}\:{digits}. \\ $$$${sorry},\:{we}\:{need}\:{an}\:{exact}\:{proof}. \\ $$

Commented by Otchere Abdullai last updated on 14/Feb/19

$${ok}\:{prof} \\ $$

Commented by Otchere Abdullai last updated on 15/Feb/19

step1. Assume that tan(1) is rational 2. therefore tan( 2) is rational 3.In general by induction tan(k) is rational 4. Tan(30) is rational 5. contradiction tan(1+1)=((tan(1)+tan(1))/(1−tan^2 (1)))∈Q tan(30)=(1/( (√3)))∉Q tan(k+1) =((tan(k)+tan(1))/(1−tan(k)tan(1)))∈Q ∴ tan1° is irrational

$${step}\mathrm{1}.\:{Assume}\:{that}\:{tan}\left(\mathrm{1}\right)\:{is}\:{rational} \\ $$$$\mathrm{2}.\:{therefore}\:{tan}\left(\:\mathrm{2}\right)\:{is}\:{rational} \\ $$$$\mathrm{3}.{In}\:{general}\:{by}\:{induction}\:{tan}\left({k}\right)\:{is} \\ $$$${rational} \\ $$$$\mathrm{4}.\:{Tan}\left(\mathrm{30}\right)\:{is}\:{rational} \\ $$$$\mathrm{5}.\:{contradiction} \\ $$$${tan}\left(\mathrm{1}+\mathrm{1}\right)=\frac{{tan}\left(\mathrm{1}\right)+{tan}\left(\mathrm{1}\right)}{\mathrm{1}−{tan}^{\mathrm{2}} \left(\mathrm{1}\right)}\in{Q} \\ $$$${tan}\left(\mathrm{30}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\notin{Q} \\ $$$${tan}\left({k}+\mathrm{1}\right)\:=\frac{{tan}\left({k}\right)+{tan}\left(\mathrm{1}\right)}{\mathrm{1}−{tan}\left({k}\right){tan}\left(\mathrm{1}\right)}\in{Q} \\ $$$$\therefore\:{tan}\mathrm{1}°\:{is}\:{irrational} \\ $$

Commented by mr W last updated on 15/Feb/19

$${thank}\:{you}\:{sir}!\:{good}\:{approach}! \\ $$

Commented by Otchere Abdullai last updated on 15/Feb/19

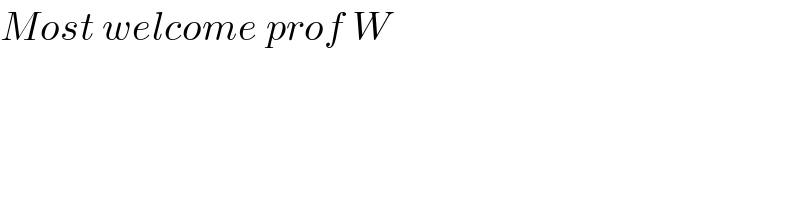
$${Most}\:{welcome}\:{prof}\:{W} \\ $$

Commented by $@ty@m last updated on 15/Feb/19

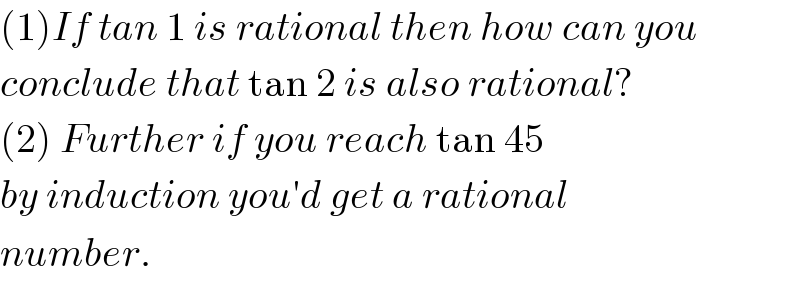
(1)If tan 1 is rational then how can you conclude that tan 2 is also rational? (2) Further if you reach tan 45 by induction you′d get a rational number.

$$\left(\mathrm{1}\right){If}\:{tan}\:\mathrm{1}\:{is}\:{rational}\:{then}\:{how}\:{can}\:{you} \\ $$$${conclude}\:{that}\:\mathrm{tan}\:\mathrm{2}\:{is}\:{also}\:{rational}? \\ $$$$\left(\mathrm{2}\right)\:{Further}\:{if}\:{you}\:{reach}\:\mathrm{tan}\:\mathrm{45} \\ $$$${by}\:{induction}\:{you}'{d}\:{get}\:{a}\:{rational} \\ $$$${number}.\: \\ $$

Commented by mr W last updated on 16/Feb/19

if tan 1° is rational, say tan 1°=(q/p) tan 2°=((2×(q/p))/(1−(q^2 /p^2 )))=((2pq)/((p−q)(p+q)))=(n/m) i.e. if tan 1° is rational, then ⇒tan 2° is also rational ⇒tan k° is also rational ⇒tan 45° is also rational (this is true) ⇒tan 60° is also rational (but this is not true) since tan k° is not always rational, it is not true that tan 1° is rational, in other words tan 1° must be irrational.

$${if}\:\mathrm{tan}\:\mathrm{1}°\:{is}\:{rational},\:{say}\:\mathrm{tan}\:\mathrm{1}°=\frac{{q}}{{p}} \\ $$$$\mathrm{tan}\:\mathrm{2}°=\frac{\mathrm{2}×\frac{{q}}{{p}}}{\mathrm{1}−\frac{{q}^{\mathrm{2}} }{{p}^{\mathrm{2}} }}=\frac{\mathrm{2}{pq}}{\left({p}−{q}\right)\left({p}+{q}\right)}=\frac{{n}}{{m}} \\ $$$${i}.{e}.\:{if}\:\mathrm{tan}\:\mathrm{1}°\:{is}\:{rational},\:{then} \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{2}°\:{is}\:{also}\:{rational} \\ $$$$\Rightarrow\mathrm{tan}\:{k}°\:{is}\:{also}\:{rational} \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{45}°\:{is}\:{also}\:{rational}\:\left({this}\:{is}\:{true}\right) \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{60}°\:{is}\:{also}\:{rational}\:\left({but}\:{this}\:{is}\:{not}\:{true}\right) \\ $$$${since}\:\mathrm{tan}\:{k}°\:{is}\:{not}\:{always}\:{rational}, \\ $$$${it}\:{is}\:{not}\:{true}\:{that}\:\mathrm{tan}\:\mathrm{1}°\:{is}\:{rational}, \\ $$$${in}\:{other}\:{words}\:\mathrm{tan}\:\mathrm{1}°\:{must}\:{be}\:{irrational}. \\ $$

Commented by $@ty@m last updated on 17/Feb/19

$${Thanks}\:{for}\:{clarification}. \\ $$

Facebook Tweet Pin

Is-tan-1-rational-or-irrational-Give-your-proof-

Leave a Reply Cancel reply