Menu Close

Is-there-any-other-solution-besides-x-a-y-b-or-x-b-y-a-of-the-following-system-of-equations-x-y-a-b-x-7-y-7-a-7-b-7-

Tinku Tara 0 Comments
Pin




Question Number 61470 by Rasheed.Sindhi last updated on 03/Jun/19
Is there any other solution besides {x=a,y=b} or {x=b,y=a} of the following system of equations x+y=a+b ∧ x^7 +y^7 =a^7 +b^7 ?
$$\mathrm{Is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{other}\:\mathrm{solution}\:\mathrm{besides} \\ $$$$\left\{\mathrm{x}=\mathrm{a},\mathrm{y}=\mathrm{b}\right\}\:\mathrm{or}\:\left\{\mathrm{x}=\mathrm{b},\mathrm{y}=\mathrm{a}\right\}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{following}\:\mathrm{system}\:\mathrm{of}\:\mathrm{equations} \\ $$$$\:\:\:\:\mathrm{x}+\mathrm{y}=\mathrm{a}+\mathrm{b}\:\:\wedge\:\mathrm{x}^{\mathrm{7}} +\mathrm{y}^{\mathrm{7}} =\mathrm{a}^{\mathrm{7}} +\mathrm{b}^{\mathrm{7}} \:\:? \\ $$$$ \\ $$
Answered by MJS last updated on 03/Jun/19
x+y=a+b ⇒ y=a+b−x x^7 +y^7 −a^7 −b^7 =0 with y=a+b−x leads to x^6 −3(a+b)x^5 +5(a+b)^2 x^4 −5(a+b)^3 x^3 +3(a+b)^4 x^2 −(a+b)^5 x+ab(a^2 +ab+b^2 )^2 =0 x=r+((a+b)/2) r^6 +((5(a+b)^2 )/4)r^4 +((3(a+b)^4 )/(16))r^2 −(((a−b)^2 (9a^4 +8a^3 b+14a^2 b^2 +8ab^3 +9b^4 ))/(64))=0 r=±(√s) s=t−((5(a+b)^2 )/(12)) t^3 −(((a+b)^4 )/3)t−(((2a^2 +ab+2b^2 )(a^4 −8a^3 b−9a^2 b^2 −8ab^3 +b^4 ))/(27))=0 we can always exactly solve this in C depending on the values of a and b we need Cardano′s or the trigonometric formula
$${x}+{y}={a}+{b}\:\Rightarrow\:{y}={a}+{b}−{x} \\ $$$${x}^{\mathrm{7}} +{y}^{\mathrm{7}} −{a}^{\mathrm{7}} −{b}^{\mathrm{7}} =\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{with}\:{y}={a}+{b}−{x}\:\mathrm{leads}\:\mathrm{to} \\ $$$${x}^{\mathrm{6}} −\mathrm{3}\left({a}+{b}\right){x}^{\mathrm{5}} +\mathrm{5}\left({a}+{b}\right)^{\mathrm{2}} {x}^{\mathrm{4}} −\mathrm{5}\left({a}+{b}\right)^{\mathrm{3}} {x}^{\mathrm{3}} +\mathrm{3}\left({a}+{b}\right)^{\mathrm{4}} {x}^{\mathrm{2}} −\left({a}+{b}\right)^{\mathrm{5}} {x}+{ab}\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{0} \\ $$$${x}={r}+\frac{{a}+{b}}{\mathrm{2}} \\ $$$${r}^{\mathrm{6}} +\frac{\mathrm{5}\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{4}}{r}^{\mathrm{4}} +\frac{\mathrm{3}\left({a}+{b}\right)^{\mathrm{4}} }{\mathrm{16}}{r}^{\mathrm{2}} −\frac{\left({a}−{b}\right)^{\mathrm{2}} \left(\mathrm{9}{a}^{\mathrm{4}} +\mathrm{8}{a}^{\mathrm{3}} {b}+\mathrm{14}{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{8}{ab}^{\mathrm{3}} +\mathrm{9}{b}^{\mathrm{4}} \right)}{\mathrm{64}}=\mathrm{0} \\ $$$${r}=\pm\sqrt{{s}} \\ $$$${s}={t}−\frac{\mathrm{5}\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{12}} \\ $$$${t}^{\mathrm{3}} −\frac{\left({a}+{b}\right)^{\mathrm{4}} }{\mathrm{3}}{t}−\frac{\left(\mathrm{2}{a}^{\mathrm{2}} +{ab}+\mathrm{2}{b}^{\mathrm{2}} \right)\left({a}^{\mathrm{4}} −\mathrm{8}{a}^{\mathrm{3}} {b}−\mathrm{9}{a}^{\mathrm{2}} {b}^{\mathrm{2}} −\mathrm{8}{ab}^{\mathrm{3}} +{b}^{\mathrm{4}} \right)}{\mathrm{27}}=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{always}\:\mathrm{exactly}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{in}\:\mathbb{C} \\ $$$$\mathrm{depending}\:\mathrm{on}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:{a}\:\mathrm{and}\:{b}\:\mathrm{we}\:\mathrm{need} \\ $$$$\mathrm{Cardano}'\mathrm{s}\:\mathrm{or}\:\mathrm{the}\:\mathrm{trigonometric}\:\mathrm{formula} \\ $$
Commented by Rasheed.Sindhi last updated on 03/Jun/19
Sir how many real solutions if a,b∈R?
$$\mathrm{Sir}\:\:\mathrm{how}\:\mathrm{many}\:\mathrm{real}\:\mathrm{solutions}\:\mathrm{if}\:\mathrm{a},\mathrm{b}\in\mathbb{R}? \\ $$
Commented by MJS last updated on 03/Jun/19
it seems we always get 2 real solutions a, b and 4 complex solutions if a, b ∈R ∧ a≠0∨b≠0
$$\mathrm{it}\:\mathrm{seems}\:\mathrm{we}\:\mathrm{always}\:\mathrm{get}\:\mathrm{2}\:\mathrm{real}\:\mathrm{solutions}\:{a},\:{b} \\ $$$$\mathrm{and}\:\mathrm{4}\:\mathrm{complex}\:\mathrm{solutions}\:\mathrm{if}\:{a},\:{b}\:\in\mathbb{R}\:\wedge\:{a}\neq\mathrm{0}\vee{b}\neq\mathrm{0} \\ $$
Commented by Rasheed.Sindhi last updated on 03/Jun/19
ThαnkS for an Xcelent answer!
$$\mathcal{T}{h}\alpha{nk}\mathcal{S}\:{for}\:{an}\:\mathcal{X}{celent}\:{answer}! \\ $$
Commented by Rasheed.Sindhi last updated on 03/Jun/19
Sir can we prove the above ?
$$\boldsymbol{\mathrm{Sir}}\:\mathrm{can}\:\mathrm{we}\:\mathrm{prove}\:\mathrm{the}\:\mathrm{above}\:? \\ $$
Commented by MJS last updated on 03/Jun/19
of course it′s even easier! x^6 −3(a+b)x^5 +5(a+b)^2 x^4 −5(a+b)^3 x^3 +3(a+b)^4 x^2 −(a+b)^5 x+ab(a^2 +ab+b^2 )^2 =0 this must be true for x=a∨x=b ⇒ x^4 −2(a+b)x^3 +(3a^2 +5ab+3b^2 )x^2 −(2a^3 +5a^2 b+5ab^2 +2b^3 )x+(a^4 +2a^3 b+3a^2 b^2 +2ab^3 +b^4 )=0 x=r+((a+b)/2) r^4 +((3a^2 +4ab+3b^2 )/2)r^2 +((9a^4 +8a^3 b+14a^2 b^2 +8ab^3 +9b^4 )/(16))=0 r=±(√s) s=t−((3a^2 +4ab+3b^2 )/4) t=±((√(ab(4a^2 +5ab+4b^2 )))/2) ⇒ s=−((3a^2 +4ab+3b^2 )/4)±((√(ab(4a^2 +5ab+4b^2 )))/2) ⇒ r=±(√(−((3a^2 +4ab+3b^2 )/4)±((√(ab(4a^2 +5ab+4b^2 )))/2))) ⇒ x=((a+b)/2)±(√(−((3a^2 +4ab+3b^2 )/4)±((√(ab(4a^2 +5ab+4b^2 )))/2)))
$$\mathrm{of}\:\mathrm{course}\:\mathrm{it}'\mathrm{s}\:\mathrm{even}\:\mathrm{easier}! \\ $$$${x}^{\mathrm{6}} −\mathrm{3}\left({a}+{b}\right){x}^{\mathrm{5}} +\mathrm{5}\left({a}+{b}\right)^{\mathrm{2}} {x}^{\mathrm{4}} −\mathrm{5}\left({a}+{b}\right)^{\mathrm{3}} {x}^{\mathrm{3}} +\mathrm{3}\left({a}+{b}\right)^{\mathrm{4}} {x}^{\mathrm{2}} −\left({a}+{b}\right)^{\mathrm{5}} {x}+{ab}\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{must}\:\mathrm{be}\:\mathrm{true}\:\mathrm{for}\:{x}={a}\vee{x}={b} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{4}} −\mathrm{2}\left({a}+{b}\right){x}^{\mathrm{3}} +\left(\mathrm{3}{a}^{\mathrm{2}} +\mathrm{5}{ab}+\mathrm{3}{b}^{\mathrm{2}} \right){x}^{\mathrm{2}} −\left(\mathrm{2}{a}^{\mathrm{3}} +\mathrm{5}{a}^{\mathrm{2}} {b}+\mathrm{5}{ab}^{\mathrm{2}} +\mathrm{2}{b}^{\mathrm{3}} \right){x}+\left({a}^{\mathrm{4}} +\mathrm{2}{a}^{\mathrm{3}} {b}+\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{2}{ab}^{\mathrm{3}} +{b}^{\mathrm{4}} \right)=\mathrm{0} \\ $$$${x}={r}+\frac{{a}+{b}}{\mathrm{2}} \\ $$$${r}^{\mathrm{4}} +\frac{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{4}{ab}+\mathrm{3}{b}^{\mathrm{2}} }{\mathrm{2}}{r}^{\mathrm{2}} +\frac{\mathrm{9}{a}^{\mathrm{4}} +\mathrm{8}{a}^{\mathrm{3}} {b}+\mathrm{14}{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\mathrm{8}{ab}^{\mathrm{3}} +\mathrm{9}{b}^{\mathrm{4}} }{\mathrm{16}}=\mathrm{0} \\ $$$${r}=\pm\sqrt{{s}} \\ $$$${s}={t}−\frac{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{4}{ab}+\mathrm{3}{b}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${t}=\pm\frac{\sqrt{{ab}\left(\mathrm{4}{a}^{\mathrm{2}} +\mathrm{5}{ab}+\mathrm{4}{b}^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$$$\Rightarrow\:{s}=−\frac{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{4}{ab}+\mathrm{3}{b}^{\mathrm{2}} }{\mathrm{4}}\pm\frac{\sqrt{{ab}\left(\mathrm{4}{a}^{\mathrm{2}} +\mathrm{5}{ab}+\mathrm{4}{b}^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$$$\Rightarrow\:{r}=\pm\sqrt{−\frac{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{4}{ab}+\mathrm{3}{b}^{\mathrm{2}} }{\mathrm{4}}\pm\frac{\sqrt{{ab}\left(\mathrm{4}{a}^{\mathrm{2}} +\mathrm{5}{ab}+\mathrm{4}{b}^{\mathrm{2}} \right)}}{\mathrm{2}}} \\ $$$$\Rightarrow\:{x}=\frac{{a}+{b}}{\mathrm{2}}\pm\sqrt{−\frac{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{4}{ab}+\mathrm{3}{b}^{\mathrm{2}} }{\mathrm{4}}\pm\frac{\sqrt{{ab}\left(\mathrm{4}{a}^{\mathrm{2}} +\mathrm{5}{ab}+\mathrm{4}{b}^{\mathrm{2}} \right)}}{\mathrm{2}}} \\ $$
Commented by MJS last updated on 03/Jun/19
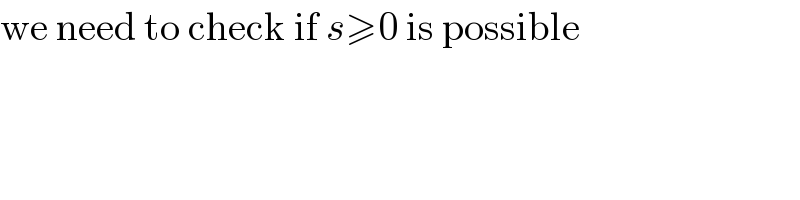
we need to check if s≥0 is possible
$$\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{check}\:\mathrm{if}\:{s}\geqslant\mathrm{0}\:\mathrm{is}\:\mathrm{possible} \\ $$
Commented by MJS last updated on 03/Jun/19
a∈R∧b∈R ⇒ t∈R
$${a}\in\mathbb{R}\wedge{b}\in\mathbb{R}\:\Rightarrow\:{t}\in\mathbb{R} \\ $$
Commented by MJS last updated on 03/Jun/19
s=−((3a^2 +4ab+3b^2 )/4)±((√(ab(4a^2 +5ab+4b^2 )))/2)≥ ? −((3a^2 +4ab+3b^2 )/4)±((√(ab(4a^2 +5ab+4b^2 )))/2)=0 (((3a^2 +4ab+3b^2 )/4))^2 =((ab(4a^2 +5ab+4b^2 ))/4) ⇒ a^4 +(8/9)a^3 b+((14)/9)a^2 b^2 +(8/9)ab^3 +b^4 =0 (a^2 +((2(2−(√(13))))/9)ab+b^2 )(a^2 +((2(2+(√(13))))/9)ab+b^2 )=0 no real linear factors ⇒ no change of sign(s) for a, b ∈R ⇒ s<0 ⇒ x∉R except x=a∨x=b
$${s}=−\frac{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{4}{ab}+\mathrm{3}{b}^{\mathrm{2}} }{\mathrm{4}}\pm\frac{\sqrt{{ab}\left(\mathrm{4}{a}^{\mathrm{2}} +\mathrm{5}{ab}+\mathrm{4}{b}^{\mathrm{2}} \right)}}{\mathrm{2}}\geqslant\:? \\ $$$$−\frac{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{4}{ab}+\mathrm{3}{b}^{\mathrm{2}} }{\mathrm{4}}\pm\frac{\sqrt{{ab}\left(\mathrm{4}{a}^{\mathrm{2}} +\mathrm{5}{ab}+\mathrm{4}{b}^{\mathrm{2}} \right)}}{\mathrm{2}}=\mathrm{0} \\ $$$$\left(\frac{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{4}{ab}+\mathrm{3}{b}^{\mathrm{2}} }{\mathrm{4}}\right)^{\mathrm{2}} =\frac{{ab}\left(\mathrm{4}{a}^{\mathrm{2}} +\mathrm{5}{ab}+\mathrm{4}{b}^{\mathrm{2}} \right)}{\mathrm{4}} \\ $$$$\Rightarrow \\ $$$${a}^{\mathrm{4}} +\frac{\mathrm{8}}{\mathrm{9}}{a}^{\mathrm{3}} {b}+\frac{\mathrm{14}}{\mathrm{9}}{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\frac{\mathrm{8}}{\mathrm{9}}{ab}^{\mathrm{3}} +{b}^{\mathrm{4}} =\mathrm{0} \\ $$$$\left({a}^{\mathrm{2}} +\frac{\mathrm{2}\left(\mathrm{2}−\sqrt{\mathrm{13}}\right)}{\mathrm{9}}{ab}+{b}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} +\frac{\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{13}}\right)}{\mathrm{9}}{ab}+{b}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\mathrm{no}\:\mathrm{real}\:\mathrm{linear}\:\mathrm{factors}\:\Rightarrow\:\mathrm{no}\:\mathrm{change}\:\mathrm{of}\:\mathrm{sign}\left({s}\right) \\ $$$$\mathrm{for}\:{a},\:{b}\:\in\mathbb{R}\:\Rightarrow\:{s}<\mathrm{0}\:\Rightarrow\:{x}\notin\mathbb{R}\:\mathrm{except}\:{x}={a}\vee{x}={b} \\ $$
Commented by Rasheed.Sindhi last updated on 03/Jun/19
ThαnkS a lot Sir! Actually your proof is required to me for solving Q#61273. Thanks again sir!
$$\mathcal{T}{h}\alpha{nk}\mathcal{S}\:{a}\:{lot}\:{Sir}! \\ $$$$\mathrm{Actually}\:\mathrm{your}\:\mathrm{proof}\:\mathrm{is}\:\mathrm{required}\:\mathrm{to} \\ $$$$\mathrm{me}\:\mathrm{for}\:\mathrm{solving}\:\mathrm{Q}#\mathrm{61273}. \\ $$$$\mathrm{Thanks}\:\mathrm{again}\:\mathrm{sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *