Menu Close

Is-there-any-solution-s-36x-2-y-27y-3-8-4x-3-27xy-2-4-please-

Tinku Tara 0 Comments
Pin




Question Number 123114 by nimnim last updated on 23/Nov/20
Is there any solution(s)?? { ((36x^2 y−27y^3 =8)),((4x^3 −27xy^2 =4)) :} please....
$${Is}\:{there}\:{any}\:{solution}\left({s}\right)?? \\ $$$$\begin{cases}{\mathrm{36}{x}^{\mathrm{2}} {y}−\mathrm{27}{y}^{\mathrm{3}} =\mathrm{8}}\\{\mathrm{4}{x}^{\mathrm{3}} −\mathrm{27}{xy}^{\mathrm{2}} =\mathrm{4}}\end{cases} \\ $$$${please}…. \\ $$
Commented by benjo_mathlover last updated on 23/Nov/20
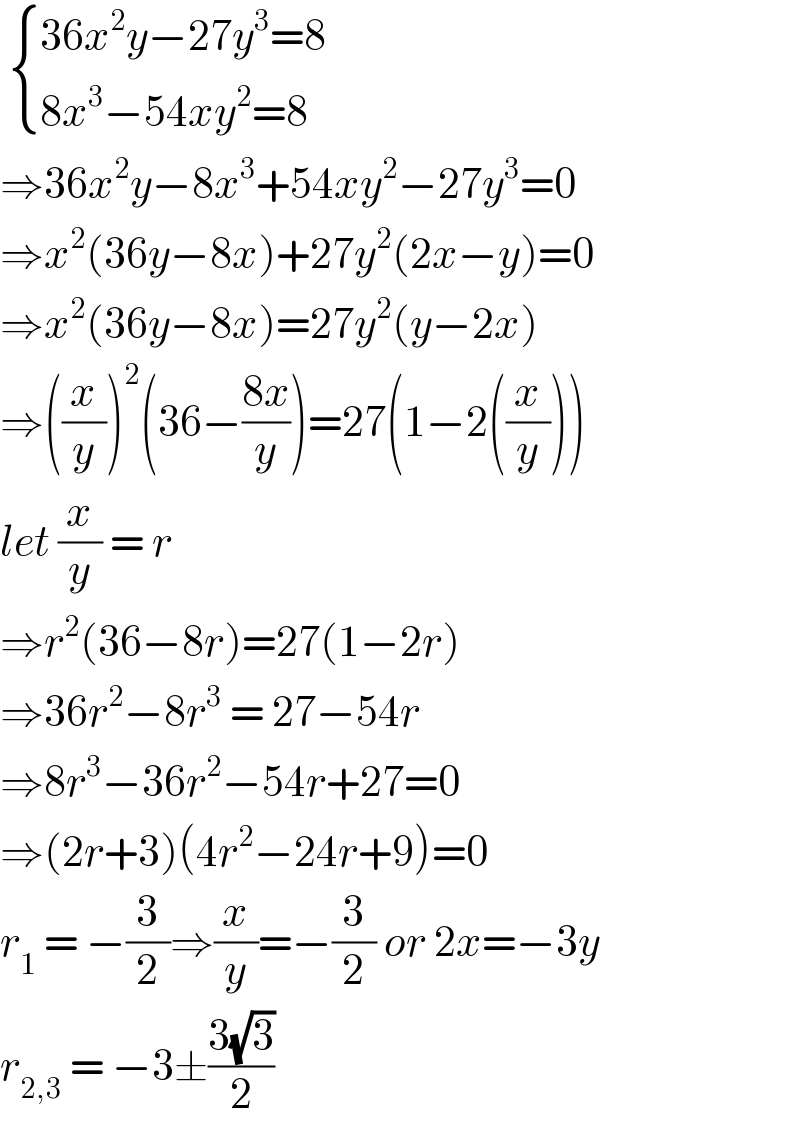
{ ((36x^2 y−27y^3 =8)),((8x^3 −54xy^2 =8)) :} ⇒36x^2 y−8x^3 +54xy^2 −27y^3 =0 ⇒x^2 (36y−8x)+27y^2 (2x−y)=0 ⇒x^2 (36y−8x)=27y^2 (y−2x) ⇒((x/y))^2 (36−((8x)/y))=27(1−2((x/y))) let (x/y) = r ⇒r^2 (36−8r)=27(1−2r) ⇒36r^2 −8r^3 = 27−54r ⇒8r^3 −36r^2 −54r+27=0 ⇒(2r+3)(4r^2 −24r+9)=0 r_1 = −(3/2)⇒(x/y)=−(3/2) or 2x=−3y r_(2,3) = −3±((3(√3))/2)
$$\:\begin{cases}{\mathrm{36}{x}^{\mathrm{2}} {y}−\mathrm{27}{y}^{\mathrm{3}} =\mathrm{8}}\\{\mathrm{8}{x}^{\mathrm{3}} −\mathrm{54}{xy}^{\mathrm{2}} =\mathrm{8}}\end{cases} \\ $$$$\Rightarrow\mathrm{36}{x}^{\mathrm{2}} {y}−\mathrm{8}{x}^{\mathrm{3}} +\mathrm{54}{xy}^{\mathrm{2}} −\mathrm{27}{y}^{\mathrm{3}} =\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} \left(\mathrm{36}{y}−\mathrm{8}{x}\right)+\mathrm{27}{y}^{\mathrm{2}} \left(\mathrm{2}{x}−{y}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} \left(\mathrm{36}{y}−\mathrm{8}{x}\right)=\mathrm{27}{y}^{\mathrm{2}} \left({y}−\mathrm{2}{x}\right) \\ $$$$\Rightarrow\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} \left(\mathrm{36}−\frac{\mathrm{8}{x}}{{y}}\right)=\mathrm{27}\left(\mathrm{1}−\mathrm{2}\left(\frac{{x}}{{y}}\right)\right) \\ $$$${let}\:\frac{{x}}{{y}}\:=\:{r}\: \\ $$$$\Rightarrow{r}^{\mathrm{2}} \left(\mathrm{36}−\mathrm{8}{r}\right)=\mathrm{27}\left(\mathrm{1}−\mathrm{2}{r}\right) \\ $$$$\Rightarrow\mathrm{36}{r}^{\mathrm{2}} −\mathrm{8}{r}^{\mathrm{3}} \:=\:\mathrm{27}−\mathrm{54}{r} \\ $$$$\Rightarrow\mathrm{8}{r}^{\mathrm{3}} −\mathrm{36}{r}^{\mathrm{2}} −\mathrm{54}{r}+\mathrm{27}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}{r}+\mathrm{3}\right)\left(\mathrm{4}{r}^{\mathrm{2}} −\mathrm{24}{r}+\mathrm{9}\right)=\mathrm{0} \\ $$$${r}_{\mathrm{1}} \:=\:−\frac{\mathrm{3}}{\mathrm{2}}\Rightarrow\frac{{x}}{{y}}=−\frac{\mathrm{3}}{\mathrm{2}}\:{or}\:\mathrm{2}{x}=−\mathrm{3}{y} \\ $$$${r}_{\mathrm{2},\mathrm{3}} \:=\:−\mathrm{3}\pm\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
Commented by nimnim last updated on 23/Nov/20
Thank you Sir.
$${Thank}\:{you}\:{Sir}. \\ $$
Answered by mindispower last updated on 23/Nov/20
⇔multiplie (1).i { ((36ix^2 y−27iy^3 =8i..(1))),((8x^3 −54xy^2 =8....(2))) :} and Eq 2 ∗2 (1)+(2)⇒−27iy^3 +8x^3 −54xy^2 +36ix^2 y=16 ⇔(3iy)^3 +(2x)^3 +3(3iy)^2 2+3(3iy)(2x)^2 =8(i+1) ⇔(3iy+2x)^3 =8(√2)e^(((iπ)/4)+i2kπ) ....x,y∈R this is suffisant to solve it if x,y∈C (1)∗−i+...(2)∗2 ⇒(−3iy)^3 +3(−3iy)(2x)^2 +(2x)^3 +3(−3iy)^2 .2x=−8i+8 ⇒(2x−3iy)^3 =8(1−i)=8(√2)e^(−((iπ)/4)+2k_1 π) ,k_1 ∈{0,1,2} ⇔ { ((2x−3iy=8(√2)e^(−i(π/(12))+2((ikπ)/3)) )),((2x+3iy=8(√2)e^(i(π/(12))+2((k_1 π)/3)) )) :} solve and theck evry solution because We used ⇒
$$\Leftrightarrow{multiplie}\:\left(\mathrm{1}\right).{i\begin{cases}{\mathrm{36}{ix}^{\mathrm{2}} {y}−\mathrm{27}{iy}^{\mathrm{3}} =\mathrm{8}{i}..\left(\mathrm{1}\right)}\\{\mathrm{8}{x}^{\mathrm{3}} −\mathrm{54}{xy}^{\mathrm{2}} =\mathrm{8}….\left(\mathrm{2}\right)}\end{cases}} \\ $$$${and}\:{Eq}\:\mathrm{2}\:\ast\mathrm{2} \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\Rightarrow−\mathrm{27}{iy}^{\mathrm{3}} +\mathrm{8}{x}^{\mathrm{3}} −\mathrm{54}{xy}^{\mathrm{2}} +\mathrm{36}{ix}^{\mathrm{2}} {y}=\mathrm{16} \\ $$$$\Leftrightarrow\left(\mathrm{3}{iy}\right)^{\mathrm{3}} +\left(\mathrm{2}{x}\right)^{\mathrm{3}} +\mathrm{3}\left(\mathrm{3}{iy}\right)^{\mathrm{2}} \mathrm{2}+\mathrm{3}\left(\mathrm{3}{iy}\right)\left(\mathrm{2}{x}\right)^{\mathrm{2}} =\mathrm{8}\left({i}+\mathrm{1}\right) \\ $$$$\Leftrightarrow\left(\mathrm{3}{iy}+\mathrm{2}{x}\right)^{\mathrm{3}} =\mathrm{8}\sqrt{\mathrm{2}}{e}^{\frac{{i}\pi}{\mathrm{4}}+{i}\mathrm{2}{k}\pi} ….{x},{y}\in\mathbb{R} \\ $$$${this}\:{is}\:{suffisant}\:{to}\:{solve}\:{it} \\ $$$${if}\:{x},{y}\in\mathbb{C} \\ $$$$\left(\mathrm{1}\right)\ast−{i}+…\left(\mathrm{2}\right)\ast\mathrm{2} \\ $$$$\Rightarrow\left(−\mathrm{3}{iy}\right)^{\mathrm{3}} +\mathrm{3}\left(−\mathrm{3}{iy}\right)\left(\mathrm{2}{x}\right)^{\mathrm{2}} +\left(\mathrm{2}{x}\right)^{\mathrm{3}} +\mathrm{3}\left(−\mathrm{3}{iy}\right)^{\mathrm{2}} .\mathrm{2}{x}=−\mathrm{8}{i}+\mathrm{8} \\ $$$$\Rightarrow\left(\mathrm{2}{x}−\mathrm{3}{iy}\right)^{\mathrm{3}} =\mathrm{8}\left(\mathrm{1}−{i}\right)=\mathrm{8}\sqrt{\mathrm{2}}{e}^{−\frac{{i}\pi}{\mathrm{4}}+\mathrm{2}{k}_{\mathrm{1}} \pi} ,{k}_{\mathrm{1}} \in\left\{\mathrm{0},\mathrm{1},\mathrm{2}\right\} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{2}{x}−\mathrm{3}{iy}=\mathrm{8}\sqrt{\mathrm{2}}{e}^{−{i}\frac{\pi}{\mathrm{12}}+\mathrm{2}\frac{{ik}\pi}{\mathrm{3}}} }\\{\mathrm{2}{x}+\mathrm{3}{iy}=\mathrm{8}\sqrt{\mathrm{2}}{e}^{{i}\frac{\pi}{\mathrm{12}}+\mathrm{2}\frac{{k}_{\mathrm{1}} \pi}{\mathrm{3}}} }\end{cases} \\ $$$${solve}\:{and}\:{theck}\:{evry}\:{solution}\:{because}\:{We} \\ $$$${used}\:\Rightarrow \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by nimnim last updated on 23/Nov/20
Thank you Sir.
$${Thank}\:{you}\:{Sir}. \\ $$
Answered by MJS_new last updated on 23/Nov/20
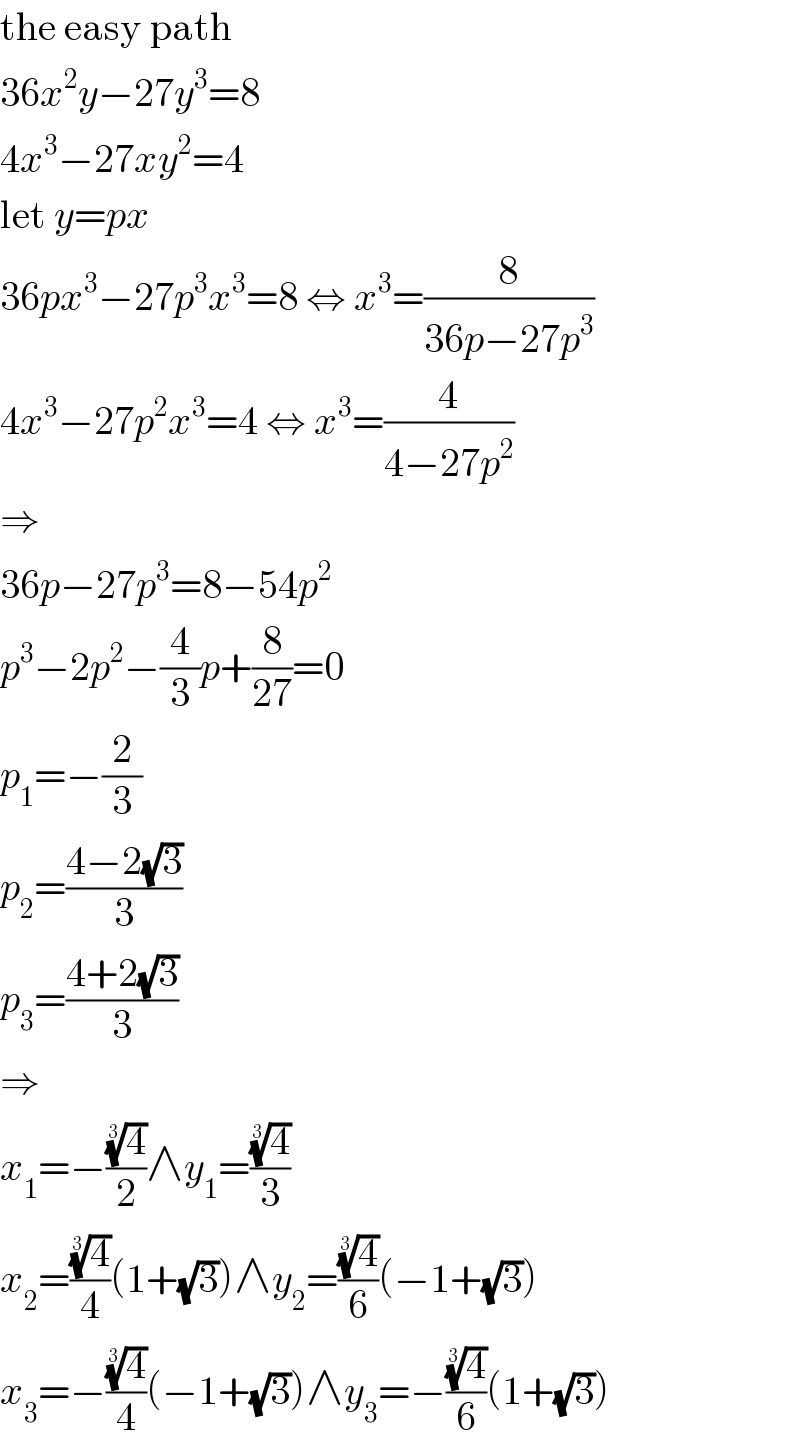
the easy path 36x^2 y−27y^3 =8 4x^3 −27xy^2 =4 let y=px 36px^3 −27p^3 x^3 =8 ⇔ x^3 =(8/(36p−27p^3 )) 4x^3 −27p^2 x^3 =4 ⇔ x^3 =(4/(4−27p^2 )) ⇒ 36p−27p^3 =8−54p^2 p^3 −2p^2 −(4/3)p+(8/(27))=0 p_1 =−(2/3) p_2 =((4−2(√3))/3) p_3 =((4+2(√3))/3) ⇒ x_1 =−((4)^(1/3) /2)∧y_1 =((4)^(1/3) /3) x_2 =((4)^(1/3) /4)(1+(√3))∧y_2 =((4)^(1/3) /6)(−1+(√3)) x_3 =−((4)^(1/3) /4)(−1+(√3))∧y_3 =−((4)^(1/3) /6)(1+(√3))
$$\mathrm{the}\:\mathrm{easy}\:\mathrm{path} \\ $$$$\mathrm{36}{x}^{\mathrm{2}} {y}−\mathrm{27}{y}^{\mathrm{3}} =\mathrm{8} \\ $$$$\mathrm{4}{x}^{\mathrm{3}} −\mathrm{27}{xy}^{\mathrm{2}} =\mathrm{4} \\ $$$$\mathrm{let}\:{y}={px} \\ $$$$\mathrm{36}{px}^{\mathrm{3}} −\mathrm{27}{p}^{\mathrm{3}} {x}^{\mathrm{3}} =\mathrm{8}\:\Leftrightarrow\:{x}^{\mathrm{3}} =\frac{\mathrm{8}}{\mathrm{36}{p}−\mathrm{27}{p}^{\mathrm{3}} } \\ $$$$\mathrm{4}{x}^{\mathrm{3}} −\mathrm{27}{p}^{\mathrm{2}} {x}^{\mathrm{3}} =\mathrm{4}\:\Leftrightarrow\:{x}^{\mathrm{3}} =\frac{\mathrm{4}}{\mathrm{4}−\mathrm{27}{p}^{\mathrm{2}} } \\ $$$$\Rightarrow \\ $$$$\mathrm{36}{p}−\mathrm{27}{p}^{\mathrm{3}} =\mathrm{8}−\mathrm{54}{p}^{\mathrm{2}} \\ $$$${p}^{\mathrm{3}} −\mathrm{2}{p}^{\mathrm{2}} −\frac{\mathrm{4}}{\mathrm{3}}{p}+\frac{\mathrm{8}}{\mathrm{27}}=\mathrm{0} \\ $$$${p}_{\mathrm{1}} =−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${p}_{\mathrm{2}} =\frac{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$${p}_{\mathrm{3}} =\frac{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\Rightarrow \\ $$$${x}_{\mathrm{1}} =−\frac{\sqrt[{\mathrm{3}}]{\mathrm{4}}}{\mathrm{2}}\wedge{y}_{\mathrm{1}} =\frac{\sqrt[{\mathrm{3}}]{\mathrm{4}}}{\mathrm{3}} \\ $$$${x}_{\mathrm{2}} =\frac{\sqrt[{\mathrm{3}}]{\mathrm{4}}}{\mathrm{4}}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\wedge{y}_{\mathrm{2}} =\frac{\sqrt[{\mathrm{3}}]{\mathrm{4}}}{\mathrm{6}}\left(−\mathrm{1}+\sqrt{\mathrm{3}}\right) \\ $$$${x}_{\mathrm{3}} =−\frac{\sqrt[{\mathrm{3}}]{\mathrm{4}}}{\mathrm{4}}\left(−\mathrm{1}+\sqrt{\mathrm{3}}\right)\wedge{y}_{\mathrm{3}} =−\frac{\sqrt[{\mathrm{3}}]{\mathrm{4}}}{\mathrm{6}}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *