is-this-true-and-is-there-a-proof-k-N-k-gt-1-n-1-k-2-1-k-n-n-1-k-2-1-k-n-1-2-

Question Number 149342 by MJS_new last updated on 04/Aug/21

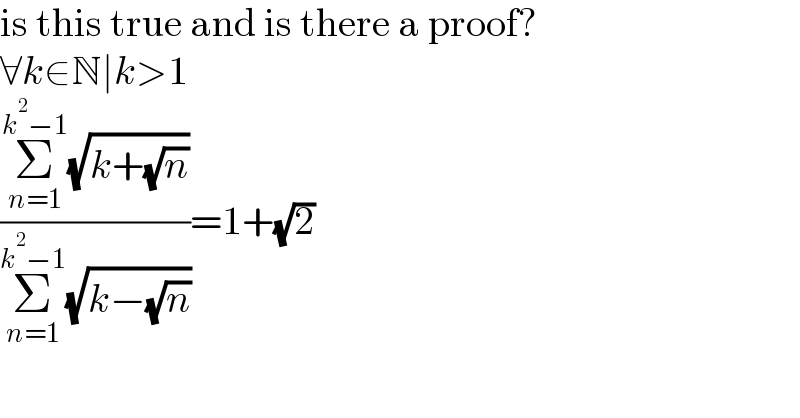
$$\mathrm{is}\:\mathrm{this}\:\mathrm{true}\:\mathrm{and}\:\mathrm{is}\:\mathrm{there}\:\mathrm{a}\:\mathrm{proof}? \\ $$$$\forall{k}\in\mathbb{N}\mid{k}>\mathrm{1} \\ $$$$\frac{\underset{{n}=\mathrm{1}} {\overset{{k}^{\mathrm{2}} −\mathrm{1}} {\sum}}\sqrt{{k}+\sqrt{{n}}}}{\underset{{n}=\mathrm{1}} {\overset{{k}^{\mathrm{2}} −\mathrm{1}} {\sum}}\sqrt{{k}−\sqrt{{n}}}}=\mathrm{1}+\sqrt{\mathrm{2}} \\ $$

Commented by mr W last updated on 04/Aug/21

$${yes},\:{it}'{s}\:{true}. \\ $$

Answered by mr W last updated on 04/Aug/21

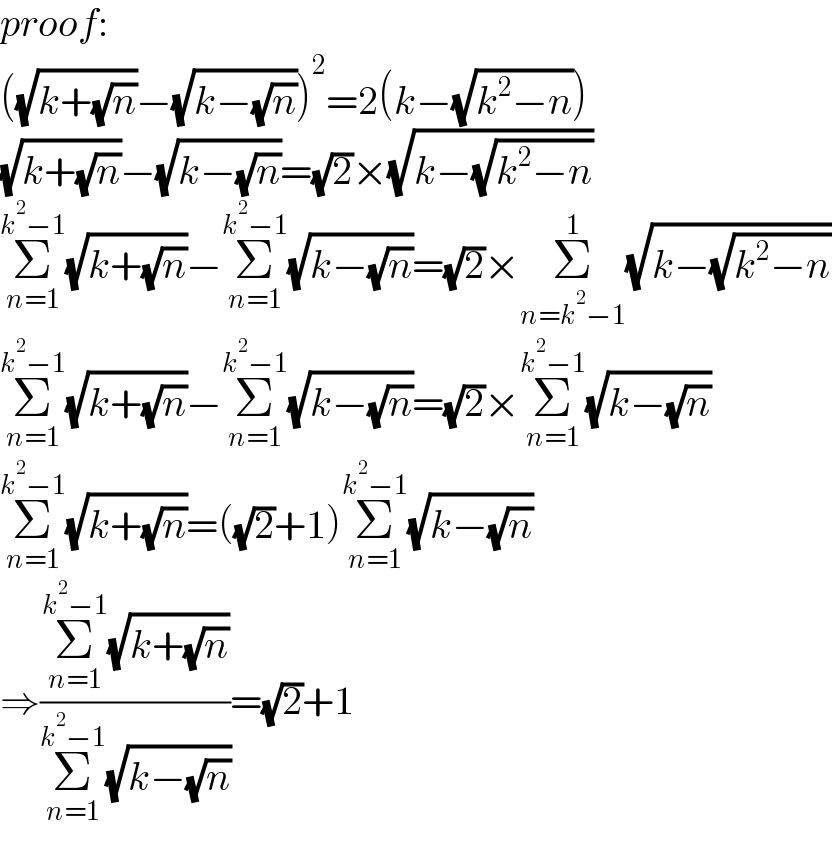
$${proof}: \\ $$$$\left(\sqrt{{k}+\sqrt{{n}}}−\sqrt{{k}−\sqrt{{n}}}\right)^{\mathrm{2}} =\mathrm{2}\left({k}−\sqrt{{k}^{\mathrm{2}} −{n}}\right) \\ $$$$\sqrt{{k}+\sqrt{{n}}}−\sqrt{{k}−\sqrt{{n}}}=\sqrt{\mathrm{2}}×\sqrt{{k}−\sqrt{{k}^{\mathrm{2}} −{n}}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{k}^{\mathrm{2}} −\mathrm{1}} {\sum}}\sqrt{{k}+\sqrt{{n}}}−\underset{{n}=\mathrm{1}} {\overset{{k}^{\mathrm{2}} −\mathrm{1}} {\sum}}\sqrt{{k}−\sqrt{{n}}}=\sqrt{\mathrm{2}}×\underset{{n}={k}^{\mathrm{2}} −\mathrm{1}} {\overset{\mathrm{1}} {\sum}}\sqrt{{k}−\sqrt{{k}^{\mathrm{2}} −{n}}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{k}^{\mathrm{2}} −\mathrm{1}} {\sum}}\sqrt{{k}+\sqrt{{n}}}−\underset{{n}=\mathrm{1}} {\overset{{k}^{\mathrm{2}} −\mathrm{1}} {\sum}}\sqrt{{k}−\sqrt{{n}}}=\sqrt{\mathrm{2}}×\underset{{n}=\mathrm{1}} {\overset{{k}^{\mathrm{2}} −\mathrm{1}} {\sum}}\sqrt{{k}−\sqrt{{n}}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{k}^{\mathrm{2}} −\mathrm{1}} {\sum}}\sqrt{{k}+\sqrt{{n}}}=\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\underset{{n}=\mathrm{1}} {\overset{{k}^{\mathrm{2}} −\mathrm{1}} {\sum}}\sqrt{{k}−\sqrt{{n}}} \\ $$$$\Rightarrow\frac{\underset{{n}=\mathrm{1}} {\overset{{k}^{\mathrm{2}} −\mathrm{1}} {\sum}}\sqrt{{k}+\sqrt{{n}}}}{\underset{{n}=\mathrm{1}} {\overset{{k}^{\mathrm{2}} −\mathrm{1}} {\sum}}\sqrt{{k}−\sqrt{{n}}}}=\sqrt{\mathrm{2}}+\mathrm{1} \\ $$

Commented by MJS_new last updated on 04/Aug/21

$$\mathrm{thank}\:\mathrm{you}! \\ $$

Commented by Tawa11 last updated on 06/Nov/21

$$\mathrm{great} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com