Question Number 175387 by cortano1 last updated on 29/Aug/22
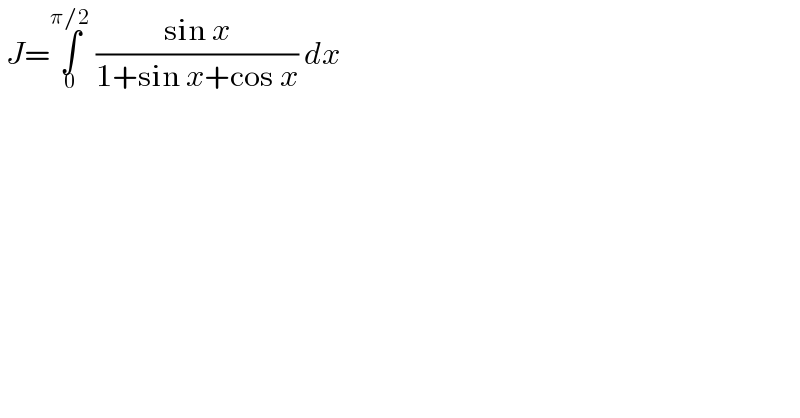
$$\:{J}=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\mathrm{sin}\:{x}}{\mathrm{1}+\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\:{dx} \\ $$
Commented by infinityaction last updated on 29/Aug/22
![J = ∫_0 ^(π/2) ((2sin(x/2)cos (x/2) )/(2sin(x/2) cos(x/2) +2cos^2 (x/2) ))dx J = (1/2)∫_0 ^(π/2 ) (((sin(x/2)+cos(x/2)) −(cos(x/2)− sin(x/2)) )/(sin(x/2) +cos(x/2) ))dx J = (1/2)∫_0 ^(π/2) dx −(1/2)∫_0 ^(π/2) ((cos(x/2)−sin(x/2) )/(sin(x/2)+cos(x/2) ))dx J = (π/4) − [log(sin(x/2) + cos(x/2))]_0 ^(π/2) J = (π/4) − log((√2))](https://www.tinkutara.com/question/Q175391.png)
$$\:\:\:\:{J}\:\:\:=\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{2sin}\frac{{x}}{\mathrm{2}}\mathrm{cos}\:\frac{{x}}{\mathrm{2}}\:}{\mathrm{2sin}\frac{{x}}{\mathrm{2}}\:\mathrm{cos}\frac{{x}}{\mathrm{2}}\:+\mathrm{2cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\:}{dx} \\ $$$$\:{J}\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}\:} \frac{\left(\mathrm{sin}\frac{{x}}{\mathrm{2}}+\mathrm{cos}\frac{{x}}{\mathrm{2}}\right)\:−\left(\mathrm{cos}\frac{{x}}{\mathrm{2}}−\:\mathrm{sin}\frac{{x}}{\mathrm{2}}\right)\:\:}{\mathrm{sin}\frac{{x}}{\mathrm{2}}\:+\mathrm{cos}\frac{{x}}{\mathrm{2}}\:}{dx} \\ $$$$\:\:{J}\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} {dx}\:−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{cos}\frac{{x}}{\mathrm{2}}−\mathrm{sin}\frac{{x}}{\mathrm{2}}\:\:}{\mathrm{sin}\frac{{x}}{\mathrm{2}}+\mathrm{cos}\frac{{x}}{\mathrm{2}}\:\:}{dx}\: \\ $$$$\:\:\:\:{J}\:\:\:\:\:=\:\frac{\pi}{\mathrm{4}}\:−\:\left[\mathrm{log}\left(\mathrm{sin}\frac{{x}}{\mathrm{2}}\:+\:\mathrm{cos}\frac{{x}}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\pi/\mathrm{2}} \\ $$$$\:\:\:\:\:{J}\:\:=\:\:\frac{\pi}{\mathrm{4}}\:−\:\mathrm{log}\left(\sqrt{\mathrm{2}}\right)\:\:\:\:\: \\ $$
Answered by som(math1967) last updated on 29/Aug/22
![2J=∫_0 ^(π/2) dx −∫_0 ^(π/2) (dx/(1+sinx+cosx)) 2J=∫_0 ^(π/2) dx−∫_0 ^(π/2) (dx/(1+2sin(x/2)cos(x/2)+1−2sin^2 (x/2))) 2J= x−∫_0 ^(π/2) ((sec^2 (x/2)dx)/(2sec^2 (x/2)+2tan(x/2)−2tan^2 (x/2))) 2J=x−∫_0 ^(π/2) ((sec^2 (x/2)dx)/(2(1+tan(x/2)))) 2J=[x+ln(1+tan(x/2))]_0 ^(π/2) 2J=(π/2) −ln2 J=(π/4) −ln(√2)](https://www.tinkutara.com/question/Q175389.png)
$$\mathrm{2}{J}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx}\:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{1}+{sinx}+{cosx}} \\ $$$$\mathrm{2}{J}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{1}+\mathrm{2}{sin}\frac{{x}}{\mathrm{2}}{cos}\frac{{x}}{\mathrm{2}}+\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}} \\ $$$$\mathrm{2}{J}=\:{x}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx}}{\mathrm{2}{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\mathrm{2}{tan}\frac{{x}}{\mathrm{2}}−\mathrm{2}{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}} \\ $$$$\mathrm{2}{J}={x}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx}}{\mathrm{2}\left(\mathrm{1}+{tan}\frac{{x}}{\mathrm{2}}\right)} \\ $$$$\mathrm{2}{J}=\left[{x}+{ln}\left(\mathrm{1}+{tan}\frac{{x}}{\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\mathrm{2}{J}=\frac{\pi}{\mathrm{2}}\:−{ln}\mathrm{2} \\ $$$${J}=\frac{\pi}{\mathrm{4}}\:−{ln}\sqrt{\mathrm{2}} \\ $$
Commented by cortano1 last updated on 29/Aug/22

$${yes}\:{sir} \\ $$
Answered by Ramanathan last updated on 29/Aug/22

$$\underset{\mathrm{4}} {\pi} \\ $$$$\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$
