Question Number 108053 by john santu last updated on 14/Aug/20
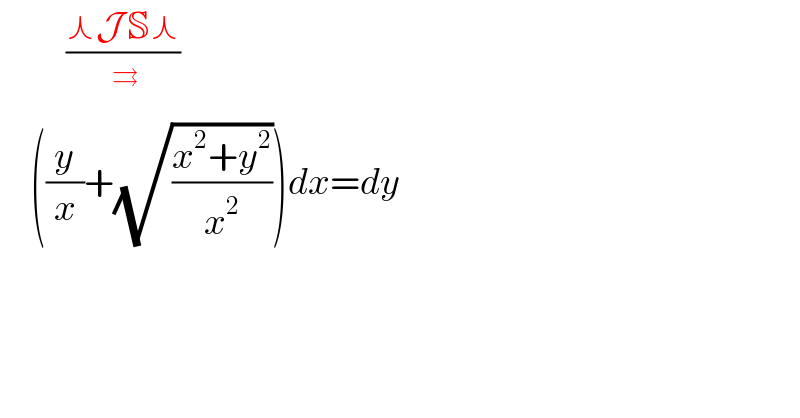
$$\:\:\:\:\:\:\:\:\:\:\:\frac{\curlywedge\mathcal{J}\:\mathbb{S}\curlywedge}{\:^{\rightrightarrows} } \\ $$$$\:\:\:\:\:\left(\frac{{y}}{{x}}+\sqrt{\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }}\right){dx}={dy} \\ $$
Answered by bemath last updated on 14/Aug/20
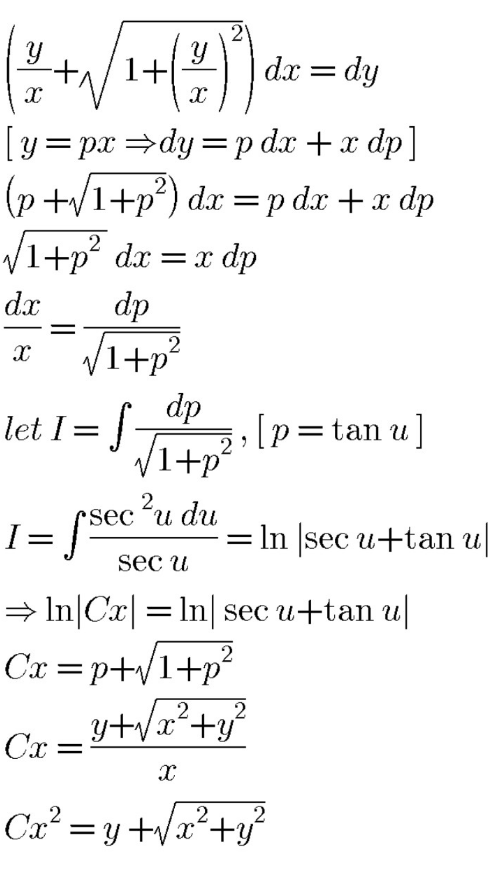
Answered by Dwaipayan Shikari last updated on 14/Aug/20
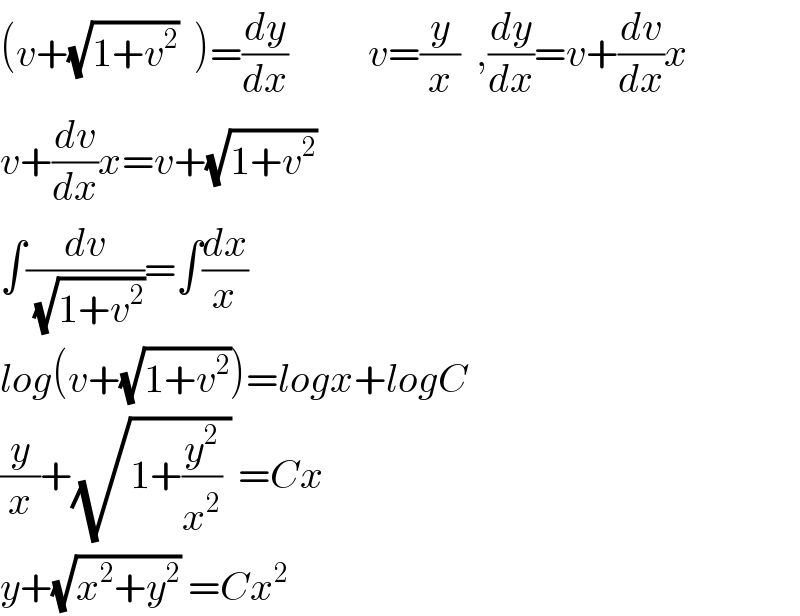
$$\left({v}+\sqrt{\mathrm{1}+{v}^{\mathrm{2}} }\:\:\right)=\frac{{dy}}{{dx}}\:\:\:\:\:\:\:\:\:\:{v}=\frac{{y}}{{x}}\:\:,\frac{{dy}}{{dx}}={v}+\frac{{dv}}{{dx}}{x} \\ $$$${v}+\frac{{dv}}{{dx}}{x}={v}+\sqrt{\mathrm{1}+{v}^{\mathrm{2}} } \\ $$$$\int\frac{{dv}}{\:\sqrt{\mathrm{1}+{v}^{\mathrm{2}} }}=\int\frac{{dx}}{{x}} \\ $$$${log}\left({v}+\sqrt{\mathrm{1}+{v}^{\mathrm{2}} }\right)={logx}+{logC} \\ $$$$\frac{{y}}{{x}}+\sqrt{\mathrm{1}+\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\:}\:={Cx} \\ $$$${y}+\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:={Cx}^{\mathrm{2}} \\ $$
