Menu Close

JS-1-x-1-x-1-x-1-x-1-dx-2-tan-x-1-tan-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 109839 by john santu last updated on 25/Aug/20
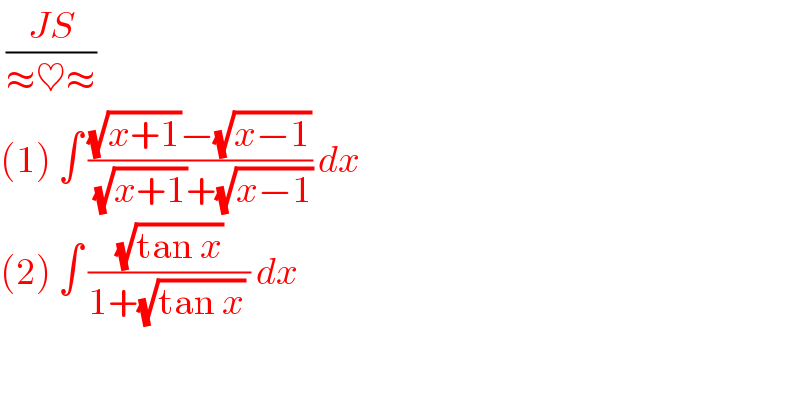
((JS)/(≈♥≈)) (1) ∫ (((√(x+1))−(√(x−1)))/( (√(x+1))+(√(x−1)))) dx (2) ∫ ((√(tan x))/(1+(√(tan x)) )) dx
$$\:\frac{{JS}}{\approx\heartsuit\approx} \\ $$$$\left(\mathrm{1}\right)\:\int\:\frac{\sqrt{{x}+\mathrm{1}}−\sqrt{{x}−\mathrm{1}}}{\:\sqrt{{x}+\mathrm{1}}+\sqrt{{x}−\mathrm{1}}}\:{dx} \\ $$$$\left(\mathrm{2}\right)\:\int\:\frac{\sqrt{\mathrm{tan}\:{x}}}{\mathrm{1}+\sqrt{\mathrm{tan}\:{x}}\:}\:{dx}\: \\ $$
Commented by Her_Majesty last updated on 25/Aug/20
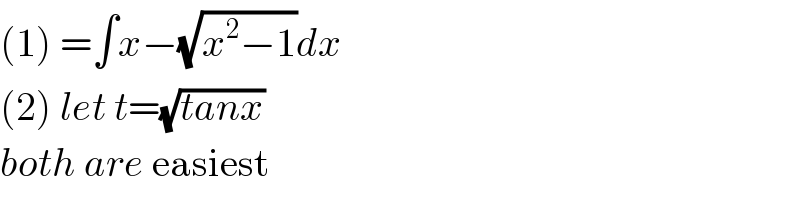
(1) =∫x−(√(x^2 −1))dx (2) let t=(√(tanx)) both are easiest
$$\left(\mathrm{1}\right)\:=\int{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}{dx} \\ $$$$\left(\mathrm{2}\right)\:{let}\:{t}=\sqrt{{tanx}} \\ $$$${both}\:{are}\:\mathrm{easiest} \\ $$
Answered by Dwaipayan Shikari last updated on 25/Aug/20
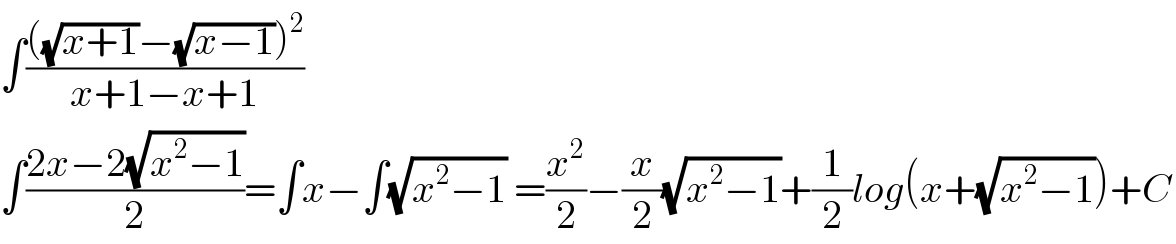
∫((((√(x+1))−(√(x−1)))^2 )/(x+1−x+1)) ∫((2x−2(√(x^2 −1)))/2)=∫x−∫(√(x^2 −1)) =(x^2 /2)−(x/2)(√(x^2 −1))+(1/2)log(x+(√(x^2 −1)))+C
$$\int\frac{\left(\sqrt{{x}+\mathrm{1}}−\sqrt{{x}−\mathrm{1}}\right)^{\mathrm{2}} }{{x}+\mathrm{1}−{x}+\mathrm{1}} \\ $$$$\int\frac{\mathrm{2}{x}−\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}}=\int{x}−\int\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\frac{{x}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}{log}\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)+{C} \\ $$
Answered by bobhans last updated on 26/Aug/20
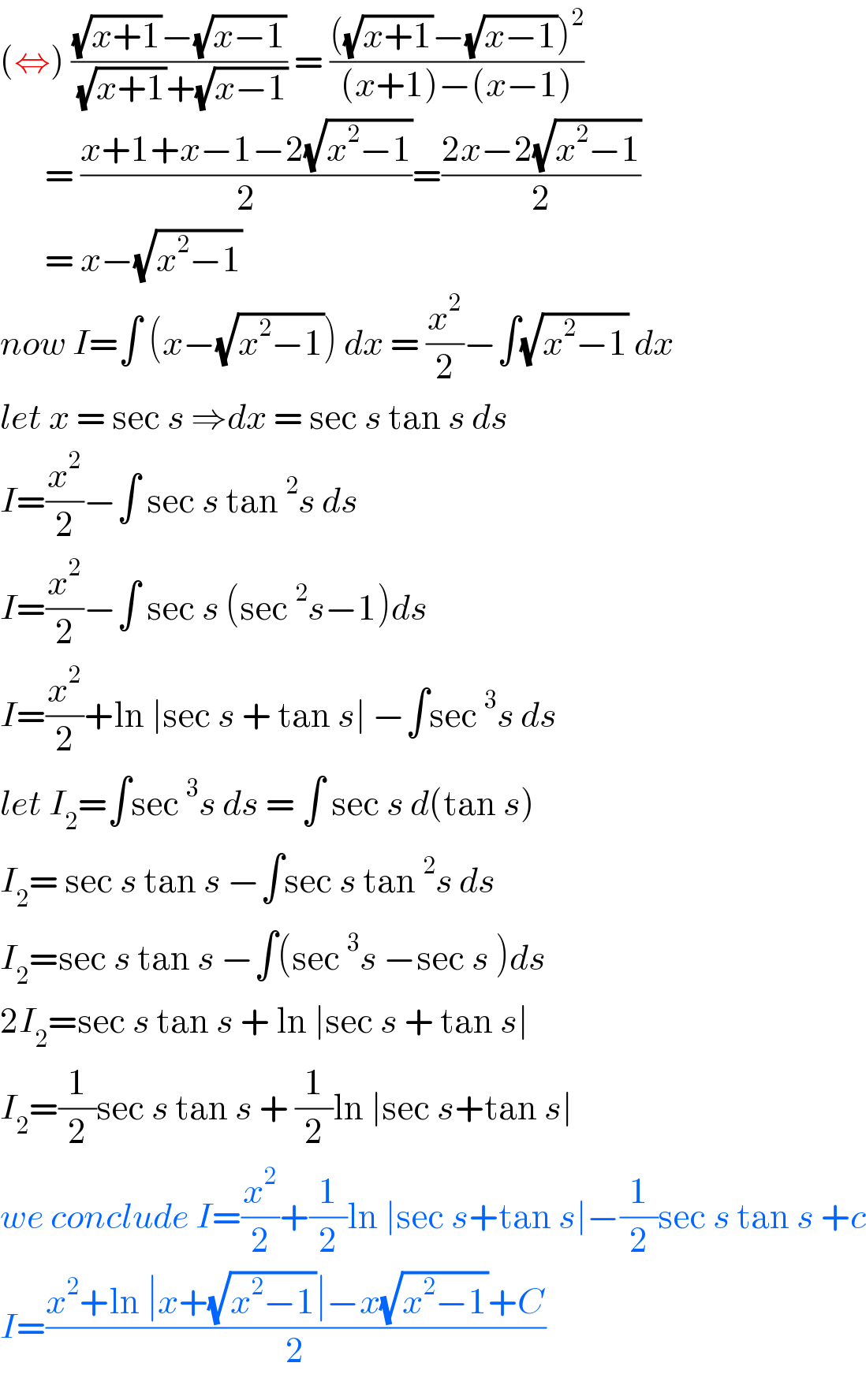
(⇔) (((√(x+1))−(√(x−1)))/( (√(x+1))+(√(x−1)))) = ((((√(x+1))−(√(x−1)))^2 )/((x+1)−(x−1))) = ((x+1+x−1−2(√(x^2 −1)))/2)=((2x−2(√(x^2 −1)))/2) = x−(√(x^2 −1)) now I=∫ (x−(√(x^2 −1))) dx = (x^2 /2)−∫(√(x^2 −1)) dx let x = sec s ⇒dx = sec s tan s ds I=(x^2 /2)−∫ sec s tan^2 s ds I=(x^2 /2)−∫ sec s (sec^2 s−1)ds I=(x^2 /2)+ln ∣sec s + tan s∣ −∫sec^3 s ds let I_2 =∫sec^3 s ds = ∫ sec s d(tan s) I_2 = sec s tan s −∫sec s tan^2 s ds I_2 =sec s tan s −∫(sec^3 s −sec s )ds 2I_2 =sec s tan s + ln ∣sec s + tan s∣ I_2 =(1/2)sec s tan s + (1/2)ln ∣sec s+tan s∣ we conclude I=(x^2 /2)+(1/2)ln ∣sec s+tan s∣−(1/2)sec s tan s +c I=((x^2 +ln ∣x+(√(x^2 −1))∣−x(√(x^2 −1))+C)/2)
$$\left(\Leftrightarrow\right)\:\frac{\sqrt{{x}+\mathrm{1}}−\sqrt{{x}−\mathrm{1}}}{\:\sqrt{{x}+\mathrm{1}}+\sqrt{{x}−\mathrm{1}}}\:=\:\frac{\left(\sqrt{{x}+\mathrm{1}}−\sqrt{{x}−\mathrm{1}}\right)^{\mathrm{2}} }{\left({x}+\mathrm{1}\right)−\left({x}−\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\:=\:\frac{{x}+\mathrm{1}+{x}−\mathrm{1}−\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}}=\frac{\mathrm{2}{x}−\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\:{x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$${now}\:{I}=\int\:\left({x}−\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)\:{dx}\:=\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\int\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:{dx} \\ $$$${let}\:{x}\:=\:\mathrm{sec}\:{s}\:\Rightarrow{dx}\:=\:\mathrm{sec}\:{s}\:\mathrm{tan}\:{s}\:{ds} \\ $$$${I}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\int\:\mathrm{sec}\:{s}\:\mathrm{tan}\:^{\mathrm{2}} {s}\:{ds}\: \\ $$$${I}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\int\:\mathrm{sec}\:{s}\:\left(\mathrm{sec}\:^{\mathrm{2}} {s}−\mathrm{1}\right){ds} \\ $$$${I}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{ln}\:\mid\mathrm{sec}\:{s}\:+\:\mathrm{tan}\:{s}\mid\:−\int\mathrm{sec}\:^{\mathrm{3}} {s}\:{ds} \\ $$$${let}\:{I}_{\mathrm{2}} =\int\mathrm{sec}\:^{\mathrm{3}} {s}\:{ds}\:=\:\int\:\mathrm{sec}\:{s}\:{d}\left(\mathrm{tan}\:{s}\right) \\ $$$${I}_{\mathrm{2}} =\:\mathrm{sec}\:{s}\:\mathrm{tan}\:{s}\:−\int\mathrm{sec}\:{s}\:\mathrm{tan}\:^{\mathrm{2}} {s}\:{ds} \\ $$$${I}_{\mathrm{2}} =\mathrm{sec}\:{s}\:\mathrm{tan}\:{s}\:−\int\left(\mathrm{sec}\:^{\mathrm{3}} {s}\:−\mathrm{sec}\:{s}\:\right){ds} \\ $$$$\mathrm{2}{I}_{\mathrm{2}} =\mathrm{sec}\:{s}\:\mathrm{tan}\:{s}\:+\:\mathrm{ln}\:\mid\mathrm{sec}\:{s}\:+\:\mathrm{tan}\:{s}\mid\: \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:{s}\:\mathrm{tan}\:{s}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{sec}\:{s}+\mathrm{tan}\:{s}\mid \\ $$$${we}\:{conclude}\:{I}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{sec}\:{s}+\mathrm{tan}\:{s}\mid−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:{s}\:\mathrm{tan}\:{s}\:+{c} \\ $$$${I}=\frac{{x}^{\mathrm{2}} +\mathrm{ln}\:\mid{x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\mid−{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}+{C}}{\mathrm{2}} \\ $$
Answered by bobhans last updated on 26/Aug/20
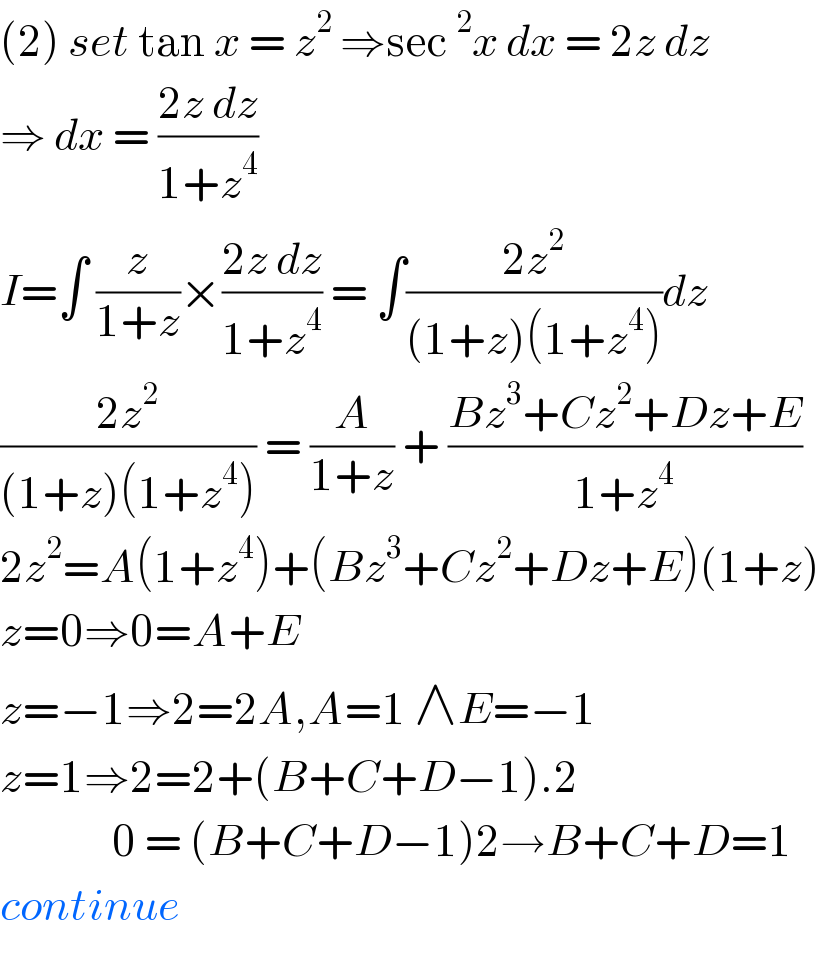
(2) set tan x = z^2 ⇒sec^2 x dx = 2z dz ⇒ dx = ((2z dz)/(1+z^4 )) I=∫ (z/(1+z))×((2z dz)/(1+z^4 )) = ∫((2z^2 )/((1+z)(1+z^4 )))dz ((2z^2 )/((1+z)(1+z^4 ))) = (A/(1+z)) + ((Bz^3 +Cz^2 +Dz+E)/(1+z^4 )) 2z^2 =A(1+z^4 )+(Bz^3 +Cz^2 +Dz+E)(1+z) z=0⇒0=A+E z=−1⇒2=2A,A=1 ∧E=−1 z=1⇒2=2+(B+C+D−1).2 0 = (B+C+D−1)2→B+C+D=1 continue
$$\left(\mathrm{2}\right)\:{set}\:\mathrm{tan}\:{x}\:=\:{z}^{\mathrm{2}} \:\Rightarrow\mathrm{sec}\:^{\mathrm{2}} {x}\:{dx}\:=\:\mathrm{2}{z}\:{dz} \\ $$$$\Rightarrow\:{dx}\:=\:\frac{\mathrm{2}{z}\:{dz}}{\mathrm{1}+{z}^{\mathrm{4}} }\: \\ $$$${I}=\int\:\frac{{z}}{\mathrm{1}+{z}}×\frac{\mathrm{2}{z}\:{dz}}{\mathrm{1}+{z}^{\mathrm{4}} }\:=\:\int\frac{\mathrm{2}{z}^{\mathrm{2}} }{\left(\mathrm{1}+{z}\right)\left(\mathrm{1}+{z}^{\mathrm{4}} \right)}{dz} \\ $$$$\frac{\mathrm{2}{z}^{\mathrm{2}} }{\left(\mathrm{1}+{z}\right)\left(\mathrm{1}+{z}^{\mathrm{4}} \right)}\:=\:\frac{{A}}{\mathrm{1}+{z}}\:+\:\frac{{Bz}^{\mathrm{3}} +{Cz}^{\mathrm{2}} +{Dz}+{E}}{\mathrm{1}+{z}^{\mathrm{4}} } \\ $$$$\mathrm{2}{z}^{\mathrm{2}} ={A}\left(\mathrm{1}+{z}^{\mathrm{4}} \right)+\left({Bz}^{\mathrm{3}} +{Cz}^{\mathrm{2}} +{Dz}+{E}\right)\left(\mathrm{1}+{z}\right) \\ $$$${z}=\mathrm{0}\Rightarrow\mathrm{0}={A}+{E} \\ $$$${z}=−\mathrm{1}\Rightarrow\mathrm{2}=\mathrm{2}{A},{A}=\mathrm{1}\:\wedge{E}=−\mathrm{1} \\ $$$${z}=\mathrm{1}\Rightarrow\mathrm{2}=\mathrm{2}+\left({B}+{C}+{D}−\mathrm{1}\right).\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:=\:\left({B}+{C}+{D}−\mathrm{1}\right)\mathrm{2}\rightarrow{B}+{C}+{D}=\mathrm{1} \\ $$$${continue} \\ $$
Commented by Sarah85 last updated on 26/Aug/20
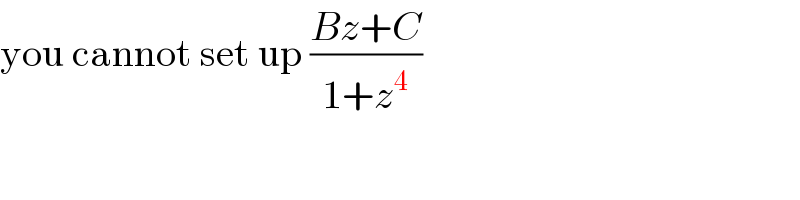
you cannot set up ((Bz+C)/(1+z^4 ))
$$\mathrm{you}\:\mathrm{cannot}\:\mathrm{set}\:\mathrm{up}\:\frac{{Bz}+{C}}{\mathrm{1}+{z}^{\mathrm{4}} }\: \\ $$
Commented by bobhans last updated on 26/Aug/20
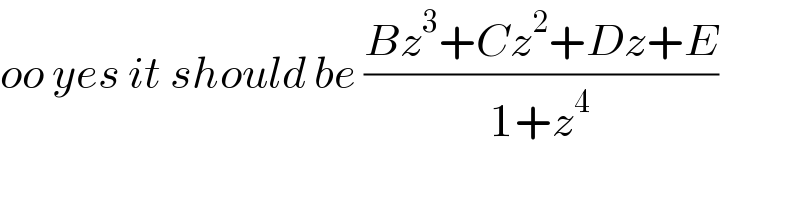
oo yes it should be ((Bz^3 +Cz^2 +Dz+E)/(1+z^4 ))
$${oo}\:{yes}\:{it}\:{should}\:{be}\:\frac{{Bz}^{\mathrm{3}} +{Cz}^{\mathrm{2}} +{Dz}+{E}}{\mathrm{1}+{z}^{\mathrm{4}} } \\ $$
Answered by Sarah85 last updated on 26/Aug/20
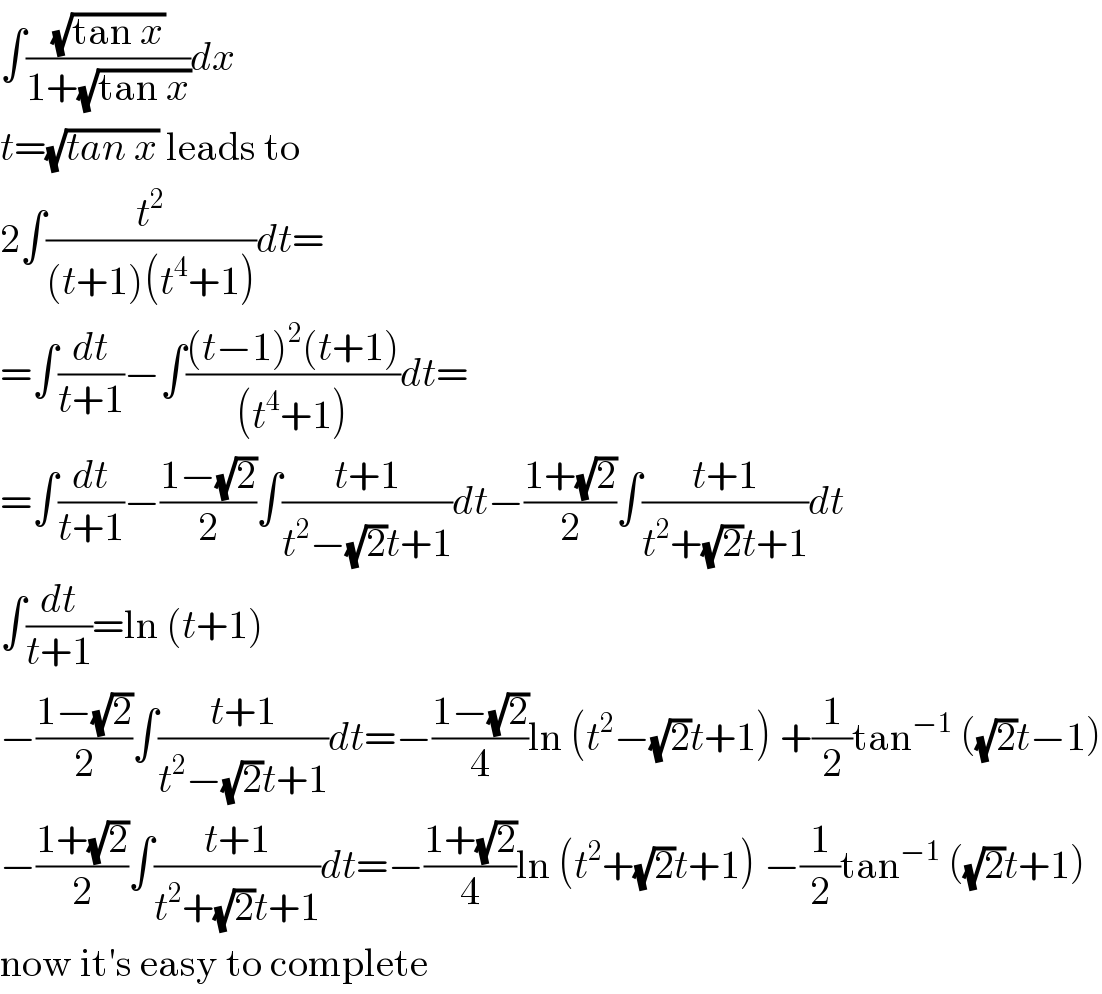
∫((√(tan x))/(1+(√(tan x))))dx t=(√(tan x)) leads to 2∫(t^2 /((t+1)(t^4 +1)))dt= =∫(dt/(t+1))−∫(((t−1)^2 (t+1))/((t^4 +1)))dt= =∫(dt/(t+1))−((1−(√2))/2)∫((t+1)/(t^2 −(√2)t+1))dt−((1+(√2))/2)∫((t+1)/(t^2 +(√2)t+1))dt ∫(dt/(t+1))=ln (t+1) −((1−(√2))/2)∫((t+1)/(t^2 −(√2)t+1))dt=−((1−(√2))/4)ln (t^2 −(√2)t+1) +(1/2)tan^(−1) ((√2)t−1) −((1+(√2))/2)∫((t+1)/(t^2 +(√2)t+1))dt=−((1+(√2))/4)ln (t^2 +(√2)t+1) −(1/2)tan^(−1) ((√2)t+1) now it′s easy to complete
$$\int\frac{\sqrt{\mathrm{tan}\:{x}}}{\mathrm{1}+\sqrt{\mathrm{tan}\:{x}}}{dx} \\ $$$${t}=\sqrt{{tan}\:{x}}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\mathrm{2}\int\frac{{t}^{\mathrm{2}} }{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{4}} +\mathrm{1}\right)}{dt}= \\ $$$$=\int\frac{{dt}}{{t}+\mathrm{1}}−\int\frac{\left({t}−\mathrm{1}\right)^{\mathrm{2}} \left({t}+\mathrm{1}\right)}{\left({t}^{\mathrm{4}} +\mathrm{1}\right)}{dt}= \\ $$$$=\int\frac{{dt}}{{t}+\mathrm{1}}−\frac{\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}{dt}−\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}}{dt} \\ $$$$\int\frac{{dt}}{{t}+\mathrm{1}}=\mathrm{ln}\:\left({t}+\mathrm{1}\right) \\ $$$$−\frac{\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}{dt}=−\frac{\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{ln}\:\left({t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \:\left(\sqrt{\mathrm{2}}{t}−\mathrm{1}\right) \\ $$$$−\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}}\int\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}}{dt}=−\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}+\mathrm{1}\right)\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}^{−\mathrm{1}} \:\left(\sqrt{\mathrm{2}}{t}+\mathrm{1}\right) \\ $$$$\mathrm{now}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{complete} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *