Question Number 107871 by john santu last updated on 13/Aug/20
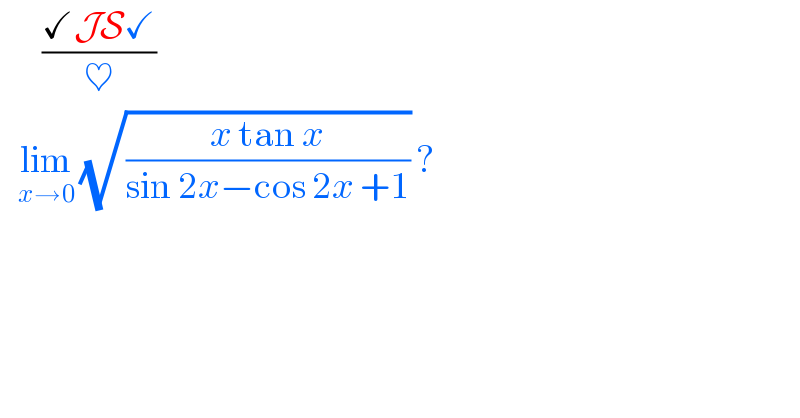
$$\:\:\:\:\:\:\:\frac{\checkmark\mathcal{JS}\checkmark}{\heartsuit} \\ $$$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt{\frac{{x}\:\mathrm{tan}\:{x}}{\mathrm{sin}\:\mathrm{2}{x}−\mathrm{cos}\:\mathrm{2}{x}\:+\mathrm{1}}}\:?\: \\ $$
Commented by bemath last updated on 13/Aug/20
Answered by hgrocks last updated on 13/Aug/20

$$ \\ $$$$\mathrm{L}^{\mathrm{2}} \:=\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}\:} \frac{\mathrm{x}\:\mathrm{tanx}}{\mathrm{2sinx}.\mathrm{cosx}\:+\:\mathrm{2sin}^{\mathrm{2}} \mathrm{x}} \\ $$$$\:\:\:\:\:=\:\left(\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \frac{\mathrm{xtanx}}{\mathrm{2sinx}}\:\right).\:\left(\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}\:} \frac{\mathrm{1}}{\mathrm{cosx}\:+\:\mathrm{sinx}}\right) \\ $$$$\:\:\:\:\:=\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\frac{\mathrm{x}}{\mathrm{2}}.\frac{\mathrm{tanx}}{\mathrm{x}}.\frac{\mathrm{x}}{\mathrm{sinx}} \\ $$$$\left(\mathrm{Note}\::\:\mathrm{The}\:\mathrm{Function}\:\mathrm{Is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{as}\:\mathrm{x}\rightarrow\mathrm{0}^{−} \right) \\ $$$$\mathrm{So}\:\mathrm{Only}\:\mathrm{R}.\mathrm{H}.\mathrm{L}\:\mathrm{exists} \\ $$$$\mathrm{L}\:=\:\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \sqrt{\mathrm{L}^{\mathrm{2}} }\:=\:\mathrm{0} \\ $$$$\bigstar\mathfrak{hg}\bigstar\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by bemath last updated on 13/Aug/20
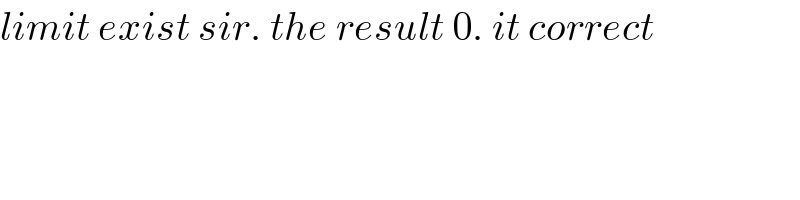
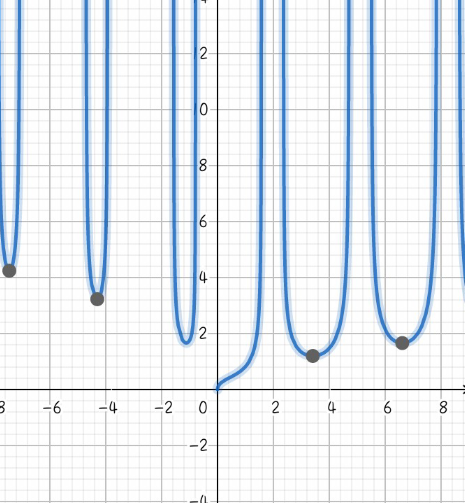
$${limit}\:{exist}\:{sir}.\:{the}\:{result}\:\mathrm{0}.\:{it}\:{correct} \\ $$
