Question Number 171071 by mathocean1 last updated on 07/Jun/22
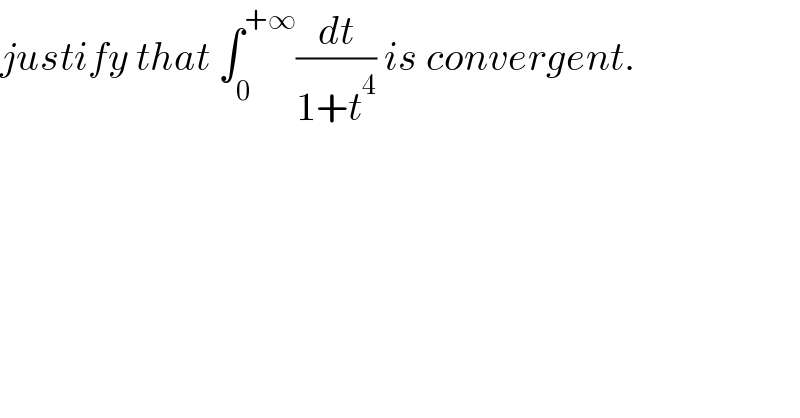
$${justify}\:{that}\:\int_{\mathrm{0}} ^{+\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:{is}\:{convergent}. \\ $$
Answered by aleks041103 last updated on 07/Jun/22
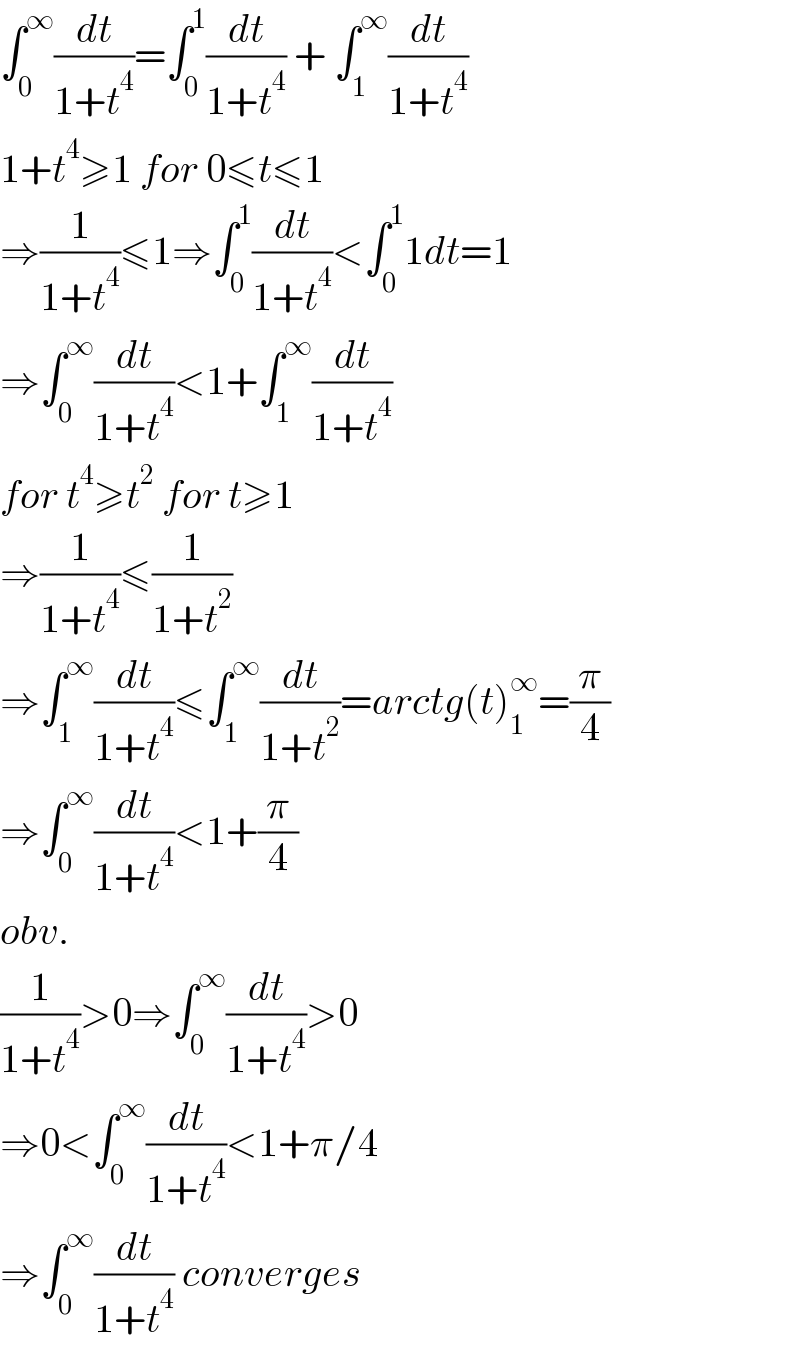
$$\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:+\:\int_{\mathrm{1}} ^{\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} } \\ $$$$\mathrm{1}+{t}^{\mathrm{4}} \geqslant\mathrm{1}\:{for}\:\mathrm{0}\leqslant{t}\leqslant\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{4}} }\leqslant\mathrm{1}\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }<\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{1}{dt}=\mathrm{1} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }<\mathrm{1}+\int_{\mathrm{1}} ^{\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} } \\ $$$${for}\:{t}^{\mathrm{4}} \geqslant{t}^{\mathrm{2}} \:{for}\:{t}\geqslant\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{4}} }\leqslant\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\Rightarrow\int_{\mathrm{1}} ^{\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\leqslant\int_{\mathrm{1}} ^{\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }={arctg}\left({t}\right)_{\mathrm{1}} ^{\infty} =\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }<\mathrm{1}+\frac{\pi}{\mathrm{4}} \\ $$$${obv}. \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{4}} }>\mathrm{0}\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }>\mathrm{0} \\ $$$$\Rightarrow\mathrm{0}<\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }<\mathrm{1}+\pi/\mathrm{4} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:{converges} \\ $$
