Question Number 186187 by aba last updated on 02/Feb/23
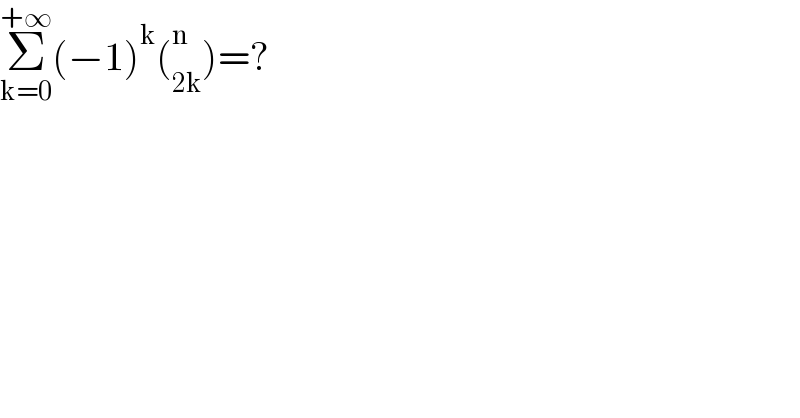
$$\underset{\mathrm{k}=\mathrm{0}} {\overset{+\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{k}} \left(_{\mathrm{2k}} ^{\mathrm{n}} \right)=? \\ $$
Commented by mr W last updated on 02/Feb/23

$${for}\:{k}=\mathrm{0}\:…\:+\infty \\ $$$$\begin{pmatrix}{{n}}\\{\mathrm{2}{k}}\end{pmatrix}\:{is}\:{non}−{sense},\:{no}\:{matter}\:{what} \\ $$$${value}\:{n}\:{has}.\:{so}\:{please}\:{tell}\:{what}\:{you}\: \\ $$$${mean}\:{with}\:\begin{pmatrix}{{n}}\\{\mathrm{2}{k}}\end{pmatrix}. \\ $$
Commented by aba last updated on 02/Feb/23

$$ \\ $$$$\underset{\mathrm{k}=\mathrm{0}} {\overset{+\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{k}} \mathrm{C}_{\mathrm{n}} ^{\mathrm{2k}} =? \\ $$
Commented by mr W last updated on 02/Feb/23

$${as}\:{i}\:{said}\:{for}\:{k}=\mathrm{0}\:{to}\:+\infty,\:\left(_{{n}} ^{\mathrm{2}{k}} \right)\:{or}\:{C}_{{n}} ^{\mathrm{2}{k}} \:{is} \\ $$$${not}\:{defined}\:{except}\:{n}=\mathrm{0}.\:{but}\:{then}\:{the} \\ $$$${question}\:{is}\:\underset{{k}=\mathrm{0}} {\overset{+\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} =?,\:{which}\:{is}\:{also} \\ $$$${non}−{sense}.\:{therefore}\:{the}\:{question}\:{is} \\ $$$${non}−{sense}.\:{if}\:{you}\:{have}\:{copied}\:{the} \\ $$$${question}\:{from}\:{somewhere},\:{check} \\ $$$${again}\:{if}\:{you}\:{have}\:{copied}\:{correctely}. \\ $$$${if}\:{you}\:{have}\:{created}\:{the}\:{question}\:{by} \\ $$$${yourself},\:{then}\:{it}'{s}\:{a}\:{bad}\:{attempt}. \\ $$
Commented by aba last updated on 02/Feb/23

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
