Question Number 150374 by mathdanisur last updated on 11/Aug/21
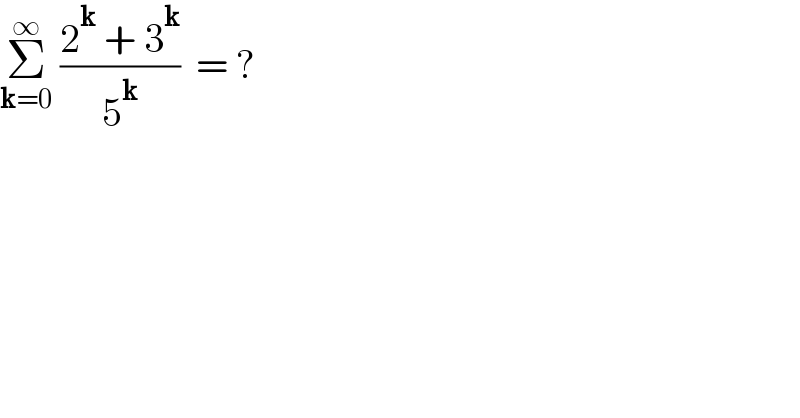
$$\underset{\boldsymbol{\mathrm{k}}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{2}^{\boldsymbol{\mathrm{k}}} \:+\:\mathrm{3}^{\boldsymbol{\mathrm{k}}} }{\mathrm{5}^{\boldsymbol{\mathrm{k}}} }\:\:=\:? \\ $$
Answered by eman_64 last updated on 11/Aug/21
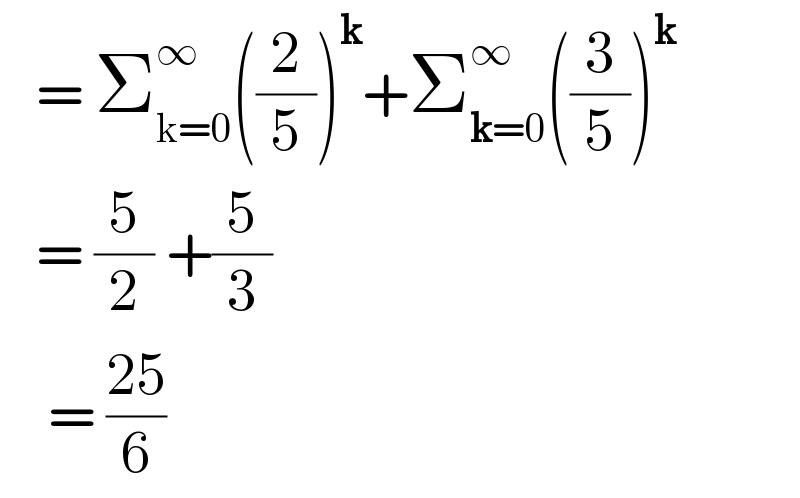
$$\:\:\:=\:\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \left(\frac{\mathrm{2}}{\mathrm{5}}\right)^{\boldsymbol{\mathrm{k}}} +\sum_{\boldsymbol{\mathrm{k}}=\mathrm{0}} ^{\infty} \left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{\boldsymbol{\mathrm{k}}} \:\: \\ $$$$\:\:\:=\:\frac{\mathrm{5}}{\mathrm{2}}\:+\frac{\mathrm{5}}{\mathrm{3}}\:\:\: \\ $$$$\:\:\:\:=\:\frac{\mathrm{25}}{\mathrm{6}} \\ $$
Commented by mathdanisur last updated on 11/Aug/21

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Ser} \\ $$
