Question Number 154824 by talminator2856791 last updated on 21/Sep/21
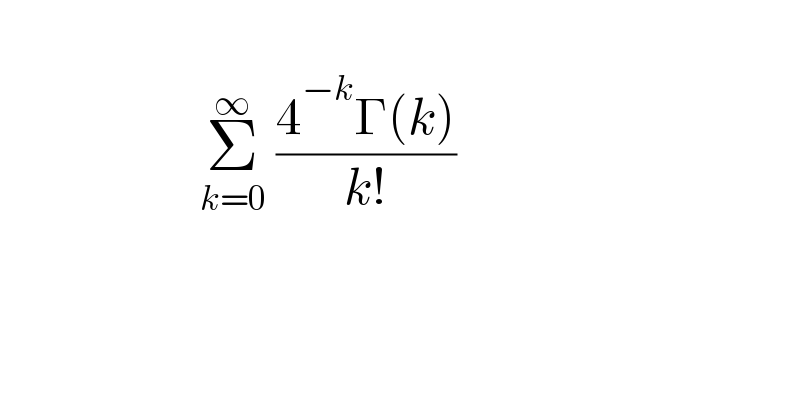
$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{4}^{−{k}} \Gamma\left({k}\right)}{{k}!} \\ $$$$\: \\ $$
Answered by Ar Brandon last updated on 21/Sep/21
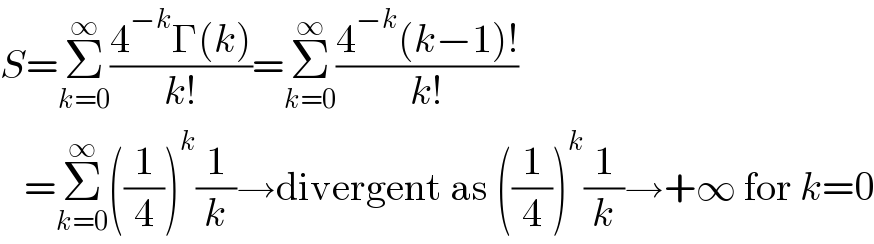
$${S}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{4}^{−{k}} \Gamma\left({k}\right)}{{k}!}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{4}^{−{k}} \left({k}−\mathrm{1}\right)!}{{k}!} \\ $$$$\:\:\:=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{k}} \frac{\mathrm{1}}{{k}}\rightarrow\mathrm{divergent}\:\mathrm{as}\:\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{k}} \frac{\mathrm{1}}{{k}}\rightarrow+\infty\:\mathrm{for}\:{k}=\mathrm{0} \\ $$
Commented by talminator2856791 last updated on 22/Sep/21

$$\:\mathrm{wrong}. \\ $$
