Question Number 144825 by mathdanisur last updated on 29/Jun/21
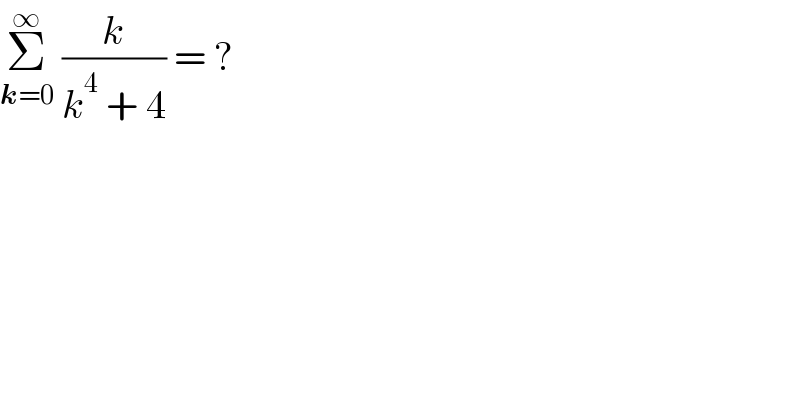
$$\underset{\boldsymbol{{k}}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{k}}{{k}^{\mathrm{4}} \:+\:\mathrm{4}}\:=\:? \\ $$
Answered by Dwaipayan Shikari last updated on 29/Jun/21

$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}}{{k}^{\mathrm{4}} +\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({k}^{\mathrm{2}} −\mathrm{2}{k}+\mathrm{2}\right)}−\frac{\mathrm{1}}{\left({k}^{\mathrm{2}} +\mathrm{2}{k}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{5}}−…\right)=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by mathdanisur last updated on 29/Jun/21

$${thank}\:{you}\:{Sir},\:{but}\:\underset{\boldsymbol{{k}}=\mathrm{0}} {\overset{\infty} {\sum}} \\ $$
Commented by Dwaipayan Shikari last updated on 29/Jun/21
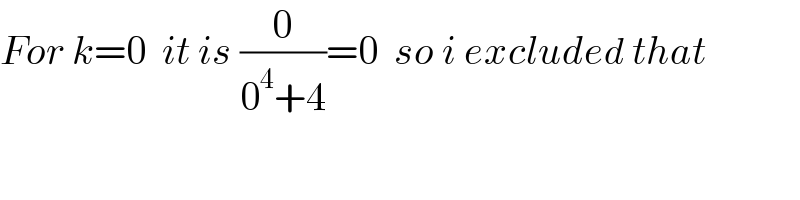
$${For}\:{k}=\mathrm{0}\:\:{it}\:{is}\:\frac{\mathrm{0}}{\mathrm{0}^{\mathrm{4}} +\mathrm{4}}=\mathrm{0}\:\:{so}\:{i}\:{excluded}\:{that} \\ $$
Commented by mathdanisur last updated on 29/Jun/21

$${Thankyou}\:{Sir} \\ $$
