Question Number 103410 by Ar Brandon last updated on 14/Jul/20
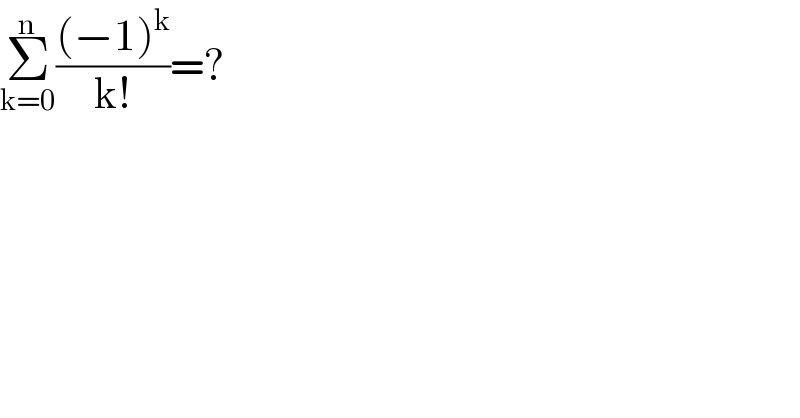
$$\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}!}=? \\ $$
Answered by mathmax by abdo last updated on 15/Jul/20
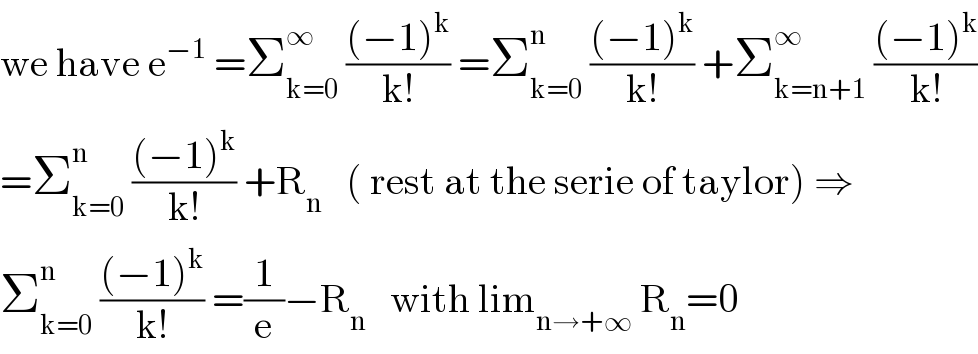
$$\mathrm{we}\:\mathrm{have}\:\mathrm{e}^{−\mathrm{1}} \:=\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}!}\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}!}\:+\sum_{\mathrm{k}=\mathrm{n}+\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}!} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}!}\:+\mathrm{R}_{\mathrm{n}} \:\:\:\left(\:\mathrm{rest}\:\mathrm{at}\:\mathrm{the}\:\mathrm{serie}\:\mathrm{of}\:\mathrm{taylor}\right)\:\Rightarrow \\ $$$$\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}!}\:=\frac{\mathrm{1}}{\mathrm{e}}−\mathrm{R}_{\mathrm{n}} \:\:\:\mathrm{with}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{R}_{\mathrm{n}} =\mathrm{0} \\ $$
