Menu Close

k-1-1-k-1-sin-k-k-

Tinku Tara 0 Comments
Pin




Question Number 116965 by Dwaipayan Shikari last updated on 08/Oct/20
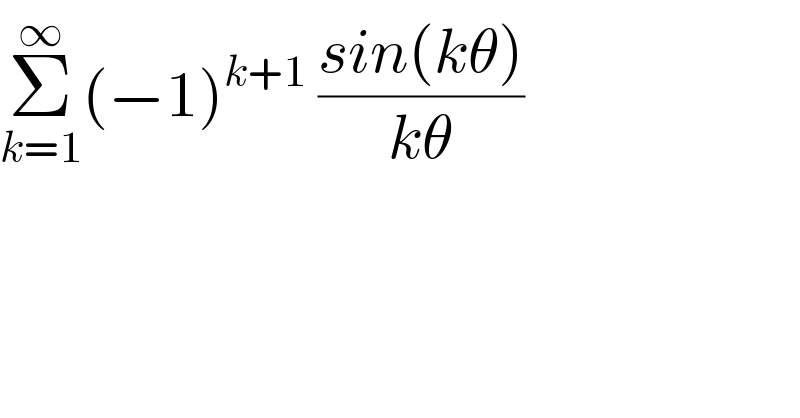
Σ_(k=1) ^∞ (−1)^(k+1) ((sin(kθ))/(kθ))
$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} \:\frac{{sin}\left({k}\theta\right)}{{k}\theta} \\ $$
Answered by Bird last updated on 08/Oct/20
let g(u) =Σ_(k=1) ^∞ (−1)^(k+1 ) ((sin(kx))/(kx))u^k with ∣u∣<1 ⇒g^′ (u) =(1/x)Σ_(k=1) ^∞ (−1)^(k+1) sin(kx)u^(k−1) =(1/x)Σ_(k=0) ^∞ (−1)^k sin((k+1)x)u^k =(1/x)Im(Σ_(k=0) ^∞ (−1)^k e^(i)k+1)x) u^k ) but Σ_(k=0) ^∞ (−1)^k e^(ix) e^(ikx) u^k =e^(ix) Σ_(k=0) ^∞ (−1)^k (u e^(ix) )^k =e^(ix) ×(1/(1+ue^(ix) )) =((cosx +isinx)/(1+ucosx +iu sinx)) =(((cosx+isinx)(1+ucosx−iu sinx))/((1+ucosx)^2 +u^2 sin^2 x)) =((cosx(1+ucosx)−iucosxsinx+isinx(1+ucosx)+usin^2 x)/(1+2ucosx +u^2 )) ⇒Im(Σ...) =((sinx)/(u^2 +2u cosx +1)) ⇒g^′ (u) =((sinx)/(x(u^(2 ) +2u cosx +1))) ⇒g(u) =((sinx)/x)∫ (du/(u^(2 ) +2u cosx +1)) but ∫ (du/(u^(2 ) +2u cosx+1)) =∫ (du/(u^2 +2u cosx +cos^2 x +sin^2 x)) =∫ (du/((u+cosx)^2 +sin^2 x)) =_(u+cosx =sinx z) ∫ ((sinx dz)/(sin^2 x(1+z^2 ))) =(1/(sinx)) arctan(((u+cosx)/(sinx))) +C ⇒ g(u)=(1/x)arctan(((u+cosx)/(sinx))) +C u=1 ⇒S(x) =(1/x)arctan(((1+cosx)/(sinx)))+C =(1/x)arctan(((2cos^2 ((x/2)))/(2cos((x/2))sin((x/2)))))+C =(1/x)arctsn((1/(tan((x/2))))) +C =(1/x)((π/2) −(x/2)) +C =(π/(2x))−(1/2) +C x=π ⇒S(π)=0 =C ⇒ S(x) =((π−x)/(2x))
$${let}\:{g}\left({u}\right)\:=\sum_{{k}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{{k}+\mathrm{1}\:} \frac{{sin}\left({kx}\right)}{{kx}}{u}^{{k}} \:{with}\:\mid{u}\mid<\mathrm{1} \\ $$$$\Rightarrow{g}^{'} \left({u}\right)\:=\frac{\mathrm{1}}{{x}}\sum_{{k}=\mathrm{1}} ^{\infty} \left(−\mathrm{1}\right)^{{k}+\mathrm{1}} {sin}\left({kx}\right){u}^{{k}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{{x}}\sum_{{k}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{k}} {sin}\left(\left({k}+\mathrm{1}\right){x}\right){u}^{{k}} \\ $$$$=\frac{\mathrm{1}}{{x}}{Im}\left(\sum_{{k}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{k}} \:{e}^{\left.{i}\left.\right){k}+\mathrm{1}\right){x}} \:{u}^{{k}} \right) \\ $$$${but}\:\sum_{{k}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{k}} \:{e}^{{ix}} \:{e}^{{ikx}} \:{u}^{{k}} \\ $$$$={e}^{{ix}} \:\sum_{{k}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{k}} \left({u}\:{e}^{{ix}} \right)^{{k}} \\ $$$$={e}^{{ix}} ×\frac{\mathrm{1}}{\mathrm{1}+{ue}^{{ix}} } \\ $$$$=\frac{{cosx}\:+{isinx}}{\mathrm{1}+{ucosx}\:+{iu}\:{sinx}} \\ $$$$=\frac{\left({cosx}+{isinx}\right)\left(\mathrm{1}+{ucosx}−{iu}\:{sinx}\right)}{\left(\mathrm{1}+{ucosx}\right)^{\mathrm{2}} \:+{u}^{\mathrm{2}} \:{sin}^{\mathrm{2}} {x}} \\ $$$$=\frac{{cosx}\left(\mathrm{1}+{ucosx}\right)−{iucosxsinx}+{isinx}\left(\mathrm{1}+{ucosx}\right)+{usin}^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{2}{ucosx}\:+{u}^{\mathrm{2}} } \\ $$$$\Rightarrow{Im}\left(\Sigma…\right)\:=\frac{{sinx}}{{u}^{\mathrm{2}} \:+\mathrm{2}{u}\:{cosx}\:+\mathrm{1}} \\ $$$$\Rightarrow{g}^{'} \left({u}\right)\:=\frac{{sinx}}{{x}\left({u}^{\mathrm{2}\:} \:+\mathrm{2}{u}\:{cosx}\:+\mathrm{1}\right)} \\ $$$$\Rightarrow{g}\left({u}\right)\:=\frac{{sinx}}{{x}}\int\:\:\frac{{du}}{{u}^{\mathrm{2}\:} +\mathrm{2}{u}\:{cosx}\:+\mathrm{1}} \\ $$$${but}\:\int\:\:\frac{{du}}{{u}^{\mathrm{2}\:} +\mathrm{2}{u}\:{cosx}+\mathrm{1}} \\ $$$$=\int\:\:\frac{{du}}{{u}^{\mathrm{2}} \:+\mathrm{2}{u}\:{cosx}\:+{cos}^{\mathrm{2}} {x}\:+{sin}^{\mathrm{2}} {x}} \\ $$$$=\int\:\:\frac{{du}}{\left({u}+{cosx}\right)^{\mathrm{2}} \:+{sin}^{\mathrm{2}} {x}} \\ $$$$=_{{u}+{cosx}\:={sinx}\:{z}} \:\:\:\int\:\:\frac{{sinx}\:{dz}}{{sin}^{\mathrm{2}} {x}\left(\mathrm{1}+{z}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{{sinx}}\:{arctan}\left(\frac{{u}+{cosx}}{{sinx}}\right)\:+{C}\:\Rightarrow \\ $$$${g}\left({u}\right)=\frac{\mathrm{1}}{{x}}{arctan}\left(\frac{{u}+{cosx}}{{sinx}}\right)\:+{C} \\ $$$${u}=\mathrm{1}\:\Rightarrow{S}\left({x}\right)\:=\frac{\mathrm{1}}{{x}}{arctan}\left(\frac{\mathrm{1}+{cosx}}{{sinx}}\right)+{C} \\ $$$$=\frac{\mathrm{1}}{{x}}{arctan}\left(\frac{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{cos}\left(\frac{{x}}{\mathrm{2}}\right){sin}\left(\frac{{x}}{\mathrm{2}}\right)}\right)+{C} \\ $$$$=\frac{\mathrm{1}}{{x}}{arctsn}\left(\frac{\mathrm{1}}{{tan}\left(\frac{{x}}{\mathrm{2}}\right)}\right)\:+{C} \\ $$$$=\frac{\mathrm{1}}{{x}}\left(\frac{\pi}{\mathrm{2}}\:−\frac{{x}}{\mathrm{2}}\right)\:+{C} \\ $$$$=\frac{\pi}{\mathrm{2}{x}}−\frac{\mathrm{1}}{\mathrm{2}}\:+{C} \\ $$$${x}=\pi\:\Rightarrow{S}\left(\pi\right)=\mathrm{0}\:={C}\:\Rightarrow \\ $$$${S}\left({x}\right)\:=\frac{\pi−{x}}{\mathrm{2}{x}} \\ $$
Commented by Dwaipayan Shikari last updated on 08/Oct/20
Thanking you
$${Thanking}\:{you} \\ $$
Commented by Bird last updated on 08/Oct/20
you are welcome
$${you}\:{are}\:{welcome} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *