Question Number 144947 by mathdanisur last updated on 30/Jun/21
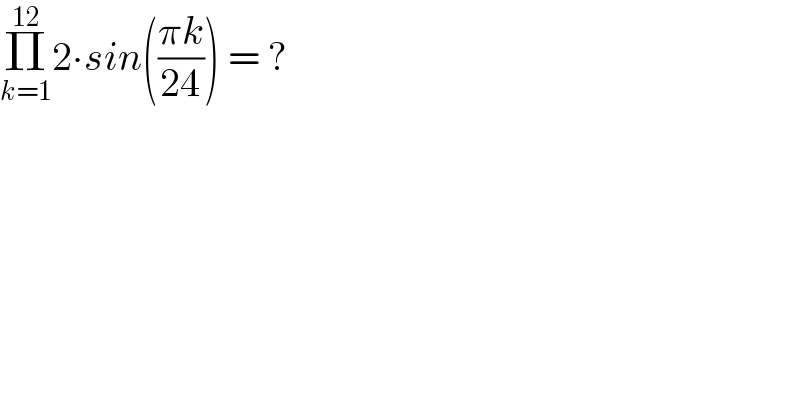
$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{12}} {\prod}}\mathrm{2}\centerdot{sin}\left(\frac{\pi{k}}{\mathrm{24}}\right)\:=\:? \\ $$
Answered by Olaf_Thorendsen last updated on 01/Jul/21
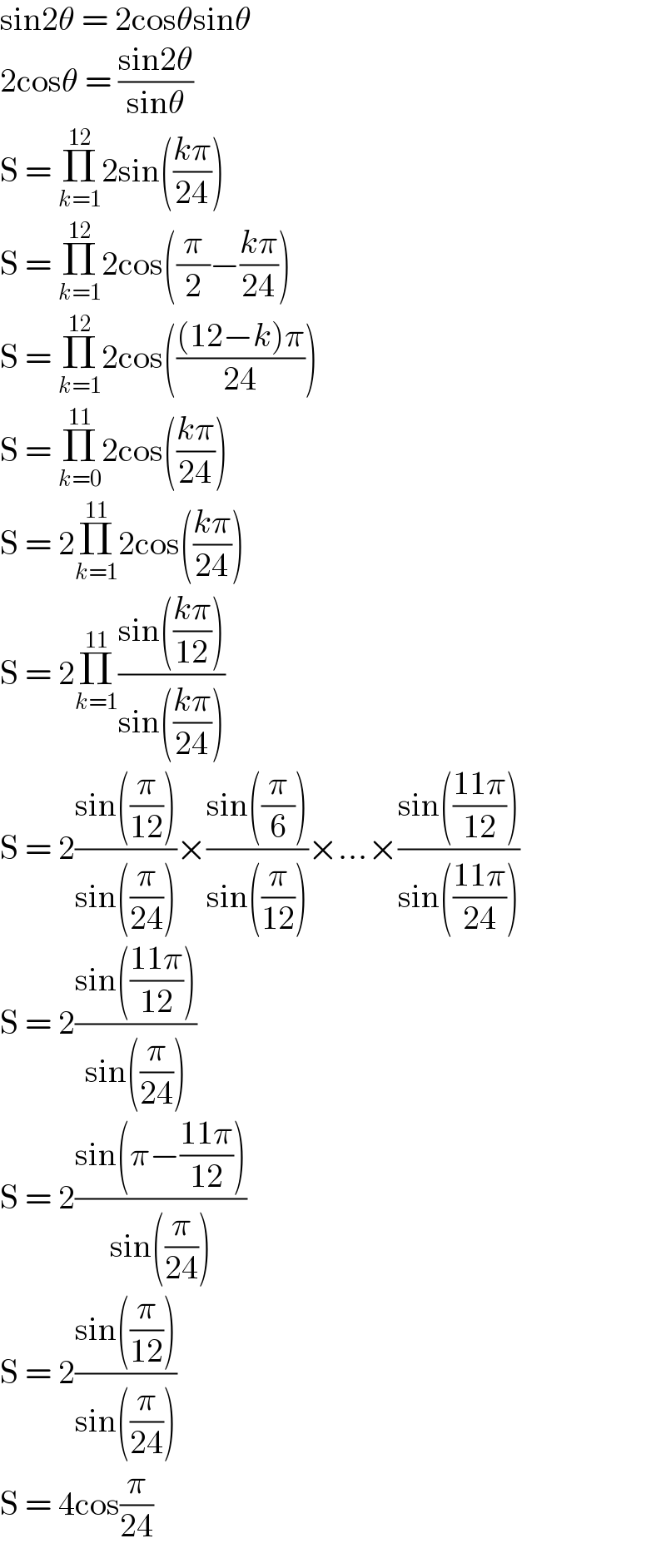
$$\mathrm{sin2}\theta\:=\:\mathrm{2cos}\theta\mathrm{sin}\theta \\ $$$$\mathrm{2cos}\theta\:=\:\frac{\mathrm{sin2}\theta}{\mathrm{sin}\theta} \\ $$$$\mathrm{S}\:=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{12}} {\prod}}\mathrm{2sin}\left(\frac{{k}\pi}{\mathrm{24}}\right) \\ $$$$\mathrm{S}\:=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{12}} {\prod}}\mathrm{2cos}\left(\frac{\pi}{\mathrm{2}}−\frac{{k}\pi}{\mathrm{24}}\right) \\ $$$$\mathrm{S}\:=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{12}} {\prod}}\mathrm{2cos}\left(\frac{\left(\mathrm{12}−{k}\right)\pi}{\mathrm{24}}\right) \\ $$$$\mathrm{S}\:=\:\underset{{k}=\mathrm{0}} {\overset{\mathrm{11}} {\prod}}\mathrm{2cos}\left(\frac{{k}\pi}{\mathrm{24}}\right) \\ $$$$\mathrm{S}\:=\:\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{\mathrm{11}} {\prod}}\mathrm{2cos}\left(\frac{{k}\pi}{\mathrm{24}}\right) \\ $$$$\mathrm{S}\:=\:\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{\mathrm{11}} {\prod}}\frac{\mathrm{sin}\left(\frac{{k}\pi}{\mathrm{12}}\right)}{\mathrm{sin}\left(\frac{{k}\pi}{\mathrm{24}}\right)} \\ $$$$\mathrm{S}\:=\:\mathrm{2}\frac{\mathrm{sin}\left(\frac{\pi}{\mathrm{12}}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{24}}\right)}×\frac{\mathrm{sin}\left(\frac{\pi}{\mathrm{6}}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{12}}\right)}×…×\frac{\mathrm{sin}\left(\frac{\mathrm{11}\pi}{\mathrm{12}}\right)}{\mathrm{sin}\left(\frac{\mathrm{11}\pi}{\mathrm{24}}\right)} \\ $$$$\mathrm{S}\:=\:\mathrm{2}\frac{\mathrm{sin}\left(\frac{\mathrm{11}\pi}{\mathrm{12}}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{24}}\right)} \\ $$$$\mathrm{S}\:=\:\mathrm{2}\frac{\mathrm{sin}\left(\pi−\frac{\mathrm{11}\pi}{\mathrm{12}}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{24}}\right)} \\ $$$$\mathrm{S}\:=\:\mathrm{2}\frac{\mathrm{sin}\left(\frac{\pi}{\mathrm{12}}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{24}}\right)} \\ $$$$\mathrm{S}\:=\:\mathrm{4cos}\frac{\pi}{\mathrm{24}} \\ $$
Commented by mathdanisur last updated on 01/Jul/21
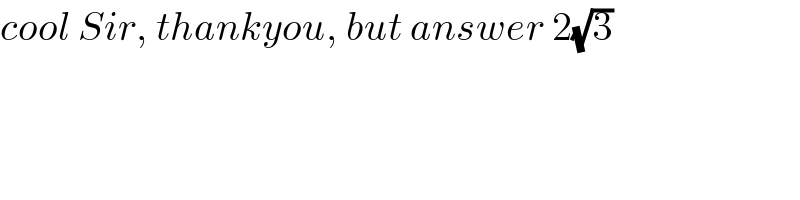
$${cool}\:{Sir},\:{thankyou},\:{but}\:{answer}\:\mathrm{2}\sqrt{\mathrm{3}} \\ $$
Commented by Ar Brandon last updated on 01/Jul/21
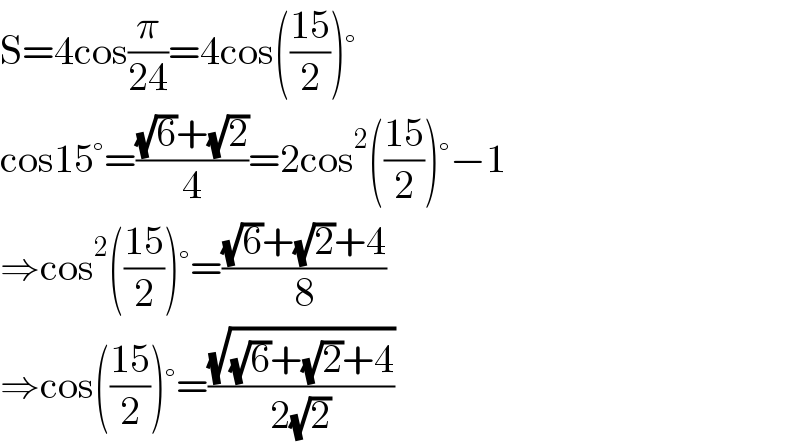
$$\mathrm{S}=\mathrm{4cos}\frac{\pi}{\mathrm{24}}=\mathrm{4cos}\left(\frac{\mathrm{15}}{\mathrm{2}}\right)° \\ $$$$\mathrm{cos15}°=\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{4}}=\mathrm{2cos}^{\mathrm{2}} \left(\frac{\mathrm{15}}{\mathrm{2}}\right)°−\mathrm{1} \\ $$$$\Rightarrow\mathrm{cos}^{\mathrm{2}} \left(\frac{\mathrm{15}}{\mathrm{2}}\right)°=\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}+\mathrm{4}}{\mathrm{8}} \\ $$$$\Rightarrow\mathrm{cos}\left(\frac{\mathrm{15}}{\mathrm{2}}\right)°=\frac{\sqrt{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}+\mathrm{4}}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$
