Question Number 144981 by mathdanisur last updated on 01/Jul/21
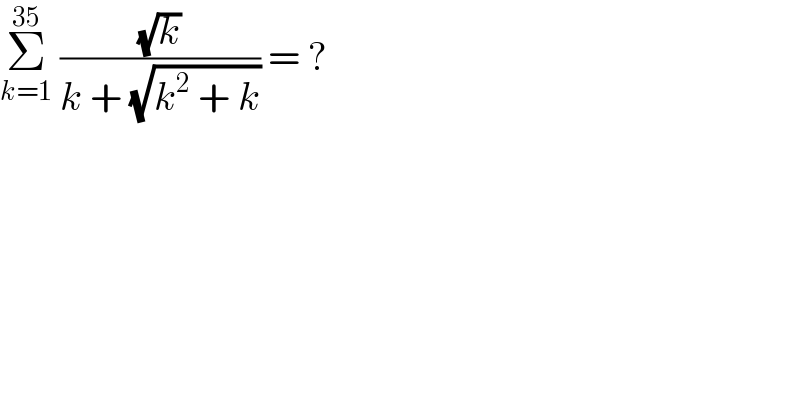
$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{35}} {\sum}}\:\frac{\sqrt{{k}}}{{k}\:+\:\sqrt{{k}^{\mathrm{2}} \:+\:{k}}}\:=\:? \\ $$
Answered by liberty last updated on 01/Jul/21

$$\:\frac{\sqrt{\mathrm{k}}}{\mathrm{k}+\sqrt{\mathrm{k}^{\mathrm{2}} +\mathrm{k}}}\:=\:\frac{\sqrt{\mathrm{k}}\:\left(\mathrm{k}−\sqrt{\mathrm{k}^{\mathrm{2}} +\mathrm{k}}\right)}{−\mathrm{k}} \\ $$$$=\:−\sqrt{\mathrm{k}}\:+\frac{\sqrt{\mathrm{k}^{\mathrm{2}} +\mathrm{k}}}{\:\sqrt{\mathrm{k}}}\: \\ $$$$=−\sqrt{\mathrm{k}}+\sqrt{\mathrm{k}+\mathrm{1}} \\ $$$$=\sqrt{\mathrm{k}+\mathrm{1}}−\sqrt{\mathrm{k}} \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{35}} {\sum}}\left(\sqrt{\mathrm{k}+\mathrm{1}}−\sqrt{\mathrm{k}}\right)=\underset{\mathrm{telescopic}\:\mathrm{series}} {\underbrace{\:\mathrm{6}−\mathrm{1}\:=\:\mathrm{5}}} \\ $$
Commented by mathdanisur last updated on 01/Jul/21
$${thank}\:{you}\:{Sir},\:{cool} \\ $$
