Question Number 103673 by bobhans last updated on 16/Jul/20
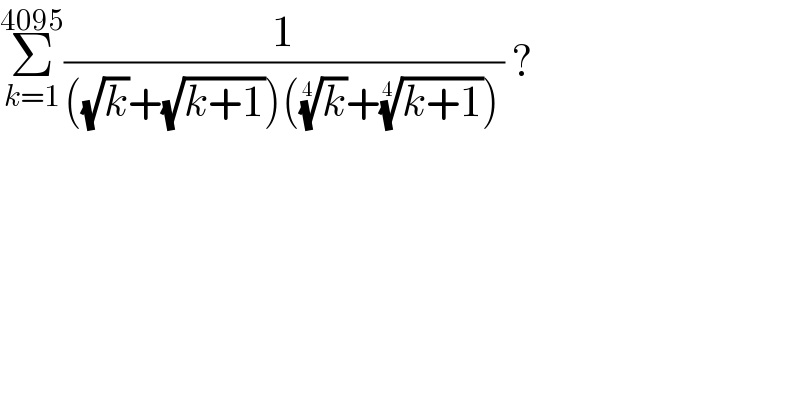
$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{4095}} {\sum}}\frac{\mathrm{1}}{\left(\sqrt{{k}}+\sqrt{{k}+\mathrm{1}}\right)\left(\sqrt[{\mathrm{4}}]{{k}}+\sqrt[{\mathrm{4}}]{{k}+\mathrm{1}}\right)}\:? \\ $$
Answered by bramlex last updated on 16/Jul/20

$$\frac{\mathrm{1}}{\left(\sqrt{\mathrm{k}}+\sqrt{\mathrm{k}+\mathrm{1}}\right)\left(\sqrt[{\mathrm{4}}]{\mathrm{k}}+\sqrt[{\mathrm{4}}]{\mathrm{k}+\mathrm{1}}\right)}\:×\frac{\sqrt[{\mathrm{4}}]{\mathrm{k}+\mathrm{1}}−\sqrt[{\mathrm{4}}]{\mathrm{k}}}{\:\sqrt[{\mathrm{4}}]{\mathrm{k}+\mathrm{1}}−\sqrt[{\mathrm{4}}]{\mathrm{k}}}= \\ $$$$\frac{\sqrt[{\mathrm{4}}]{\mathrm{k}+\mathrm{1}}−\sqrt[{\mathrm{4}}]{\mathrm{k}}}{\left(\sqrt{\mathrm{k}+\mathrm{1}}+\sqrt{\mathrm{k}}\right)\left(\sqrt{\mathrm{k}+\mathrm{1}}−\sqrt{\mathrm{k}}\right)}\:=\:\sqrt[{\mathrm{4}}]{\mathrm{k}+\mathrm{1}}−\sqrt[{\mathrm{4}}]{\mathrm{k}} \\ $$$$\mathrm{now}\:\mathrm{S}=\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{4095}} {\sum}}\left(\sqrt[{\mathrm{4}}]{\mathrm{k}+\mathrm{1}}−\sqrt[{\mathrm{4}}]{\mathrm{k}}\right)\:=\sqrt[{\mathrm{4}}]{\mathrm{4096}}−\mathrm{1}=\mathrm{7} \\ $$$$\left(\mathrm{note}\:\mathrm{telecoping}\:\mathrm{series}\right) \\ $$
