k-1-49-1-k-k-2-1-

Question Number 121246 by benjo_mathlover last updated on 06/Nov/20

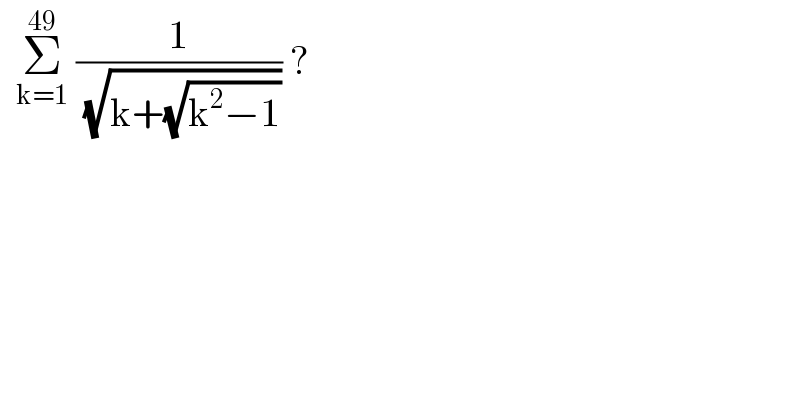
Σ_(k=1) ^(49) (1/( (√(k+(√(k^2 −1)))))) ?

$$\:\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{49}} {\sum}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{k}+\sqrt{\mathrm{k}^{\mathrm{2}} −\mathrm{1}}}}\:? \\ $$

Answered by liberty last updated on 06/Nov/20

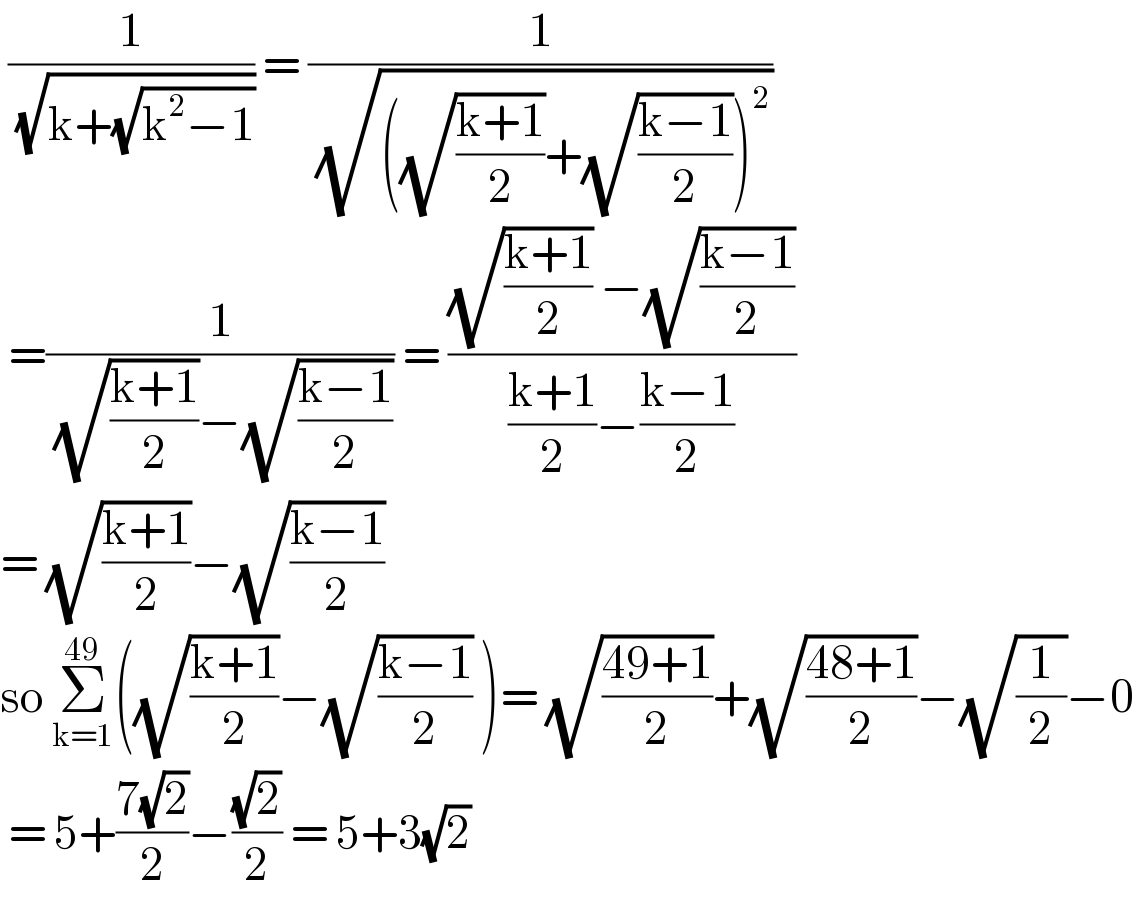
(1/( (√(k+(√(k^2 −1)))))) = (1/( (√(((√((k+1)/2))+(√((k−1)/2)))^2 )))) =(1/( (√((k+1)/2))−(√((k−1)/2)))) = (((√((k+1)/2)) −(√((k−1)/2)))/(((k+1)/2)−((k−1)/2))) = (√((k+1)/2))−(√((k−1)/2)) so Σ_(k=1) ^(49) ((√((k+1)/2))−(√((k−1)/2)) )= (√((49+1)/2))+(√((48+1)/2))−(√(1/2))−0 = 5+((7(√2))/2)−((√2)/2) = 5+3(√2)

$$\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{k}+\sqrt{\mathrm{k}^{\mathrm{2}} −\mathrm{1}}}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\left(\sqrt{\frac{\mathrm{k}+\mathrm{1}}{\mathrm{2}}}+\sqrt{\frac{\mathrm{k}−\mathrm{1}}{\mathrm{2}}}\right)^{\mathrm{2}} }} \\ $$$$\:=\frac{\mathrm{1}}{\:\sqrt{\frac{\mathrm{k}+\mathrm{1}}{\mathrm{2}}}−\sqrt{\frac{\mathrm{k}−\mathrm{1}}{\mathrm{2}}}}\:=\:\frac{\sqrt{\frac{\mathrm{k}+\mathrm{1}}{\mathrm{2}}}\:−\sqrt{\frac{\mathrm{k}−\mathrm{1}}{\mathrm{2}}}}{\frac{\mathrm{k}+\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{k}−\mathrm{1}}{\mathrm{2}}} \\ $$$$=\:\sqrt{\frac{\mathrm{k}+\mathrm{1}}{\mathrm{2}}}−\sqrt{\frac{\mathrm{k}−\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{so}\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{49}} {\sum}}\left(\sqrt{\frac{\mathrm{k}+\mathrm{1}}{\mathrm{2}}}−\sqrt{\frac{\mathrm{k}−\mathrm{1}}{\mathrm{2}}}\:\right)=\:\sqrt{\frac{\mathrm{49}+\mathrm{1}}{\mathrm{2}}}+\sqrt{\frac{\mathrm{48}+\mathrm{1}}{\mathrm{2}}}−\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}−\mathrm{0} \\ $$$$\:=\:\mathrm{5}+\frac{\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:=\:\mathrm{5}+\mathrm{3}\sqrt{\mathrm{2}}\: \\ $$

Answered by Dwaipayan Shikari last updated on 06/Nov/20

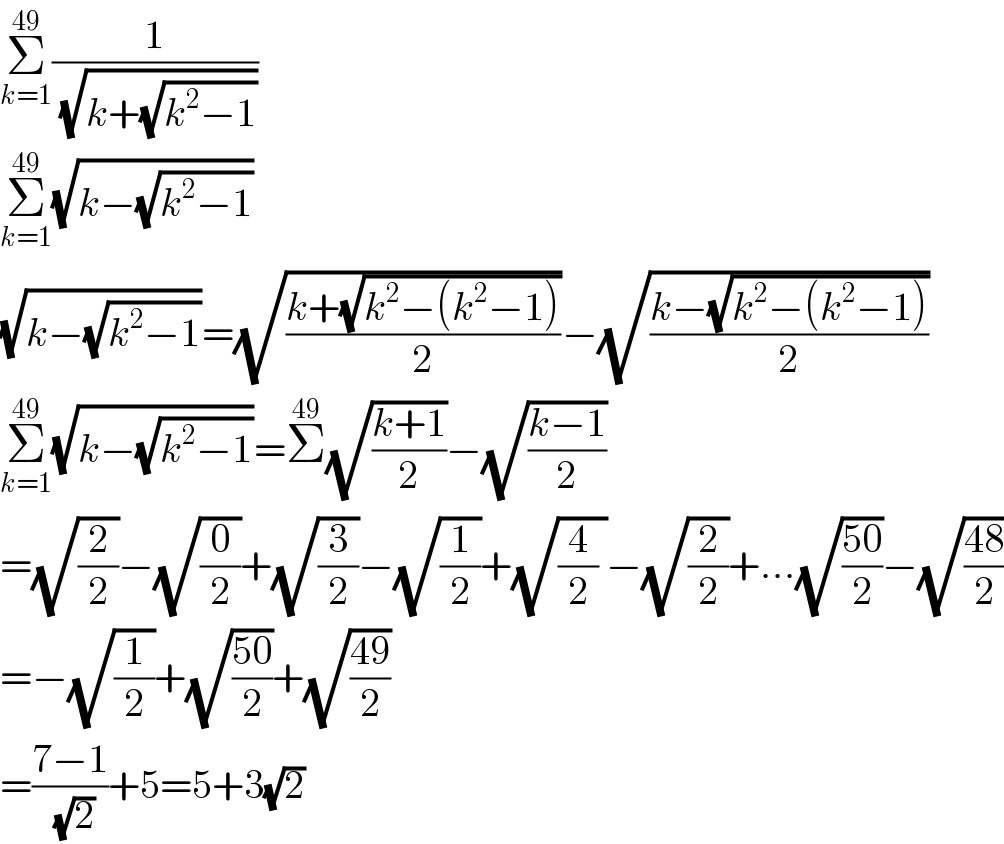
Σ_(k=1) ^(49) (1/( (√(k+(√(k^2 −1)))))) Σ_(k=1) ^(49) (√(k−(√(k^2 −1)))) (√(k−(√(k^2 −1))))=(√((k+(√(k^2 −(k^2 −1))))/2))−(√((k−(√(k^2 −(k^2 −1))))/2)) Σ_(k=1) ^(49) (√(k−(√(k^2 −1))))=Σ^(49) (√((k+1)/2))−(√((k−1)/2)) =(√(2/2))−(√(0/2))+(√(3/2))−(√(1/2))+(√((4/2) ))−(√(2/2))+...(√((50)/2))−(√((48)/2)) =−(√(1/2))+(√((50)/2))+(√((49)/2)) =((7−1)/( (√2)))+5=5+3(√2)

$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{49}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{k}+\sqrt{{k}^{\mathrm{2}} −\mathrm{1}}}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{49}} {\sum}}\sqrt{{k}−\sqrt{{k}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\sqrt{{k}−\sqrt{{k}^{\mathrm{2}} −\mathrm{1}}}=\sqrt{\frac{{k}+\sqrt{{k}^{\mathrm{2}} −\left({k}^{\mathrm{2}} −\mathrm{1}\right)}}{\mathrm{2}}}−\sqrt{\frac{{k}−\sqrt{{k}^{\mathrm{2}} −\left({k}^{\mathrm{2}} −\mathrm{1}\right)}}{\mathrm{2}}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{49}} {\sum}}\sqrt{{k}−\sqrt{{k}^{\mathrm{2}} −\mathrm{1}}}=\overset{\mathrm{49}} {\sum}\sqrt{\frac{{k}+\mathrm{1}}{\mathrm{2}}}−\sqrt{\frac{{k}−\mathrm{1}}{\mathrm{2}}} \\ $$$$=\sqrt{\frac{\mathrm{2}}{\mathrm{2}}}−\sqrt{\frac{\mathrm{0}}{\mathrm{2}}}+\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}−\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}+\sqrt{\frac{\mathrm{4}}{\mathrm{2}}\:}−\sqrt{\frac{\mathrm{2}}{\mathrm{2}}}+…\sqrt{\frac{\mathrm{50}}{\mathrm{2}}}−\sqrt{\frac{\mathrm{48}}{\mathrm{2}}} \\ $$$$=−\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}+\sqrt{\frac{\mathrm{50}}{\mathrm{2}}}+\sqrt{\frac{\mathrm{49}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{7}−\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\mathrm{5}=\mathrm{5}+\mathrm{3}\sqrt{\mathrm{2}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply