Question Number 37859 by kunal1234523 last updated on 18/Jun/18
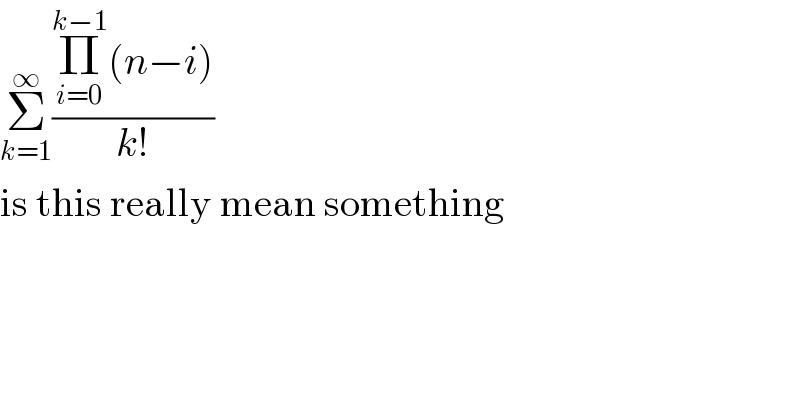
$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\underset{{i}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\prod}}\left({n}−{i}\right)}{{k}!} \\ $$$$\mathrm{is}\:\mathrm{this}\:\mathrm{really}\:\mathrm{mean}\:\mathrm{something} \\ $$
Commented by math khazana by abdo last updated on 18/Jun/18
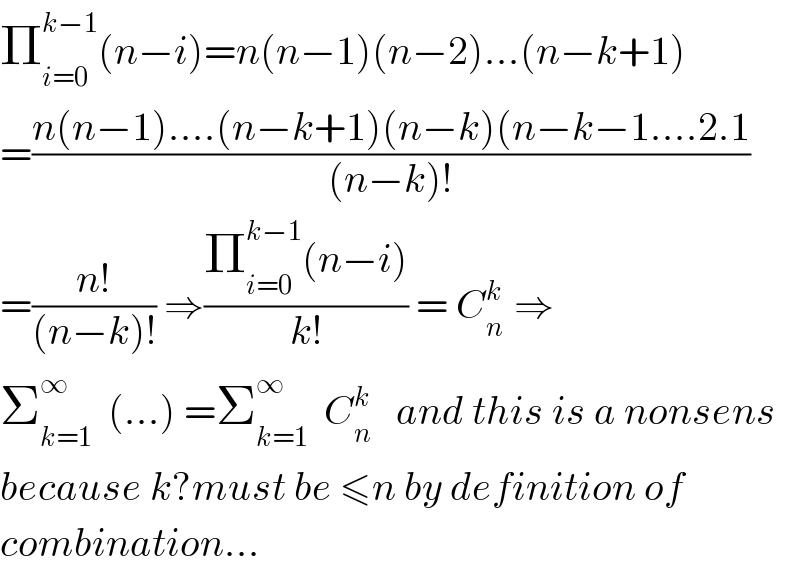
$$\prod_{{i}=\mathrm{0}} ^{{k}−\mathrm{1}} \left({n}−{i}\right)={n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)…\left({n}−{k}+\mathrm{1}\right) \\ $$$$=\frac{{n}\left({n}−\mathrm{1}\right)….\left({n}−{k}+\mathrm{1}\right)\left({n}−{k}\right)\left({n}−{k}−\mathrm{1}….\mathrm{2}.\mathrm{1}\right.}{\left({n}−{k}\right)!} \\ $$$$=\frac{{n}!}{\left({n}−{k}\right)!}\:\Rightarrow\frac{\prod_{{i}=\mathrm{0}} ^{{k}−\mathrm{1}} \left({n}−{i}\right)}{{k}!}\:=\:{C}_{{n}} ^{{k}\:} \:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{\infty} \:\:\left(…\right)\:=\sum_{{k}=\mathrm{1}} ^{\infty} \:\:{C}_{{n}} ^{{k}} \:\:\:{and}\:{this}\:{is}\:{a}\:{nonsens}\:\:\: \\ $$$${because}\:{k}?{must}\:{be}\:\leqslant{n}\:{by}\:{definition}\:{of}\: \\ $$$${combination}… \\ $$
