Question Number 185293 by SANOGO last updated on 19/Jan/23
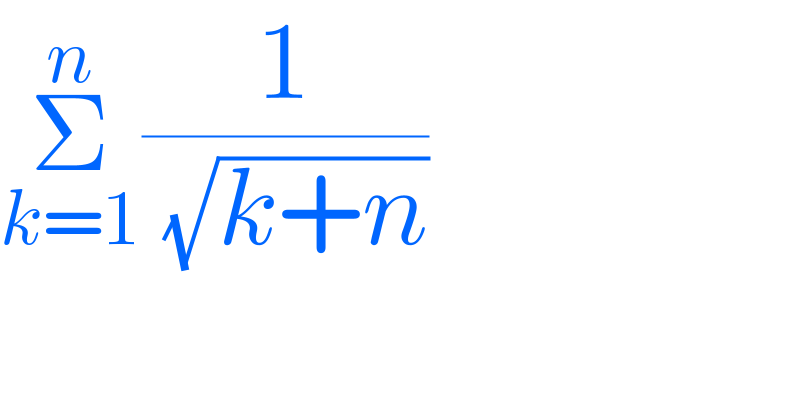
$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{k}+{n}}} \\ $$
Commented by aleks041103 last updated on 20/Jan/23
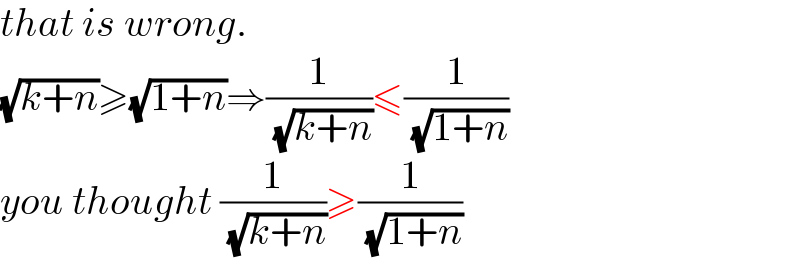
$${that}\:{is}\:{wrong}. \\ $$$$\sqrt{{k}+{n}}\geqslant\sqrt{\mathrm{1}+{n}}\Rightarrow\frac{\mathrm{1}}{\:\sqrt{{k}+{n}}}\leqslant\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{n}}} \\ $$$${you}\:{thought}\:\frac{\mathrm{1}}{\:\sqrt{{k}+{n}}}\geqslant\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{n}}}\: \\ $$
Commented by Frix last updated on 20/Jan/23
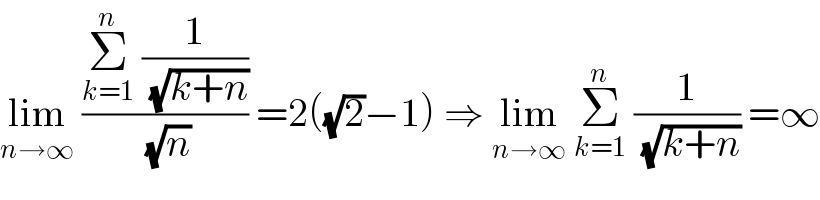
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\mathrm{1}}{\:\sqrt{{k}+{n}}}}{\:\sqrt{{n}}}\:=\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\:\Rightarrow\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\mathrm{1}}{\:\sqrt{{k}+{n}}}\:=\infty \\ $$
Answered by 123564 last updated on 21/Jan/23

