Menu Close

k-1-x-k-1-2-k-1-x-gt-0-

Tinku Tara 0 Comments
Pin




Question Number 100968 by bachamohamed last updated on 29/Jun/20
Σ_(k=1) ^∞ (x+k)^(1/2^(k+1) ) =? x>0
$$\:\:\:\:\:\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\left(\mathrm{x}+\mathrm{k}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}+\mathrm{1}} }} =?\:\:\:\:\:\:\mathrm{x}>\mathrm{0}\: \\ $$
Answered by mathmax by abdo last updated on 29/Jun/20
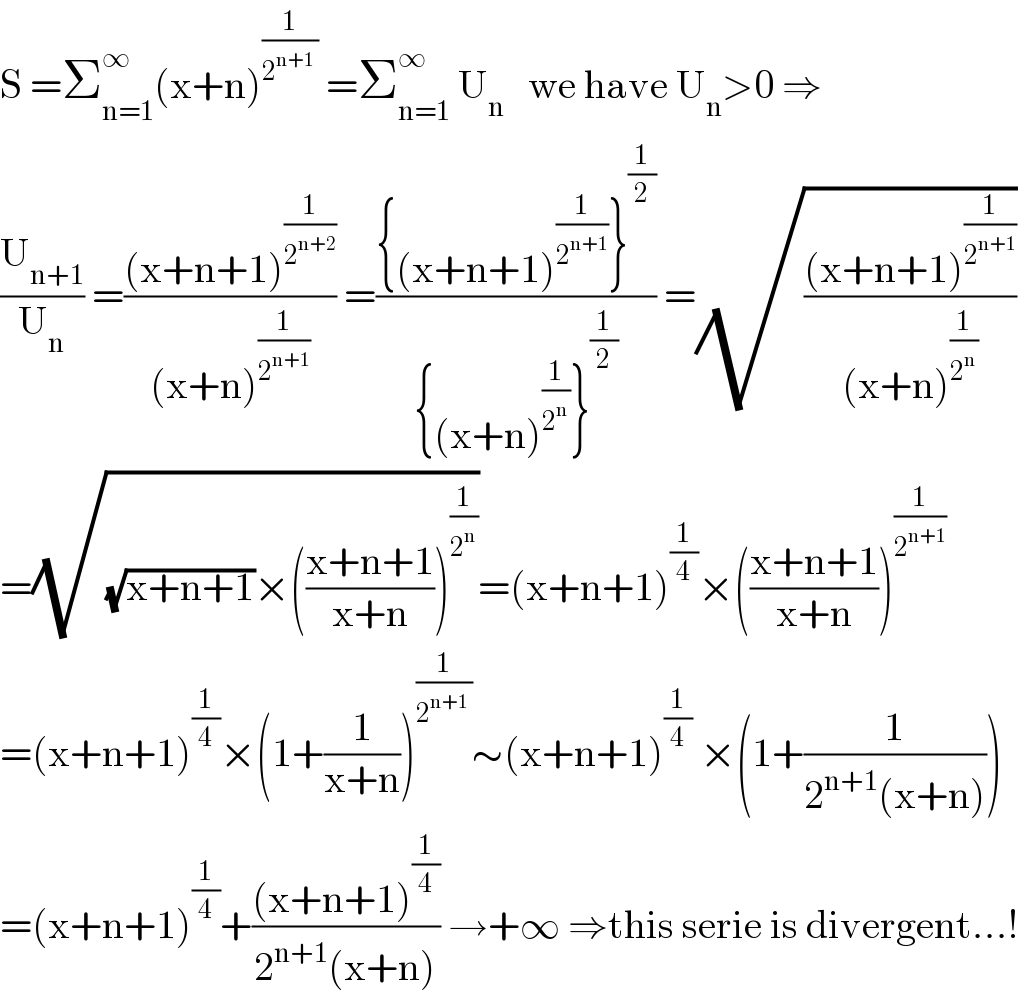
S =Σ_(n=1) ^∞ (x+n)^(1/(2^(n+1) )) =Σ_(n=1) ^∞ U_n we have U_n >0 ⇒ (U_(n+1) /U_n ) =(((x+n+1)^(1/2^(n+2) ) )/((x+n)^(1/2^(n+1) ) )) =(({(x+n+1)^(1/2^(n+1) ) }^(1/2) )/({(x+n)^(1/2^n ) }^(1/2) )) =(√(((x+n+1)^(1/2^(n+1) ) )/((x+n)^(1/2^n ) ))) =(√((√(x+n+1))×(((x+n+1)/(x+n)))^(1/2^n ) ))=(x+n+1)^(1/4) ×(((x+n+1)/(x+n)))^(1/2^(n+1) ) =(x+n+1)^(1/4) ×(1+(1/(x+n)))^(1/(2^(n+1) )) ∼(x+n+1)^(1/4) ×(1+(1/(2^(n+1) (x+n)))) =(x+n+1)^(1/4) +(((x+n+1)^(1/4) )/(2^(n+1) (x+n))) →+∞ ⇒this serie is divergent...!
$$\mathrm{S}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(\mathrm{x}+\mathrm{n}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}+\mathrm{1}} \:}} \:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{U}_{\mathrm{n}} \:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{U}_{\mathrm{n}} >\mathrm{0}\:\Rightarrow \\ $$$$\frac{\mathrm{U}_{\mathrm{n}+\mathrm{1}} }{\mathrm{U}_{\mathrm{n}} }\:=\frac{\left(\mathrm{x}+\mathrm{n}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}+\mathrm{2}} }} }{\left(\mathrm{x}+\mathrm{n}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }} }\:=\frac{\left\{\left(\mathrm{x}+\mathrm{n}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }} \right\}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\left\{\left(\mathrm{x}+\mathrm{n}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }} \right\}^{\frac{\mathrm{1}}{\mathrm{2}}} }\:=\sqrt{\frac{\left(\mathrm{x}+\mathrm{n}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }} }{\left(\mathrm{x}+\mathrm{n}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }} }} \\ $$$$=\sqrt{\sqrt{\mathrm{x}+\mathrm{n}+\mathrm{1}}×\left(\frac{\mathrm{x}+\mathrm{n}+\mathrm{1}}{\mathrm{x}+\mathrm{n}}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }} }=\left(\mathrm{x}+\mathrm{n}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} ×\left(\frac{\mathrm{x}+\mathrm{n}+\mathrm{1}}{\mathrm{x}+\mathrm{n}}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }} \\ $$$$=\left(\mathrm{x}+\mathrm{n}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} ×\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{n}}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}+\mathrm{1}} \:}} \sim\left(\mathrm{x}+\mathrm{n}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \:×\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}+\mathrm{1}} \left(\mathrm{x}+\mathrm{n}\right)}\right) \\ $$$$=\left(\mathrm{x}+\mathrm{n}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} +\frac{\left(\mathrm{x}+\mathrm{n}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }{\mathrm{2}^{\mathrm{n}+\mathrm{1}} \left(\mathrm{x}+\mathrm{n}\right)}\:\rightarrow+\infty\:\Rightarrow\mathrm{this}\:\mathrm{serie}\:\mathrm{is}\:\mathrm{divergent}…! \\ $$
Commented by bachamohamed last updated on 29/Jun/20
thank′s sur but Σ_(k=1) ^n (x+k)^(1/2^(k+1) ) ={(x+1)^(1/2^2 ) +(x+2)^(1/2^3 ) +(x+3)^(1/2^4 ) ......(x+n)^(1/2^(n+1) ) ⇒ Σ_(k=1) ^(k=n) (x+k)^(1/2^(k+1) ) =(√(√((x+1)+(√((x+2)+(x+3)...+.....(√((x+n))))))))=1 ⇒ Σ_(k=1) ^∞ (x+k)^(1/2^(k+1) ) =(√(√((x+1)+(√((x+2)+(√((x+3)+(√((x+4)+........∞)))))))))=1 ⇒ serie is converge pourqoi?
$${thank}'\mathrm{s}\:\mathrm{sur}\:\mathrm{but}\: \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left({x}+{k}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{{k}+\mathrm{1}} }} =\left\{\left({x}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }} +\left({x}+\mathrm{2}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }} +\left({x}+\mathrm{3}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }} ……\left({x}+{n}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} }} \right. \\ $$$$\:\Rightarrow\:\underset{{k}=\mathrm{1}} {\overset{{k}={n}} {\sum}}\left({x}+{k}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{{k}+\mathrm{1}} }} =\sqrt{\sqrt{\left({x}+\mathrm{1}\right)+\sqrt{\left({x}+\mathrm{2}\right)+\left({x}+\mathrm{3}\right)…+…..\sqrt{\left({x}+{n}\right)}}}}=\mathrm{1} \\ $$$$\Rightarrow\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left({x}+{k}\right)^{\frac{\mathrm{1}}{\mathrm{2}^{{k}+\mathrm{1}} }} =\sqrt{\sqrt{\left({x}+\mathrm{1}\right)+\sqrt{\left({x}+\mathrm{2}\right)+\sqrt{\left({x}+\mathrm{3}\right)+\sqrt{\left({x}+\mathrm{4}\right)+……..\infty}}}}}=\mathrm{1}\: \\ $$$$\Rightarrow\:\mathrm{serie}\:\mathrm{is}\:\mathrm{converge}\: \\ $$$${pourqoi}? \\ $$
Commented by maths mind last updated on 29/Jun/20
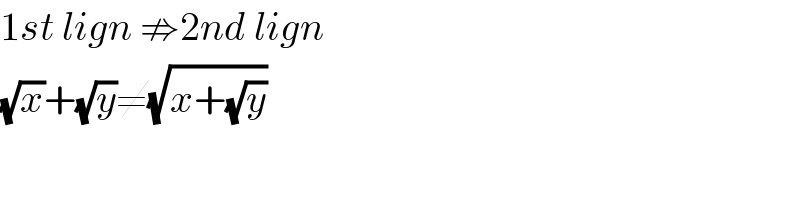
1st lign ⇏2nd lign (√x)+(√y)≠(√(x+(√y)))
$$\mathrm{1}{st}\:{lign}\:\nRightarrow\mathrm{2}{nd}\:{lign} \\ $$$$\sqrt{{x}}+\sqrt{{y}}\neq\sqrt{{x}+\sqrt{{y}}}\:\: \\ $$
Commented by bachamohamed last updated on 29/Jun/20
no it′ s right just look
$$\mathrm{no}\:\mathrm{it}'\:\mathrm{s}\:\mathrm{right}\:\mathrm{just}\:\mathrm{look} \\ $$
Commented by mathmax by abdo last updated on 29/Jun/20
sir you must prove this by recurrence your snswer is not clear...
$$\mathrm{sir}\:\mathrm{you}\:\mathrm{must}\:\mathrm{prove}\:\mathrm{this}\:\mathrm{by}\:\mathrm{recurrence}\:\mathrm{your}\:\mathrm{snswer}\:\mathrm{is}\:\mathrm{not}\:\mathrm{clear}… \\ $$
Answered by mathmax by abdo last updated on 29/Jun/20
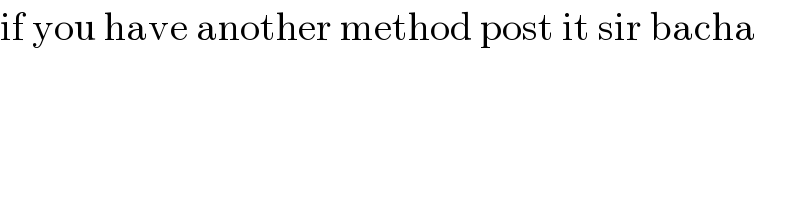
if you have another method post it sir bacha
$$\mathrm{if}\:\mathrm{you}\:\mathrm{have}\:\mathrm{another}\:\mathrm{method}\:\mathrm{post}\:\mathrm{it}\:\mathrm{sir}\:\mathrm{bacha} \\ $$
Commented by bachamohamed last updated on 29/Jun/20
i am looking for other ways becaus i have reached many contradiction so i shared the idea with you
$$\mathrm{i}\:\mathrm{am}\:\mathrm{looking}\:\mathrm{for}\:\mathrm{other}\:\mathrm{ways}\:\mathrm{becaus}\: \\ $$$$\:\mathrm{i}\:\mathrm{have}\:\mathrm{reached}\:\mathrm{many}\:\mathrm{contradiction} \\ $$$$\mathrm{so}\:\mathrm{i}\:\mathrm{shared}\:\mathrm{the}\:\mathrm{idea}\:\mathrm{with}\:\mathrm{you}\: \\ $$
Commented by mathmax by abdo last updated on 30/Jun/20
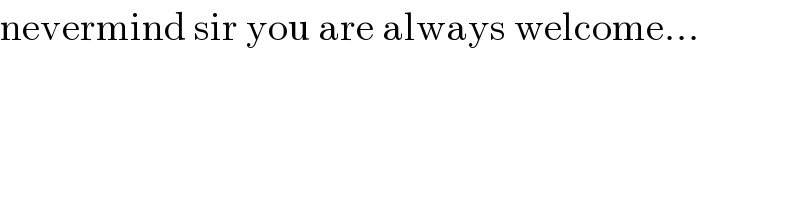
nevermind sir you are always welcome...
$$\mathrm{nevermind}\:\mathrm{sir}\:\mathrm{you}\:\mathrm{are}\:\mathrm{always}\:\mathrm{welcome}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *