Question Number 25973 by soyebshaikh41@gmail.com last updated on 17/Dec/17
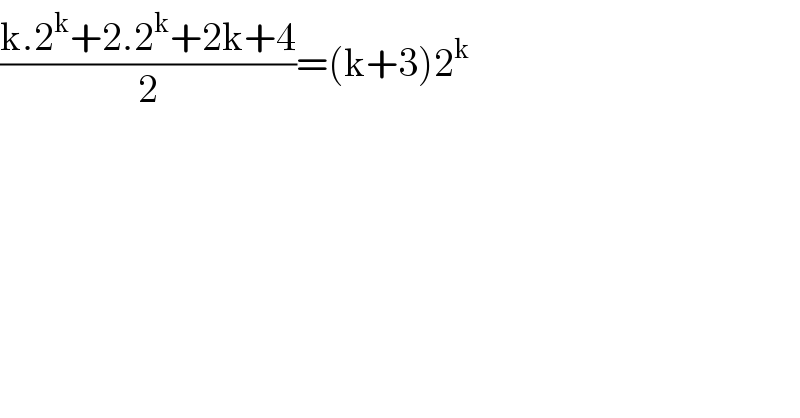
$$\frac{\mathrm{k}.\mathrm{2}^{\mathrm{k}} +\mathrm{2}.\mathrm{2}^{\mathrm{k}} +\mathrm{2k}+\mathrm{4}}{\mathrm{2}}=\left(\mathrm{k}+\mathrm{3}\right)\mathrm{2}^{\mathrm{k}} \\ $$
Answered by prakash jain last updated on 17/Dec/17
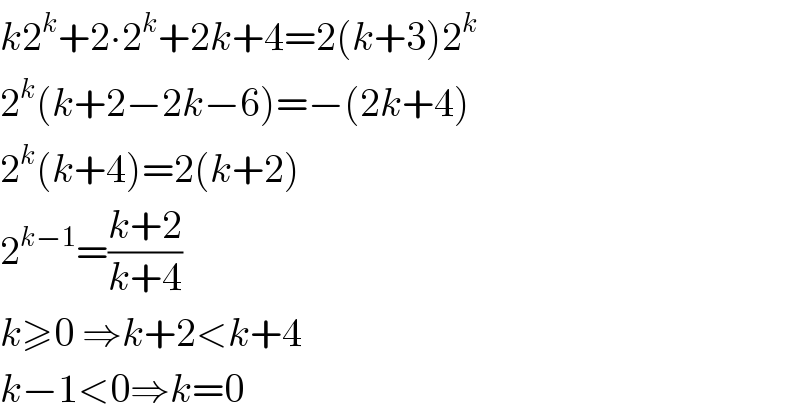
$${k}\mathrm{2}^{{k}} +\mathrm{2}\centerdot\mathrm{2}^{{k}} +\mathrm{2}{k}+\mathrm{4}=\mathrm{2}\left({k}+\mathrm{3}\right)\mathrm{2}^{{k}} \\ $$$$\mathrm{2}^{{k}} \left({k}+\mathrm{2}−\mathrm{2}{k}−\mathrm{6}\right)=−\left(\mathrm{2}{k}+\mathrm{4}\right) \\ $$$$\mathrm{2}^{{k}} \left({k}+\mathrm{4}\right)=\mathrm{2}\left({k}+\mathrm{2}\right) \\ $$$$\mathrm{2}^{{k}−\mathrm{1}} =\frac{{k}+\mathrm{2}}{{k}+\mathrm{4}} \\ $$$${k}\geqslant\mathrm{0}\:\Rightarrow{k}+\mathrm{2}<{k}+\mathrm{4} \\ $$$${k}−\mathrm{1}<\mathrm{0}\Rightarrow{k}=\mathrm{0} \\ $$
