Question Number 165157 by mathlove last updated on 26/Jan/22
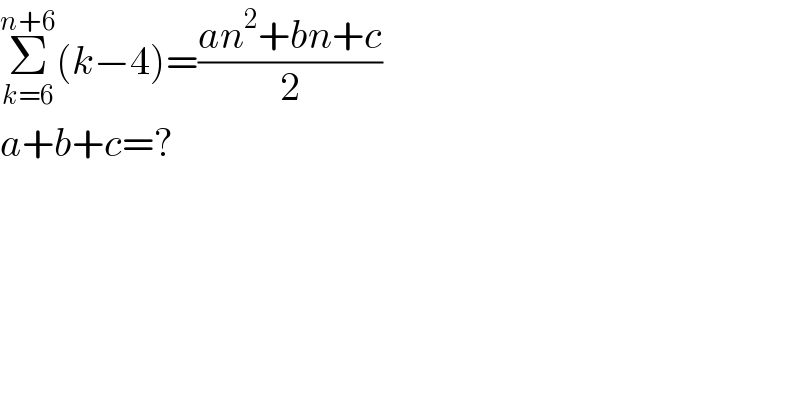
$$\underset{{k}=\mathrm{6}} {\overset{{n}+\mathrm{6}} {\sum}}\left({k}−\mathrm{4}\right)=\frac{{an}^{\mathrm{2}} +{bn}+{c}}{\mathrm{2}} \\ $$$${a}+{b}+{c}=? \\ $$
Commented by bobhans last updated on 30/Jan/22
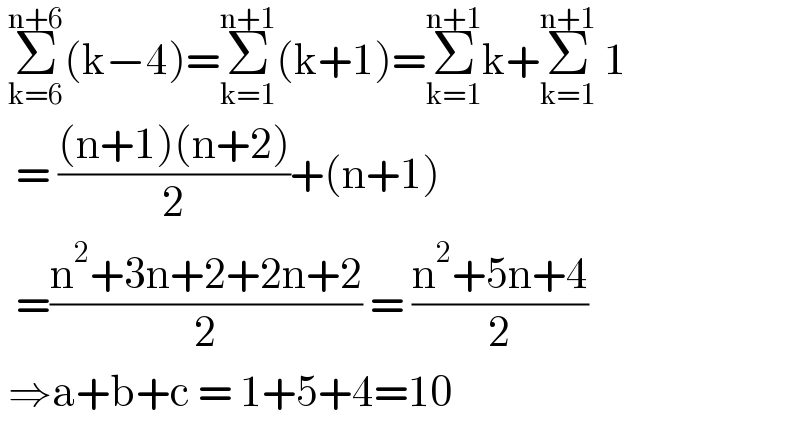
$$\:\underset{\mathrm{k}=\mathrm{6}} {\overset{\mathrm{n}+\mathrm{6}} {\sum}}\left(\mathrm{k}−\mathrm{4}\right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}+\mathrm{1}} {\sum}}\left(\mathrm{k}+\mathrm{1}\right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}+\mathrm{1}} {\sum}}\mathrm{k}+\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}+\mathrm{1}} {\sum}}\:\mathrm{1} \\ $$$$\:\:=\:\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)}{\mathrm{2}}+\left(\mathrm{n}+\mathrm{1}\right) \\ $$$$\:\:=\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{3n}+\mathrm{2}+\mathrm{2n}+\mathrm{2}}{\mathrm{2}}\:=\:\frac{\mathrm{n}^{\mathrm{2}} +\mathrm{5n}+\mathrm{4}}{\mathrm{2}} \\ $$$$\:\Rightarrow\mathrm{a}+\mathrm{b}+\mathrm{c}\:=\:\mathrm{1}+\mathrm{5}+\mathrm{4}=\mathrm{10} \\ $$
Answered by mahdipoor last updated on 26/Jan/22
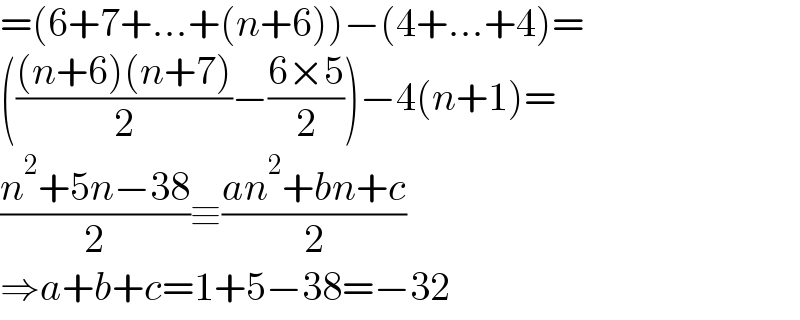
$$=\left(\mathrm{6}+\mathrm{7}+…+\left({n}+\mathrm{6}\right)\right)−\left(\mathrm{4}+…+\mathrm{4}\right)= \\ $$$$\left(\frac{\left({n}+\mathrm{6}\right)\left({n}+\mathrm{7}\right)}{\mathrm{2}}−\frac{\mathrm{6}×\mathrm{5}}{\mathrm{2}}\right)−\mathrm{4}\left({n}+\mathrm{1}\right)= \\ $$$$\frac{{n}^{\mathrm{2}} +\mathrm{5}{n}−\mathrm{38}}{\mathrm{2}}\equiv\frac{{an}^{\mathrm{2}} +{bn}+{c}}{\mathrm{2}} \\ $$$$\Rightarrow{a}+{b}+{c}=\mathrm{1}+\mathrm{5}−\mathrm{38}=−\mathrm{32} \\ $$
Answered by mr W last updated on 30/Jan/22
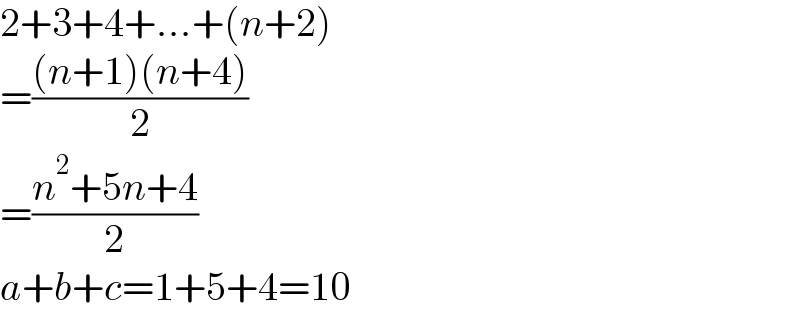
$$\mathrm{2}+\mathrm{3}+\mathrm{4}+…+\left({n}+\mathrm{2}\right) \\ $$$$=\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{4}\right)}{\mathrm{2}} \\ $$$$=\frac{{n}^{\mathrm{2}} +\mathrm{5}{n}+\mathrm{4}}{\mathrm{2}} \\ $$$${a}+{b}+{c}=\mathrm{1}+\mathrm{5}+\mathrm{4}=\mathrm{10} \\ $$
