Menu Close

Knowing-that-k-0-n-n-k-2-2n-n-We-have-p-tokens-and-n-boxes-Each-box-is-labeled-with-a-number-from-1-to-n-Each-box-is-enough-big-to-receive-all-p-tokens-In-how-many

Tinku Tara 0 Comments
Pin




Question Number 125413 by Hassen_Timol last updated on 11/Dec/20
Knowing that : Σ_(k=0) ^n ((n),(k) )^2 = (((2n)),(( n)) ) We have p tokens and n boxes. Each box is labeled with a number from 1 to n. Each box is enough big to receive all p tokens. In how many ways can we share the token : a) if we can distinguish all tokens ? b) if all the tokens are the same ? NB : the boxes may have 0,1,2...,p tokens in them.
$$\mathrm{Knowing}\:\mathrm{that}\:: \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}^{\mathrm{2}} \:=\:\begin{pmatrix}{\mathrm{2}{n}}\\{\:\:{n}}\end{pmatrix} \\ $$$$ \\ $$$$\mathrm{We}\:\mathrm{have}\:{p}\:\mathrm{tokens}\:\mathrm{and}\:{n}\:\mathrm{boxes}. \\ $$$$\mathrm{Each}\:\mathrm{box}\:\mathrm{is}\:\mathrm{labeled}\:\mathrm{with}\:\mathrm{a}\:\mathrm{number}\:\mathrm{from}\:\mathrm{1}\:\mathrm{to}\:{n}. \\ $$$$\mathrm{Each}\:\mathrm{box}\:\mathrm{is}\:\mathrm{enough}\:\mathrm{big}\:\mathrm{to}\:\mathrm{receive}\:\mathrm{all}\:{p}\:\mathrm{tokens}. \\ $$$$ \\ $$$$\mathrm{In}\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{we}\:\mathrm{share}\:\mathrm{the}\:\mathrm{token}\:: \\ $$$$\left.\mathrm{a}\right)\:\:\:\mathrm{if}\:\mathrm{we}\:\mathrm{can}\:\mathrm{distinguish}\:\mathrm{all}\:\mathrm{tokens}\:? \\ $$$$\left.\mathrm{b}\right)\:\:\:\mathrm{if}\:\mathrm{all}\:\mathrm{the}\:\mathrm{tokens}\:\mathrm{are}\:\mathrm{the}\:\mathrm{same}\:? \\ $$$$ \\ $$$$\mathrm{NB}\::\:\mathrm{the}\:\mathrm{boxes}\:\mathrm{may}\:\mathrm{have}\:\mathrm{0},\mathrm{1},\mathrm{2}…,{p}\:\mathrm{tokens}\:\mathrm{in}\:\mathrm{them}. \\ $$
Commented by Hassen_Timol last updated on 10/Dec/20
Could you help me please...?
Answered by mr W last updated on 11/Dec/20
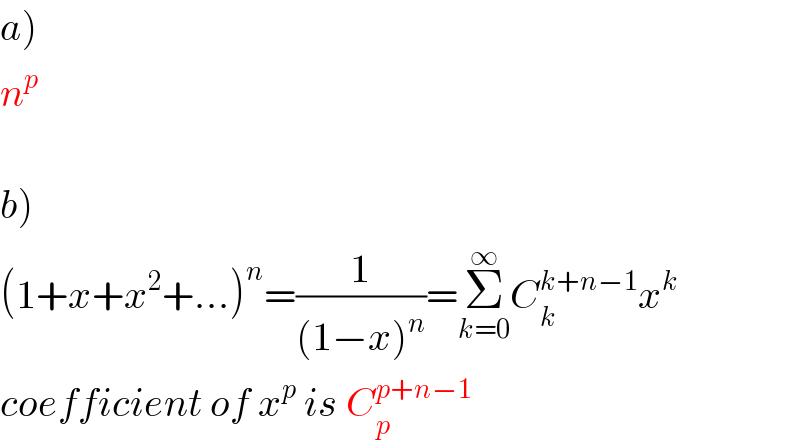
a) n^p b) (1+x+x^2 +...)^n =(1/((1−x)^n ))=Σ_(k=0) ^∞ C_k ^(k+n−1) x^k coefficient of x^p is C_p ^(p+n−1)
$$\left.{a}\right) \\ $$$${n}^{{p}} \\ $$$$ \\ $$$$\left.{b}\right) \\ $$$$\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +…\right)^{{n}} =\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{{n}} }=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{{k}} ^{{k}+{n}−\mathrm{1}} {x}^{{k}} \\ $$$${coefficient}\:{of}\:{x}^{{p}} \:{is}\:{C}_{{p}} ^{{p}+{n}−\mathrm{1}} \\ $$
Commented by Hassen_Timol last updated on 11/Dec/20
Thank you a lot ! I am sorry that I didn't understand but what is x ?
Commented by mr W last updated on 11/Dec/20
i used generating function method. x is here just a symbol for variable. we can also solve (b) using stars & bars method und get C_(n−1) ^(p+n−1) which is the same as C_p ^(p+n−1) .
$${i}\:{used}\:{generating}\:{function}\:{method}. \\ $$$${x}\:{is}\:{here}\:{just}\:{a}\:{symbol}\:{for}\:{variable}. \\ $$$${we}\:{can}\:{also}\:{solve}\:\left({b}\right)\:{using}\:{stars}\:\& \\ $$$${bars}\:{method}\:{und}\:{get}\:{C}_{{n}−\mathrm{1}} ^{{p}+{n}−\mathrm{1}} \:{which} \\ $$$${is}\:{the}\:{same}\:{as}\:{C}_{{p}} ^{{p}+{n}−\mathrm{1}} . \\ $$
Commented by Hassen_Timol last updated on 12/Dec/20
Thank you very much

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *