known-a-lt-pi-2-If-M-lt-1-with-cos-x-cos-y-M-x-y-for-every-x-y-0-a-then-M-

Question Number 55908 by gunawan last updated on 06/Mar/19

known a < \frac{π}{2} .

If M < 1 with ∣ \cos x - \cos y ∣⩽ M ∣ x - y ∣

for every x, y \in [0, a], then M = . .

Answered by tanmay.chaudhury50@gmail.com last updated on 07/Mar/19

l e t y > x

s o c o s x > c o s y

= c o s x - c o s y

= + v e

b u t x - y = - v e

∣ x - y ∣= + v e

f r o m a t t a c h e d g r a p h

t a n θ = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} = \frac{c o s y - c o s x}{y - x}

t a n θ = M = \frac{c o s y - c o s x}{y - x} b u t c o s x > c o s y

y > x s o t a n θ = M i s - v e

w a i t \dots

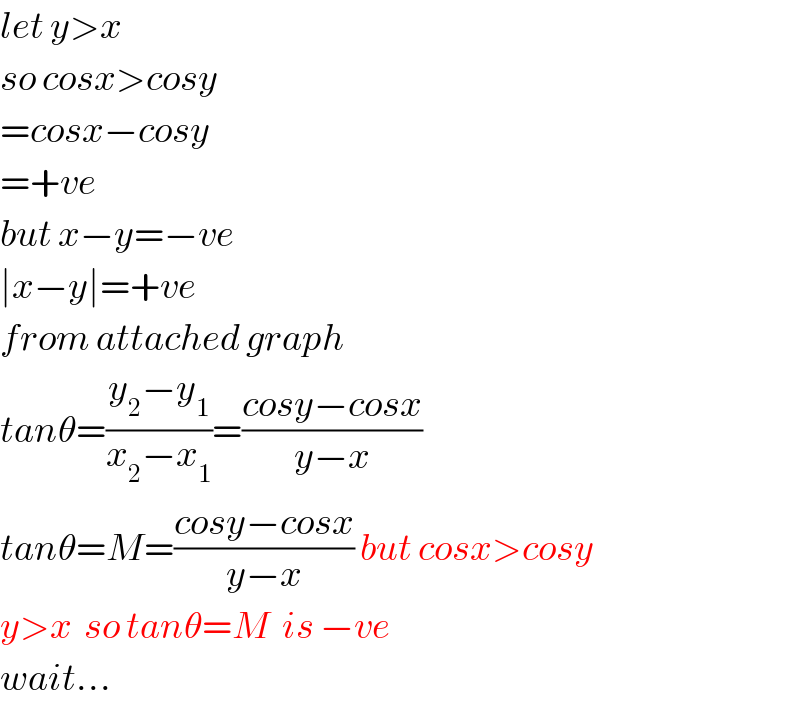
Commented by tanmay.chaudhury50@gmail.com last updated on 07/Mar/19

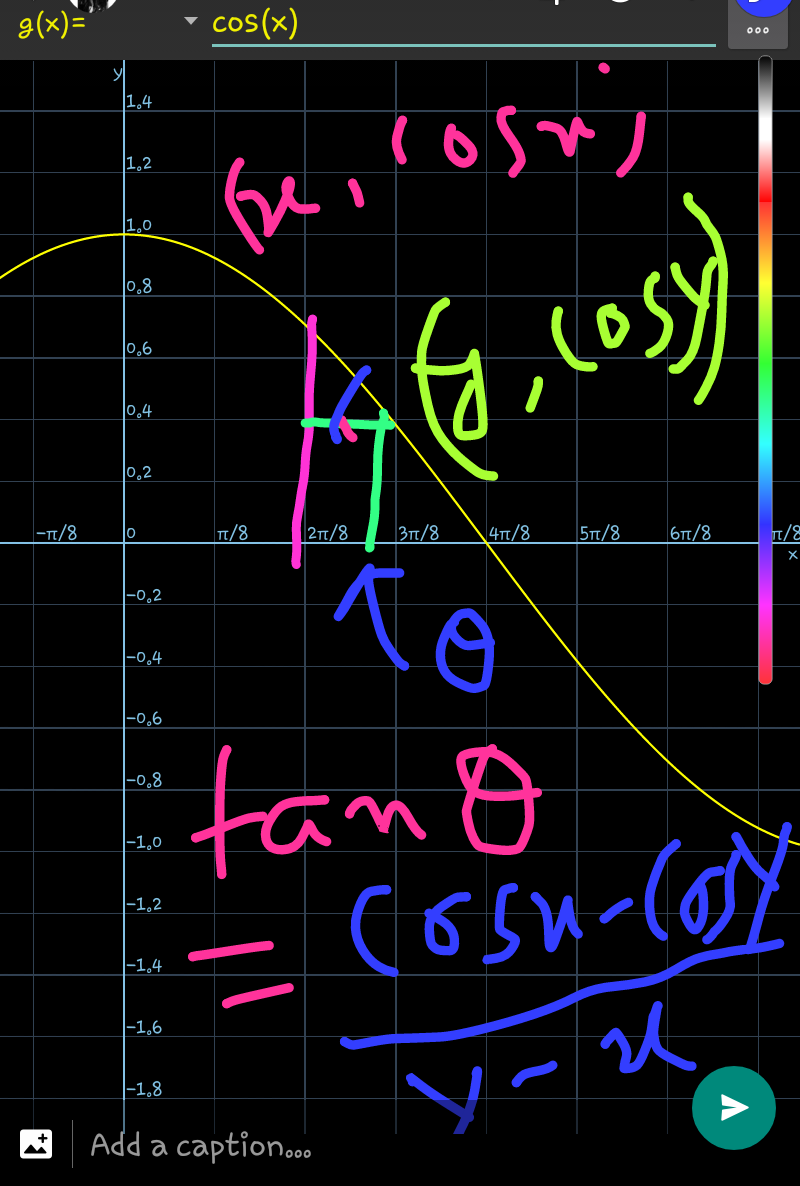
Commented by gunawan last updated on 07/Mar/19

What is the + v e Sir ?

Facebook Tweet Pin