Question Number 55633 by gunawan last updated on 01/Mar/19
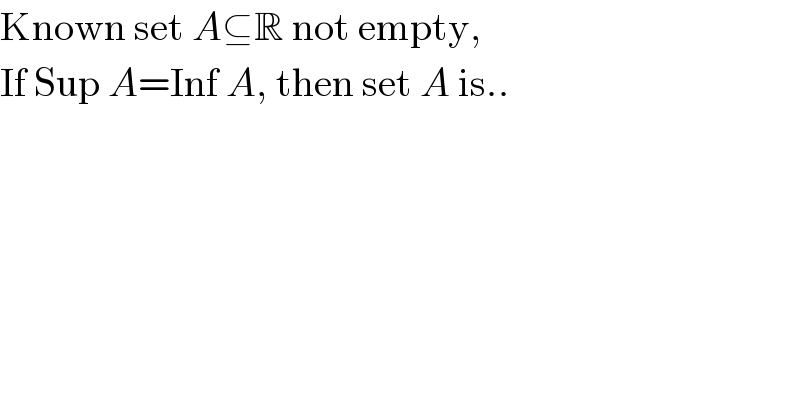
$$\mathrm{Known}\:\mathrm{set}\:{A}\subseteq\mathbb{R}\:\mathrm{not}\:\mathrm{empty}, \\ $$$$\mathrm{If}\:\mathrm{Sup}\:{A}=\mathrm{Inf}\:{A},\:\mathrm{then}\:\mathrm{set}\:{A}\:\mathrm{is}.. \\ $$
Answered by arcana last updated on 18/Jun/19
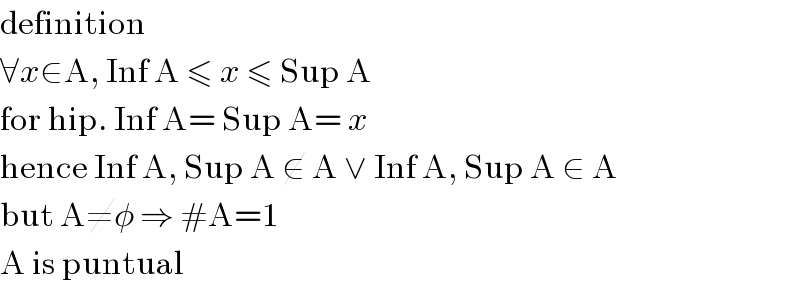
$$\mathrm{definition} \\ $$$$\forall{x}\in\mathrm{A},\:\mathrm{Inf}\:\mathrm{A}\:\leqslant\:{x}\:\leqslant\:\mathrm{Sup}\:\mathrm{A} \\ $$$$\mathrm{for}\:\mathrm{hip}.\:\mathrm{Inf}\:\mathrm{A}=\:\mathrm{Sup}\:\mathrm{A}=\:{x} \\ $$$$\mathrm{hence}\:\mathrm{Inf}\:\mathrm{A},\:\mathrm{Sup}\:\mathrm{A}\:\notin\:\mathrm{A}\:\vee\:\mathrm{Inf}\:\mathrm{A},\:\mathrm{Sup}\:\mathrm{A}\:\in\:\mathrm{A} \\ $$$$\mathrm{but}\:\mathrm{A}\neq\phi\:\Rightarrow\:#\mathrm{A}=\mathrm{1} \\ $$$$\mathrm{A}\:\mathrm{is}\:\mathrm{puntual} \\ $$
