Question Number 155146 by amin96 last updated on 26/Sep/21
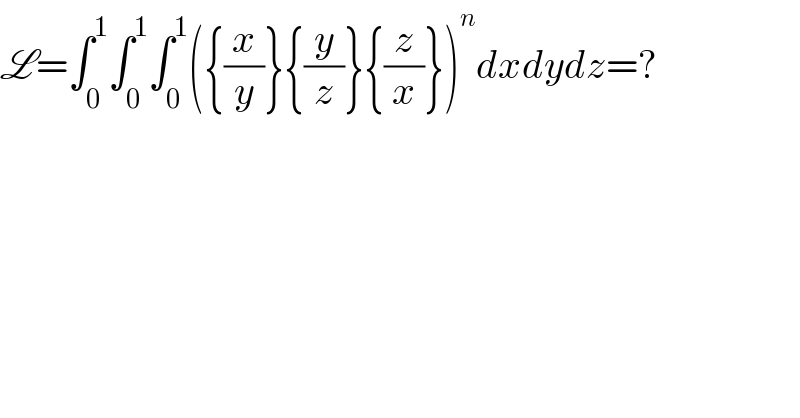
$$\mathscr{L}=\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\left\{\frac{{x}}{{y}}\right\}\left\{\frac{{y}}{{z}}\right\}\left\{\frac{{z}}{{x}}\right\}\right)^{{n}} {dxdydz}=? \\ $$
Answered by yeti123 last updated on 26/Sep/21
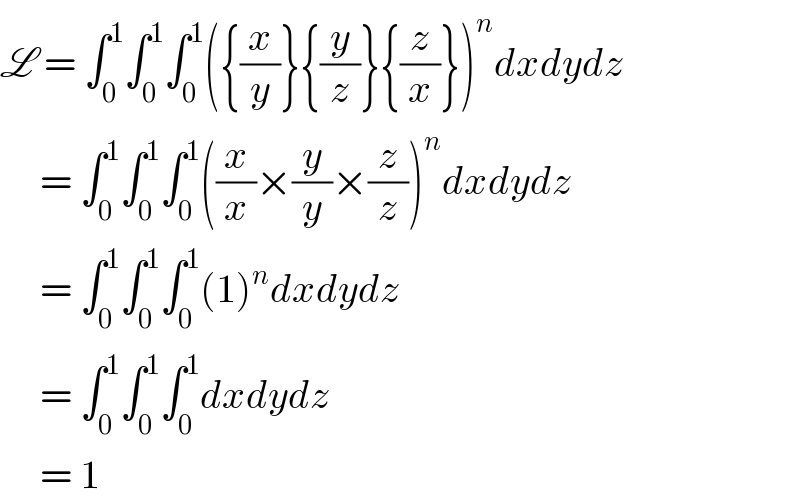
$$\mathscr{L}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\left\{\frac{{x}}{{y}}\right\}\left\{\frac{{y}}{{z}}\right\}\left\{\frac{{z}}{{x}}\right\}\right)^{{n}} {dxdydz} \\ $$$$\:\:\:\:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{{x}}{{x}}×\frac{{y}}{{y}}×\frac{{z}}{{z}}\right)^{{n}} {dxdydz} \\ $$$$\:\:\:\:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}\right)^{{n}} {dxdydz} \\ $$$$\:\:\:\:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} {dxdydz} \\ $$$$\:\:\:\:\:=\:\mathrm{1} \\ $$
