Question Number 129859 by EDWIN88 last updated on 20/Jan/21
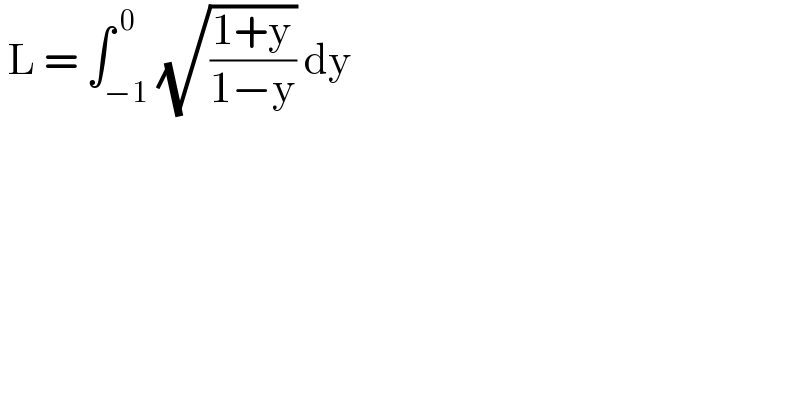
$$\:\mathrm{L}\:=\:\int_{−\mathrm{1}} ^{\:\mathrm{0}} \sqrt{\frac{\mathrm{1}+\mathrm{y}}{\mathrm{1}−\mathrm{y}}}\:\mathrm{dy}\: \\ $$
Answered by liberty last updated on 20/Jan/21
![let y=cos 2t → { ((y=0→t=(π/4))),((y=−1→t=(π/2))) :} L =∫_(π/2) ^( π/4) (√((1+cos 2t)/(1−cos 2t))) (−2sin 2t)dt =−2∫_(π/2) ^( π/4) (√((2cos^2 t)/(2sin^2 t))) (sin 2t)dt =−2∫_(π/2) ^( π/4) ((cos t)/(sin t))(2sin tcos t) dt = −4∫_(π/2) ^( π/4) cos^2 t dt =−4∫_(π/2) ^( π/4) (((1+cos 2t)/2))dt =−2 [ t+(1/2)sin 2t ]_(π/2) ^(π/4) =−2{ (π/4)+(1/2)−(π/2)} =(π/2)−1](https://www.tinkutara.com/question/Q129860.png)
$$\:\mathrm{let}\:\mathrm{y}=\mathrm{cos}\:\mathrm{2t}\:\rightarrow\begin{cases}{\mathrm{y}=\mathrm{0}\rightarrow\mathrm{t}=\frac{\pi}{\mathrm{4}}}\\{\mathrm{y}=−\mathrm{1}\rightarrow\mathrm{t}=\frac{\pi}{\mathrm{2}}}\end{cases} \\ $$$$\mathrm{L}\:=\int_{\pi/\mathrm{2}} ^{\:\pi/\mathrm{4}} \:\sqrt{\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2t}}{\mathrm{1}−\mathrm{cos}\:\mathrm{2t}}}\:\left(−\mathrm{2sin}\:\mathrm{2t}\right)\mathrm{dt} \\ $$$$=−\mathrm{2}\int_{\pi/\mathrm{2}} ^{\:\pi/\mathrm{4}} \:\sqrt{\frac{\mathrm{2cos}\:^{\mathrm{2}} \mathrm{t}}{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{t}}}\:\left(\mathrm{sin}\:\mathrm{2t}\right)\mathrm{dt} \\ $$$$=−\mathrm{2}\int_{\pi/\mathrm{2}} ^{\:\pi/\mathrm{4}} \:\:\frac{\mathrm{cos}\:\mathrm{t}}{\mathrm{sin}\:\mathrm{t}}\left(\mathrm{2sin}\:\mathrm{tcos}\:\mathrm{t}\right)\:\mathrm{dt} \\ $$$$=\:−\mathrm{4}\int_{\pi/\mathrm{2}} ^{\:\pi/\mathrm{4}} \mathrm{cos}\:^{\mathrm{2}} \mathrm{t}\:\mathrm{dt} \\ $$$$=−\mathrm{4}\int_{\pi/\mathrm{2}} ^{\:\pi/\mathrm{4}} \left(\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2t}}{\mathrm{2}}\right)\mathrm{dt} \\ $$$$=−\mathrm{2}\:\left[\:\mathrm{t}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2t}\:\right]_{\pi/\mathrm{2}} ^{\pi/\mathrm{4}} \\ $$$$=−\mathrm{2}\left\{\:\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi}{\mathrm{2}}\right\} \\ $$$$=\frac{\pi}{\mathrm{2}}−\mathrm{1} \\ $$
Answered by Ar Brandon last updated on 20/Jan/21
![L=∫_(−1) ^0 (√((1+y)/(1−y)))dy=∫_(−1) ^0 ((1+y)/( (√(1−y^2 ))))dy =[Arcsin(y)−(√(1−y^2 ))]_(−1) ^0 =(π/2)−1](https://www.tinkutara.com/question/Q129888.png)
$$\mathrm{L}=\int_{−\mathrm{1}} ^{\mathrm{0}} \sqrt{\frac{\mathrm{1}+\mathrm{y}}{\mathrm{1}−\mathrm{y}}}\mathrm{dy}=\int_{−\mathrm{1}} ^{\mathrm{0}} \frac{\mathrm{1}+\mathrm{y}}{\:\sqrt{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }}\mathrm{dy} \\ $$$$\:\:\:=\left[\mathrm{Arcsin}\left(\mathrm{y}\right)−\sqrt{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }\right]_{−\mathrm{1}} ^{\mathrm{0}} =\frac{\pi}{\mathrm{2}}−\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 20/Jan/21
![L=∫_(−1) ^0 (√((1+y)/(1−y)))dy we do the changement (√((1+y)/(1−y)))=x ⇒((1+y)/(1−y))=x^2 ⇒ 1+y=x^2 −x^2 y ⇒(1+x^2 )y=x^2 −1 ⇒y=((x^2 −1)/(x^2 +1)) ⇒ (dy/dx)=((2x(x^2 +1)−2x(x^2 −1))/((x^2 +1)^2 ))=((4x)/((x^2 +1)^2 )) ⇒ L=∫_0 ^1 x.((4x)/((x^2 +1)^2 ))dx =4∫_0 ^1 ((x^2 +1−1)/((x^2 +1)^2 ))dx=4∫_0 ^1 (dx/(x^2 +1))−4∫_0 ^1 (dx/((x^2 +1)^2 )) we have ∫_0 ^1 (dx/(x^2 +1))=[arctanx]_0 ^1 =(π/4) ∫_0 ^1 (dx/((x^2 +1)^2 ))=_(x=tanθ) ∫_0 ^(π/4) (((1+tan^2 θ))/((1+tan^2 θ)^2 ))dθ =∫_0 ^(π/4) (dθ/(1+tan^2 θ)) =∫_0 ^(π/4) cos^2 θ dθ =∫_0 ^(π/4) ((1+cos(2θ))/2)dθ =(π/8) +[(1/4)sin(2θ)]_0 ^(π/4) =(π/8)+(1/4) ⇒L=π−4((π/8)+(1/4))=π−(π/2)−1 =(π/2)−1](https://www.tinkutara.com/question/Q129930.png)
$$\mathrm{L}=\int_{−\mathrm{1}} ^{\mathrm{0}} \sqrt{\frac{\mathrm{1}+\mathrm{y}}{\mathrm{1}−\mathrm{y}}}\mathrm{dy}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\sqrt{\frac{\mathrm{1}+\mathrm{y}}{\mathrm{1}−\mathrm{y}}}=\mathrm{x}\:\Rightarrow\frac{\mathrm{1}+\mathrm{y}}{\mathrm{1}−\mathrm{y}}=\mathrm{x}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{1}+\mathrm{y}=\mathrm{x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} \mathrm{y}\:\Rightarrow\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{y}=\mathrm{x}^{\mathrm{2}} −\mathrm{1}\:\Rightarrow\mathrm{y}=\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{2x}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{2x}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{4x}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{L}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}.\frac{\mathrm{4x}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{1}}{\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\boldsymbol{\mathrm{dx}}=\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}−\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{we}\:\mathrm{have}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}=\left[\mathrm{arctanx}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\pi}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }=_{\mathrm{x}=\mathrm{tan}\theta} \:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)}{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }\mathrm{d}\theta\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{d}\theta}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{cos}^{\mathrm{2}} \theta\:\mathrm{d}\theta\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}\mathrm{d}\theta\:=\frac{\pi}{\mathrm{8}}\:+\left[\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\frac{\pi}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\mathrm{L}=\pi−\mathrm{4}\left(\frac{\pi}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{4}}\right)=\pi−\frac{\pi}{\mathrm{2}}−\mathrm{1}\:=\frac{\pi}{\mathrm{2}}−\mathrm{1} \\ $$
