Question Number 27293 by sorour87 last updated on 04/Jan/18
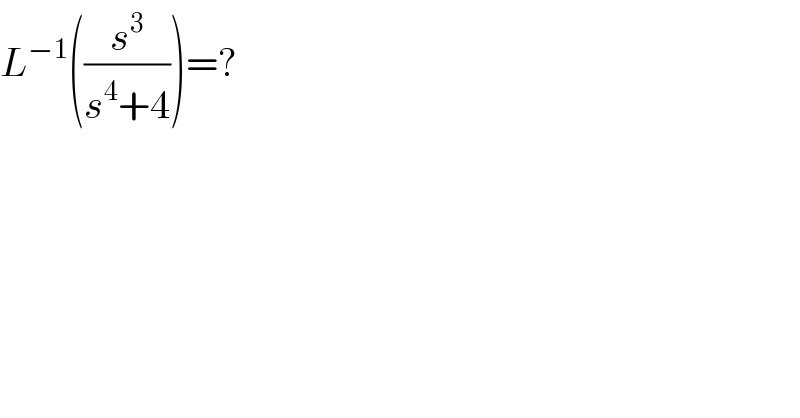
$${L}^{−\mathrm{1}} \left(\frac{{s}^{\mathrm{3}} }{{s}^{\mathrm{4}} +\mathrm{4}}\right)=? \\ $$
Answered by sma3l2996 last updated on 04/Jan/18
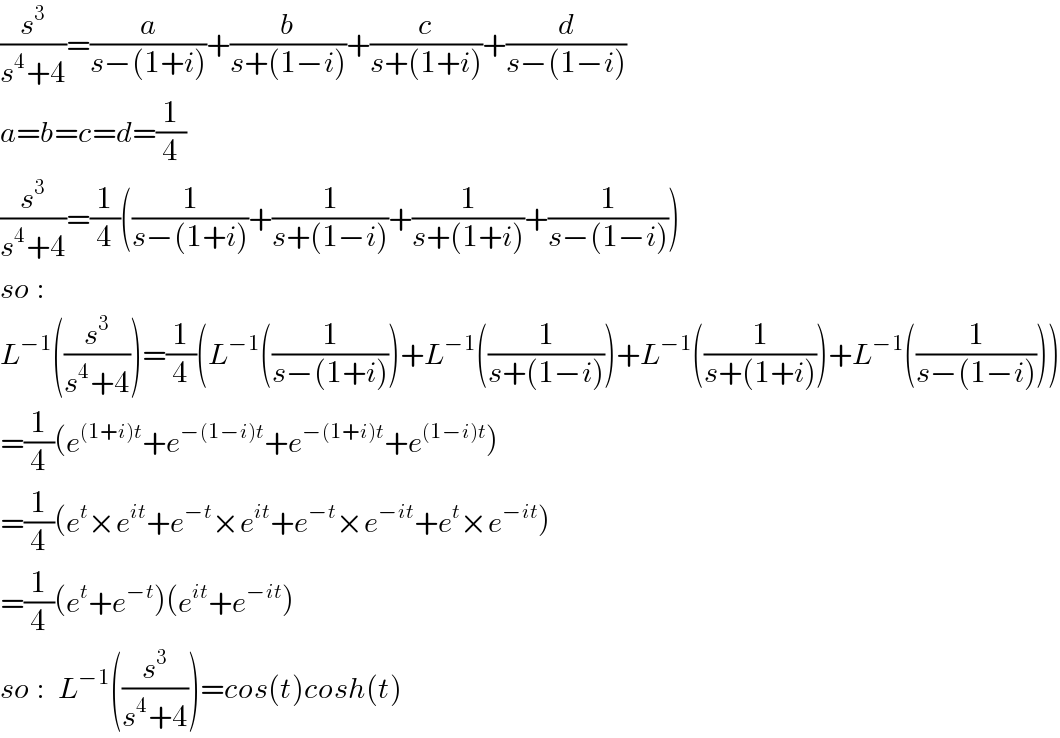
$$\frac{{s}^{\mathrm{3}} }{{s}^{\mathrm{4}} +\mathrm{4}}=\frac{{a}}{{s}−\left(\mathrm{1}+{i}\right)}+\frac{{b}}{{s}+\left(\mathrm{1}−{i}\right)}+\frac{{c}}{{s}+\left(\mathrm{1}+{i}\right)}+\frac{{d}}{{s}−\left(\mathrm{1}−{i}\right)} \\ $$$${a}={b}={c}={d}=\frac{\mathrm{1}}{\mathrm{4}}\: \\ $$$$\frac{{s}^{\mathrm{3}} }{{s}^{\mathrm{4}} +\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{{s}−\left(\mathrm{1}+{i}\right)}+\frac{\mathrm{1}}{{s}+\left(\mathrm{1}−{i}\right)}+\frac{\mathrm{1}}{{s}+\left(\mathrm{1}+{i}\right)}+\frac{\mathrm{1}}{{s}−\left(\mathrm{1}−{i}\right)}\right) \\ $$$${so}\:: \\ $$$${L}^{−\mathrm{1}} \left(\frac{{s}^{\mathrm{3}} }{{s}^{\mathrm{4}} +\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left({L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{s}−\left(\mathrm{1}+{i}\right)}\right)+{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{s}+\left(\mathrm{1}−{i}\right)}\right)+{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{s}+\left(\mathrm{1}+{i}\right)}\right)+{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{s}−\left(\mathrm{1}−{i}\right)}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left({e}^{\left(\mathrm{1}+{i}\right){t}} +{e}^{−\left(\mathrm{1}−{i}\right){t}} +{e}^{−\left(\mathrm{1}+{i}\right){t}} +{e}^{\left(\mathrm{1}−{i}\right){t}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left({e}^{{t}} ×{e}^{{it}} +{e}^{−{t}} ×{e}^{{it}} +{e}^{−{t}} ×{e}^{−{it}} +{e}^{{t}} ×{e}^{−{it}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left({e}^{{t}} +{e}^{−{t}} \right)\left({e}^{{it}} +{e}^{−{it}} \right) \\ $$$${so}\::\:\:{L}^{−\mathrm{1}} \left(\frac{{s}^{\mathrm{3}} }{{s}^{\mathrm{4}} +\mathrm{4}}\right)={cos}\left({t}\right){cosh}\left({t}\right) \\ $$
