Menu Close

L-lim-n-1-1-2-2-1-1-2-2-2n-1-n-2-2n-

Tinku Tara 0 Comments
Pin




Question Number 144380 by SOMEDAVONG last updated on 25/Jun/21
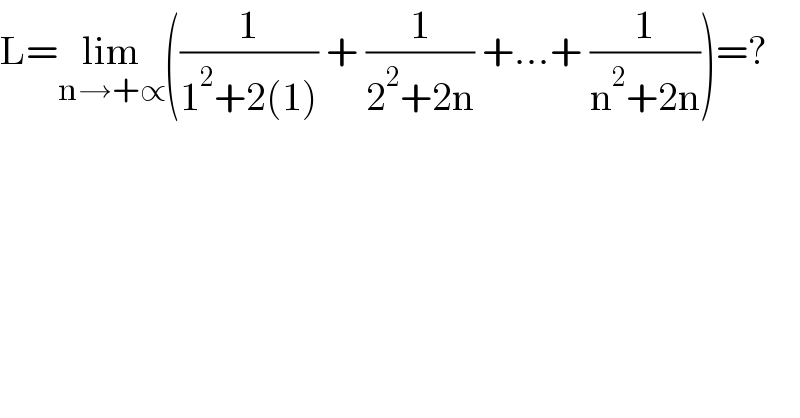
L=lim_(n→+∝) ((1/(1^2 +2(1))) + (1/(2^2 +2n)) +...+ (1/(n^2 +2n)))=?
$$\mathrm{L}=\underset{\mathrm{n}\rightarrow+\propto} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{1}\right)}\:+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} +\mathrm{2n}}\:+…+\:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} +\mathrm{2n}}\right)=? \\ $$
Answered by mathmax by abdo last updated on 25/Jun/21
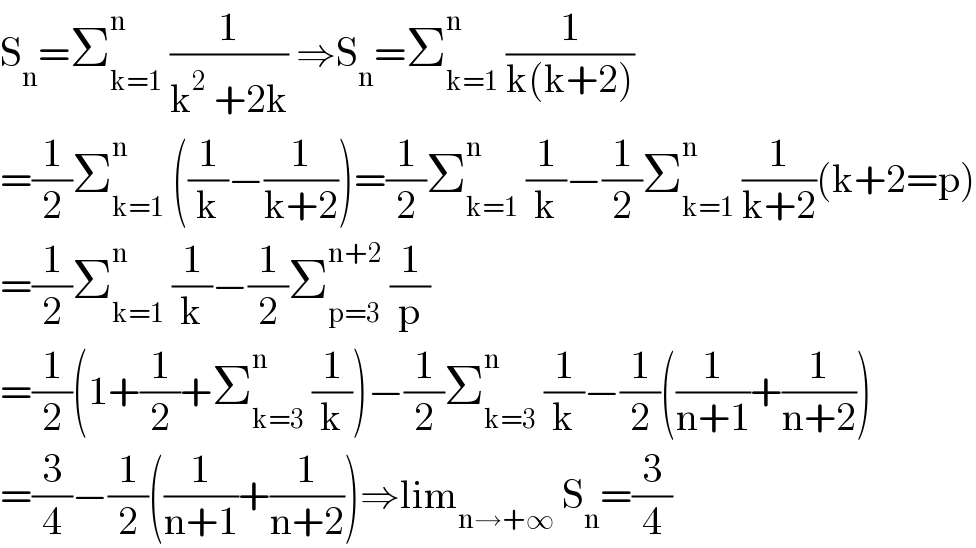
S_n =Σ_(k=1) ^n (1/(k^2 +2k)) ⇒S_n =Σ_(k=1) ^(n ) (1/(k(k+2))) =(1/2)Σ_(k=1) ^n ((1/k)−(1/(k+2)))=(1/2)Σ_(k=1) ^n (1/k)−(1/2)Σ_(k=1) ^n (1/(k+2))(k+2=p) =(1/2)Σ_(k=1) ^n (1/k)−(1/2)Σ_(p=3) ^(n+2) (1/p) =(1/2)(1+(1/2)+Σ_(k=3) ^n (1/k))−(1/2)Σ_(k=3) ^n (1/k)−(1/2)((1/(n+1))+(1/(n+2))) =(3/4)−(1/2)((1/(n+1))+(1/(n+2)))⇒lim_(n→+∞) S_n =(3/4)
$$\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} \:+\mathrm{2k}}\:\Rightarrow\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}\:} \:\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{k}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\left(\frac{\mathrm{1}}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{k}+\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{2}}\left(\mathrm{k}+\mathrm{2}=\mathrm{p}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{p}=\mathrm{3}} ^{\mathrm{n}+\mathrm{2}} \:\frac{\mathrm{1}}{\mathrm{p}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\sum_{\mathrm{k}=\mathrm{3}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{3}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right)\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{S}_{\mathrm{n}} =\frac{\mathrm{3}}{\mathrm{4}} \\ $$
Commented by SOMEDAVONG last updated on 25/Jun/21
Thanks sir!
$$\mathrm{Thanks}\:\mathrm{sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *