Menu Close

L-lim-x-0-2sin-x-2tan-x-x-3-6x-2sin-3x-9x-3-L-lim-x-0-2sin-x-2tan-x-x-3-x-5-lim-x-0-6x-2sin-3x-9x-3-x-5-L-1-L-2-

Tinku Tara 0 Comments
Pin




Question Number 183485 by Gamil last updated on 26/Dec/22
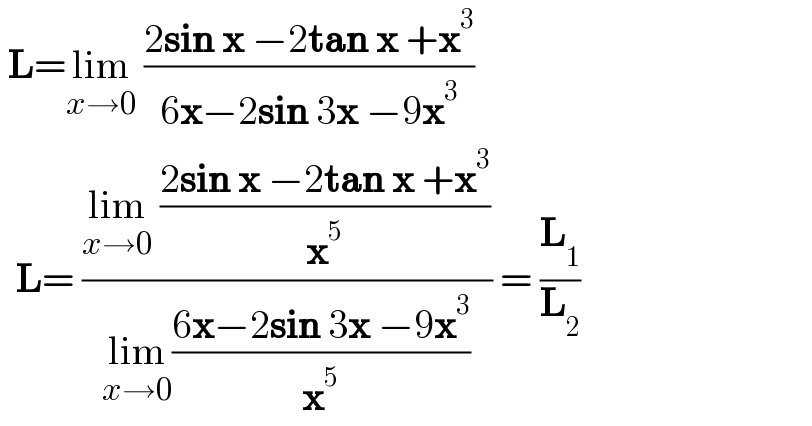
L=lim_(x→0) ((2sin x −2tan x +x^3 )/(6x−2sin 3x −9x^3 )) L= ((lim_(x→0) ((2sin x −2tan x +x^3 )/x^5 ))/(lim_(x→0) ((6x−2sin 3x −9x^3 )/x^5 ))) = (L_1 /L_2 )
$$\:\boldsymbol{\mathrm{L}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\boldsymbol{\mathrm{sin}}\:\boldsymbol{\mathrm{x}}\:−\mathrm{2}\boldsymbol{\mathrm{tan}}\:\boldsymbol{\mathrm{x}}\:+\boldsymbol{\mathrm{x}}^{\mathrm{3}} }{\mathrm{6}\boldsymbol{\mathrm{x}}−\mathrm{2}\boldsymbol{\mathrm{sin}}\:\mathrm{3}\boldsymbol{\mathrm{x}}\:−\mathrm{9}\boldsymbol{\mathrm{x}}^{\mathrm{3}} } \\ $$$$\:\:\boldsymbol{\mathrm{L}}=\:\frac{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\boldsymbol{\mathrm{sin}}\:\boldsymbol{\mathrm{x}}\:−\mathrm{2}\boldsymbol{\mathrm{tan}}\:\boldsymbol{\mathrm{x}}\:+\boldsymbol{\mathrm{x}}^{\mathrm{3}} }{\boldsymbol{\mathrm{x}}^{\mathrm{5}} }}{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{6}\boldsymbol{\mathrm{x}}−\mathrm{2}\boldsymbol{\mathrm{sin}}\:\mathrm{3}\boldsymbol{\mathrm{x}}\:−\mathrm{9}\boldsymbol{\mathrm{x}}^{\mathrm{3}} }{\boldsymbol{\mathrm{x}}^{\mathrm{5}} }}\:=\:\frac{\boldsymbol{\mathrm{L}}_{\mathrm{1}} }{\boldsymbol{\mathrm{L}}_{\mathrm{2}} } \\ $$
Commented by CElcedricjunior last updated on 26/Dec/22
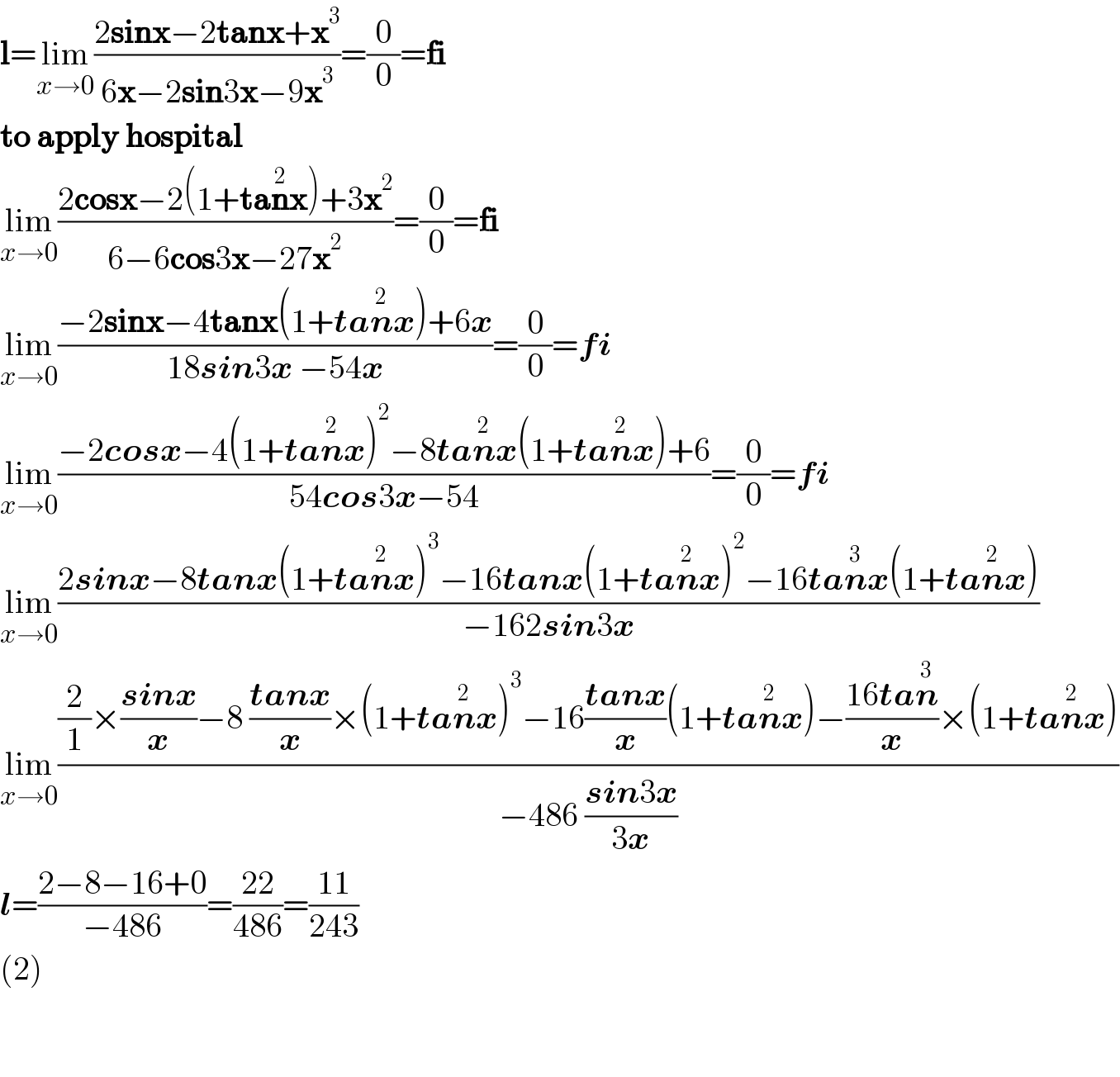
l=lim_(x→0) ((2sinx−2tanx+x^3 )/(6x−2sin3x−9x^3 ))=(0/0)=fi to apply hospital lim_(x→0) ((2cosx−2(1+tan^2 x)+3x^2 )/(6−6cos3x−27x^2 ))=(0/0)=fi lim_(x→0) ((−2sinx−4tanx(1+tan^2 x)+6x)/(18sin3x −54x))=(0/0)=fi lim_(x→0) ((−2cosx−4(1+tan^2 x)^2 −8tan^2 x(1+tan^2 x)+6)/(54cos3x−54))=(0/0)=fi lim_(x→0) ((2sinx−8tanx(1+tan^2 x)^3 −16tanx(1+tan^2 x)^2 −16tan^3 x(1+tan^2 x))/(−162sin3x)) lim_(x→0) (((2/1)×((sinx)/x)−8 ((tanx)/x)×(1+tan^2 x)^3 −16((tanx)/x)(1+tan^2 x)−((16tan^3 )/x)×(1+tan^2 x))/(−486 ((sin3x)/(3x)))) l=((2−8−16+0)/(−486))=((22)/(486))=((11)/(243)) (2)
$$\boldsymbol{\mathrm{l}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\boldsymbol{\mathrm{sinx}}−\mathrm{2}\boldsymbol{\mathrm{tanx}}+\boldsymbol{\mathrm{x}}^{\mathrm{3}} }{\mathrm{6}\boldsymbol{\mathrm{x}}−\mathrm{2}\boldsymbol{\mathrm{sin}}\mathrm{3}\boldsymbol{\mathrm{x}}−\mathrm{9}\boldsymbol{\mathrm{x}}^{\mathrm{3}} }=\frac{\mathrm{0}}{\mathrm{0}}=\boldsymbol{\mathrm{fi}} \\ $$$$\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{apply}}\:\boldsymbol{\mathrm{hospital}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\boldsymbol{\mathrm{cosx}}−\mathrm{2}\left(\mathrm{1}+\boldsymbol{\mathrm{ta}}\overset{\mathrm{2}} {\boldsymbol{\mathrm{n}x}}\right)+\mathrm{3}\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\mathrm{6}−\mathrm{6}\boldsymbol{\mathrm{cos}}\mathrm{3}\boldsymbol{\mathrm{x}}−\mathrm{27}\boldsymbol{\mathrm{x}}^{\mathrm{2}} }=\frac{\mathrm{0}}{\mathrm{0}}=\boldsymbol{\mathrm{fi}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2}\boldsymbol{\mathrm{sinx}}−\mathrm{4}\boldsymbol{\mathrm{tanx}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)+\mathrm{6}\boldsymbol{{x}}}{\mathrm{18}\boldsymbol{{sin}}\mathrm{3}\boldsymbol{{x}}\:−\mathrm{54}\boldsymbol{{x}}}=\frac{\mathrm{0}}{\mathrm{0}}=\boldsymbol{{fi}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2}\boldsymbol{{cosx}}−\mathrm{4}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)^{\mathrm{2}} −\mathrm{8}\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)+\mathrm{6}}{\mathrm{54}\boldsymbol{{cos}}\mathrm{3}\boldsymbol{{x}}−\mathrm{54}}=\frac{\mathrm{0}}{\mathrm{0}}=\boldsymbol{{fi}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\boldsymbol{{sinx}}−\mathrm{8}\boldsymbol{{tanx}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)^{\mathrm{3}} −\mathrm{16}\boldsymbol{{tanx}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)^{\mathrm{2}} −\mathrm{16}\boldsymbol{{ta}}\overset{\mathrm{3}} {\boldsymbol{{n}x}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)}{−\mathrm{162}\boldsymbol{{sin}}\mathrm{3}\boldsymbol{{x}}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{2}}{\mathrm{1}}×\frac{\boldsymbol{{sinx}}}{\boldsymbol{{x}}}−\mathrm{8}\:\frac{\boldsymbol{{tanx}}}{\boldsymbol{{x}}}×\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)^{\mathrm{3}} −\mathrm{16}\frac{\boldsymbol{{tanx}}}{\boldsymbol{{x}}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)−\frac{\mathrm{16}\boldsymbol{{ta}}\overset{\mathrm{3}} {\boldsymbol{{n}}}}{\boldsymbol{{x}}}×\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)}{−\mathrm{486}\:\frac{\boldsymbol{{sin}}\mathrm{3}\boldsymbol{{x}}}{\mathrm{3}\boldsymbol{{x}}}} \\ $$$$\boldsymbol{{l}}=\frac{\mathrm{2}−\mathrm{8}−\mathrm{16}+\mathrm{0}}{−\mathrm{486}}=\frac{\mathrm{22}}{\mathrm{486}}=\frac{\mathrm{11}}{\mathrm{243}} \\ $$$$\left(\mathrm{2}\right) \\ $$$$ \\ $$$$ \\ $$
Answered by CElcedricjunior last updated on 26/Dec/22
l=((lim_(x→0) ((2sinx−2tanx+x^3 )/x^5 ))/(lim_(x→0) ((6x−2sin3x−9x^3 )/x^5 ))) =lim_(x→0) ((2sinx−2tanx+x^3 )/(6x−2sin3x−9x^3 ))=(0/0)fi to apply hospital =lim_(x→0) ((2cosx−2(1+tan^2 x)+3x^2 )/(6−6cos3x−27x^2 ))=(0/0)fi =lim_(x→0) ((−2sinx−4tanx(1+tan^2 x)+6x)/(+18sin3x−54x))=(0/0) fi =lim_(x→0) ((−2cosx−4(1+tan^2 x)^2 −8tan^2 (1+tan^2 x)+6)/(54cos3x−54))=(0/0)=fi =lim_(x→0) ((2sinx−8tanx(1+tan^2 x)^2 −16tan(1+tan^2 x)^2 −16tan^2 (1+tan^2 x))/(−164sin3x)) =lim_(x→0) ((2((sinx)/x)−8((tanx)/x)(1+tan^2 x)−16((tanx)/x)(1+tan^2 x)^2 −16((tan^2 x)/x)(1+tan^2 x))/(−492((sin3x)/(3x)))) l=((2−8−16)/(−492))=((22)/(492))=((11)/(246)) l=((lim_(x→0) ((2sinx−2tanx+x^3 )/x^5 ))/(lim_(x→0) ((6x−2sin3x−9x^3 )/x^5 ))) =lim_(x→0) ((2sinx−2tanx+x^3 )/(6x−2sin3x−9x^3 ))=(0/0)fi to apply hospital =lim_(x→0) ((2cosx−2(1+tan^2 x)+3x^2 )/(6−6cos3x−27x^2 ))=(0/0)fi =lim_(x→0) ((−2sinx−4tanx(1+tan^2 x)+6x)/(+18sin3x−54x))=(0/0) fi =lim_(x→0) ((−2cosx−4(1+tan^2 x)^2 −8tan^2 (1+tan^2 x)+6)/(54cos3x−54))=(0/0)=fi =lim_(x→0) ((2sinx−8tanx(1+tan^2 x)^2 −16tan(1+tan^2 x)^2 −16tan^2 (1+tan^2 x))/(−164sin3x)) =lim_(x→0) ((2((sinx)/x)−8((tanx)/x)(1+tan^2 x)−16((tanx)/x)(1+tan^2 x)^2 −16((tan^2 x)/x)(1+tan^2 x))/(−492((sin3x)/(3x)))) l=((2−8−16)/(−492))=((22)/(492))=((11)/(246)) l> l>
$$\boldsymbol{{l}}=\frac{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\boldsymbol{{sinx}}−\mathrm{2}\boldsymbol{{tanx}}+\boldsymbol{{x}}^{\mathrm{3}} }{\boldsymbol{{x}}^{\mathrm{5}} }}{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{6}\boldsymbol{{x}}−\mathrm{2}\boldsymbol{{sin}}\mathrm{3}\boldsymbol{{x}}−\mathrm{9}\boldsymbol{{x}}^{\mathrm{3}} }{\boldsymbol{{x}}^{\mathrm{5}} }} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\boldsymbol{{sinx}}−\mathrm{2}\boldsymbol{{tanx}}+\boldsymbol{{x}}^{\mathrm{3}} }{\mathrm{6}\boldsymbol{{x}}−\mathrm{2}\boldsymbol{{sin}}\mathrm{3}\boldsymbol{{x}}−\mathrm{9}\boldsymbol{{x}}^{\mathrm{3}} }=\frac{\mathrm{0}}{\mathrm{0}}\boldsymbol{{fi}} \\ $$$$\boldsymbol{{to}}\:\boldsymbol{{apply}}\:\boldsymbol{{hospital}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\boldsymbol{{cosx}}−\mathrm{2}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)+\mathrm{3}\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{6}−\mathrm{6}\boldsymbol{{cos}}\mathrm{3}\boldsymbol{{x}}−\mathrm{27}\overset{\mathrm{2}} {\boldsymbol{{x}}}}=\frac{\mathrm{0}}{\mathrm{0}}\boldsymbol{{fi}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2}\boldsymbol{{sinx}}−\mathrm{4}\boldsymbol{{tanx}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)+\mathrm{6}\boldsymbol{{x}}}{+\mathrm{18}\boldsymbol{{sin}}\mathrm{3}\boldsymbol{{x}}−\mathrm{54}\boldsymbol{{x}}}=\frac{\mathrm{0}}{\mathrm{0}}\:\boldsymbol{{fi}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2}\boldsymbol{{cosx}}−\mathrm{4}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)^{\mathrm{2}} −\mathrm{8}\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)+\mathrm{6}}{\mathrm{54}\boldsymbol{{cos}}\mathrm{3}\boldsymbol{{x}}−\mathrm{54}}=\frac{\mathrm{0}}{\mathrm{0}}=\boldsymbol{{fi}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\boldsymbol{{sinx}}−\mathrm{8}\boldsymbol{{tanx}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)^{\mathrm{2}} −\mathrm{16}\boldsymbol{{tan}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)^{\mathrm{2}} −\mathrm{16}\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)}{−\mathrm{164}\boldsymbol{{sin}}\mathrm{3}\boldsymbol{{x}}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\frac{\boldsymbol{{sinx}}}{\boldsymbol{{x}}}−\mathrm{8}\frac{\boldsymbol{{tanx}}}{\boldsymbol{{x}}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)−\mathrm{16}\frac{\boldsymbol{{tanx}}}{\boldsymbol{{x}}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)^{\mathrm{2}} −\mathrm{16}\frac{\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}}{\boldsymbol{{x}}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)}{−\mathrm{492}\frac{\boldsymbol{{sin}}\mathrm{3}\boldsymbol{{x}}}{\mathrm{3}\boldsymbol{{x}}}} \\ $$$$\boldsymbol{{l}}=\frac{\mathrm{2}−\mathrm{8}−\mathrm{16}}{−\mathrm{492}}=\frac{\mathrm{22}}{\mathrm{492}}=\frac{\mathrm{11}}{\mathrm{246}} \\ $$$$\boldsymbol{{l}}=\frac{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\boldsymbol{{sinx}}−\mathrm{2}\boldsymbol{{tanx}}+\boldsymbol{{x}}^{\mathrm{3}} }{\boldsymbol{{x}}^{\mathrm{5}} }}{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{6}\boldsymbol{{x}}−\mathrm{2}\boldsymbol{{sin}}\mathrm{3}\boldsymbol{{x}}−\mathrm{9}\boldsymbol{{x}}^{\mathrm{3}} }{\boldsymbol{{x}}^{\mathrm{5}} }} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\boldsymbol{{sinx}}−\mathrm{2}\boldsymbol{{tanx}}+\boldsymbol{{x}}^{\mathrm{3}} }{\mathrm{6}\boldsymbol{{x}}−\mathrm{2}\boldsymbol{{sin}}\mathrm{3}\boldsymbol{{x}}−\mathrm{9}\boldsymbol{{x}}^{\mathrm{3}} }=\frac{\mathrm{0}}{\mathrm{0}}\boldsymbol{{fi}} \\ $$$$\boldsymbol{{to}}\:\boldsymbol{{apply}}\:\boldsymbol{{hospital}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\boldsymbol{{cosx}}−\mathrm{2}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)+\mathrm{3}\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{6}−\mathrm{6}\boldsymbol{{cos}}\mathrm{3}\boldsymbol{{x}}−\mathrm{27}\overset{\mathrm{2}} {\boldsymbol{{x}}}}=\frac{\mathrm{0}}{\mathrm{0}}\boldsymbol{{fi}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2}\boldsymbol{{sinx}}−\mathrm{4}\boldsymbol{{tanx}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)+\mathrm{6}\boldsymbol{{x}}}{+\mathrm{18}\boldsymbol{{sin}}\mathrm{3}\boldsymbol{{x}}−\mathrm{54}\boldsymbol{{x}}}=\frac{\mathrm{0}}{\mathrm{0}}\:\boldsymbol{{fi}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2}\boldsymbol{{cosx}}−\mathrm{4}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)^{\mathrm{2}} −\mathrm{8}\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)+\mathrm{6}}{\mathrm{54}\boldsymbol{{cos}}\mathrm{3}\boldsymbol{{x}}−\mathrm{54}}=\frac{\mathrm{0}}{\mathrm{0}}=\boldsymbol{{fi}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\boldsymbol{{sinx}}−\mathrm{8}\boldsymbol{{tanx}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)^{\mathrm{2}} −\mathrm{16}\boldsymbol{{tan}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)^{\mathrm{2}} −\mathrm{16}\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)}{−\mathrm{164}\boldsymbol{{sin}}\mathrm{3}\boldsymbol{{x}}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\frac{\boldsymbol{{sinx}}}{\boldsymbol{{x}}}−\mathrm{8}\frac{\boldsymbol{{tanx}}}{\boldsymbol{{x}}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)−\mathrm{16}\frac{\boldsymbol{{tanx}}}{\boldsymbol{{x}}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)^{\mathrm{2}} −\mathrm{16}\frac{\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}}{\boldsymbol{{x}}}\left(\mathrm{1}+\boldsymbol{{ta}}\overset{\mathrm{2}} {\boldsymbol{{n}x}}\right)}{−\mathrm{492}\frac{\boldsymbol{{sin}}\mathrm{3}\boldsymbol{{x}}}{\mathrm{3}\boldsymbol{{x}}}} \\ $$$$\boldsymbol{{l}}=\frac{\mathrm{2}−\mathrm{8}−\mathrm{16}}{−\mathrm{492}}=\frac{\mathrm{22}}{\mathrm{492}}=\frac{\mathrm{11}}{\mathrm{246}} \\ $$$$ \\ $$$$\mathrm{l}> \\ $$$$ \\ $$$$\mathrm{l}> \\ $$
Commented by Ar Brandon last updated on 26/Dec/22
C'est mieux ainsi ������
Answered by Ar Brandon last updated on 26/Dec/22
L=lim_(x→0) ((2sinx−2tanx+x^3 )/(6x−2sin3x−9x^3 )) [sinx→x−(x^3 /(3!))+(x^5 /(5!)): tanx→x+(x^3 /3)+((2x^5 )/(15))] =lim_(x→0) ((2(x−(x^3 /6)+(x^5 /(120)))−2(x+(x^3 /3)+((2x^5 )/(15)))+x^3 )/(6x−2(3x−((27x^3 )/6)+((243x^5 )/(120)))−9x^3 )) =lim_(x→0) ((−(1/4)x^5 )/(−((243)/(60))x^5 ))=(5/(81))
$$\mathscr{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2sin}{x}−\mathrm{2tan}{x}+{x}^{\mathrm{3}} }{\mathrm{6}{x}−\mathrm{2sin3}{x}−\mathrm{9}{x}^{\mathrm{3}} }\: \\ $$$$\:\:\left[\mathrm{sin}{x}\rightarrow{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}:\:\mathrm{tan}{x}\rightarrow{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2}{x}^{\mathrm{5}} }{\mathrm{15}}\right] \\ $$$$\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}+\frac{{x}^{\mathrm{5}} }{\mathrm{120}}\right)−\mathrm{2}\left({x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2}{x}^{\mathrm{5}} }{\mathrm{15}}\right)+{x}^{\mathrm{3}} }{\mathrm{6}{x}−\mathrm{2}\left(\mathrm{3}{x}−\frac{\mathrm{27}{x}^{\mathrm{3}} }{\mathrm{6}}+\frac{\mathrm{243}{x}^{\mathrm{5}} }{\mathrm{120}}\right)−\mathrm{9}{x}^{\mathrm{3}} } \\ $$$$\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{5}} }{−\frac{\mathrm{243}}{\mathrm{60}}{x}^{\mathrm{5}} }=\frac{\mathrm{5}}{\mathrm{81}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *