Menu Close

L-lim-x-pi-3-8cos-2-5x-2cosx-3-4cos-2-5x-8cosx-5-

Tinku Tara 0 Comments
Pin




Question Number 144473 by SOMEDAVONG last updated on 25/Jun/21
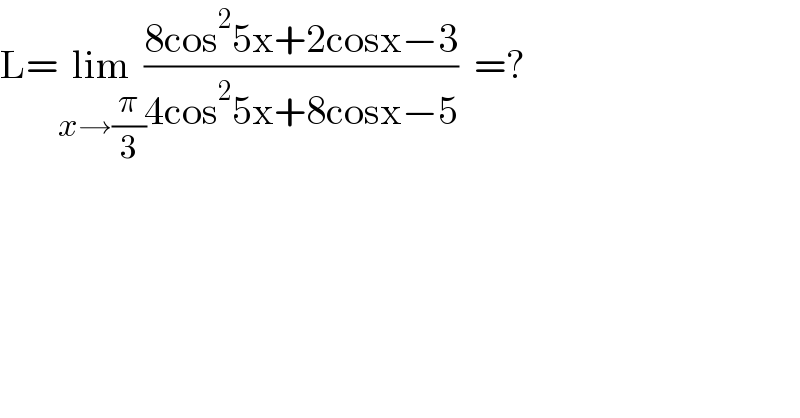
L=lim_(x→(π/3)) ((8cos^2 5x+2cosx−3)/(4cos^2 5x+8cosx−5)) =?
$$\mathrm{L}=\underset{{x}\rightarrow\frac{\pi}{\mathrm{3}}} {\mathrm{lim}}\frac{\mathrm{8cos}^{\mathrm{2}} \mathrm{5x}+\mathrm{2cosx}−\mathrm{3}}{\mathrm{4cos}^{\mathrm{2}} \mathrm{5x}+\mathrm{8cosx}−\mathrm{5}}\:\:=? \\ $$
Answered by mathmax by abdo last updated on 25/Jun/21
L=lim_(x→(π/3)) ((8(((1+cos(10x))/2))+2cosx−3)/(4(((1+cos(10x))/2))+8cosx −5)) =lim_(x→(π/3)) ((4+4cos(10x)+2cosx−3)/(2+2cos(10x)+8cosx −5)) =lim_(x→(π/3)) ((4cos(10x)+2cosx+1)/(2cos(10x)+8cosx−3)) =lim_(x→(π/3)) ((−40sin(10x)−2sinx)/(−20sin(10x)−8sinx)) (hospital) =((40sin(((10π)/3))+2sin((π/3)))/(20sin(10(π/3))+8sin((π/3))))=((20sin(π+(π/3))+((√3)/2))/(10sin(π+(π/3))+4.((√3)/2))) =((−20.((√3)/2)+((√3)/2))/(−10.((√3)/2)+2(√3)))=((−10(√3)+((√3)/2))/(−5(√3)+2(√3)))=((−19(√3))/(2(−3(√3)))) =((19)/6)
$$\mathrm{L}=\mathrm{lim}_{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{3}}} \:\:\:\:\:\:\:\frac{\mathrm{8}\left(\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)}{\mathrm{2}}\right)+\mathrm{2cosx}−\mathrm{3}}{\mathrm{4}\left(\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{10x}\right)}{\mathrm{2}}\right)+\mathrm{8cosx}\:−\mathrm{5}} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{3}}} \:\:\:\frac{\mathrm{4}+\mathrm{4cos}\left(\mathrm{10x}\right)+\mathrm{2cosx}−\mathrm{3}}{\mathrm{2}+\mathrm{2cos}\left(\mathrm{10x}\right)+\mathrm{8cosx}\:−\mathrm{5}} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{3}}} \:\:\:\:\frac{\mathrm{4cos}\left(\mathrm{10x}\right)+\mathrm{2cosx}+\mathrm{1}}{\mathrm{2cos}\left(\mathrm{10x}\right)+\mathrm{8cosx}−\mathrm{3}} \\ $$$$=\mathrm{lim}_{\mathrm{x}\rightarrow\frac{\pi}{\mathrm{3}}} \:\:\:\frac{−\mathrm{40sin}\left(\mathrm{10x}\right)−\mathrm{2sinx}}{−\mathrm{20sin}\left(\mathrm{10x}\right)−\mathrm{8sinx}}\:\:\left(\mathrm{hospital}\right) \\ $$$$=\frac{\mathrm{40sin}\left(\frac{\mathrm{10}\pi}{\mathrm{3}}\right)+\mathrm{2sin}\left(\frac{\pi}{\mathrm{3}}\right)}{\mathrm{20sin}\left(\mathrm{10}\frac{\pi}{\mathrm{3}}\right)+\mathrm{8sin}\left(\frac{\pi}{\mathrm{3}}\right)}=\frac{\mathrm{20sin}\left(\pi+\frac{\pi}{\mathrm{3}}\right)+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\mathrm{10sin}\left(\pi+\frac{\pi}{\mathrm{3}}\right)+\mathrm{4}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \\ $$$$=\frac{−\mathrm{20}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{−\mathrm{10}.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}}}=\frac{−\mathrm{10}\sqrt{\mathrm{3}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{−\mathrm{5}\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{3}}}=\frac{−\mathrm{19}\sqrt{\mathrm{3}}}{\mathrm{2}\left(−\mathrm{3}\sqrt{\mathrm{3}}\right)}\:=\frac{\mathrm{19}}{\mathrm{6}} \\ $$
Answered by EDWIN88 last updated on 26/Jun/21
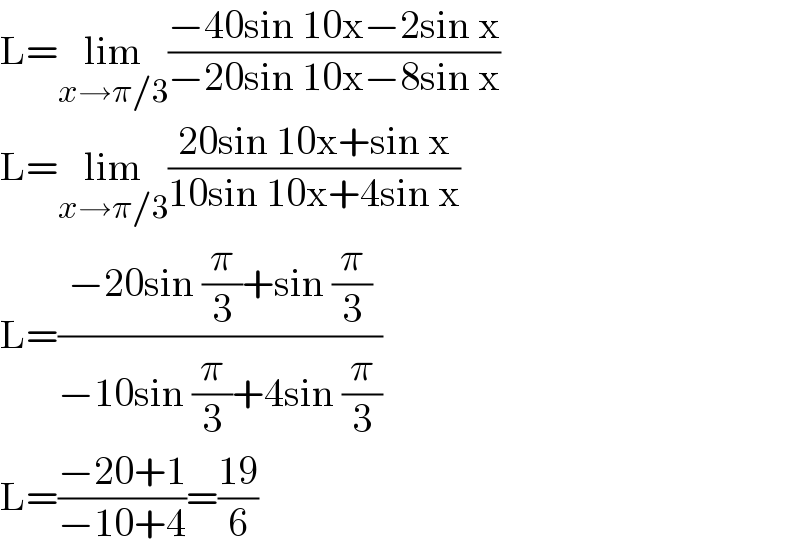
L=lim_(x→π/3) ((−40sin 10x−2sin x)/(−20sin 10x−8sin x)) L=lim_(x→π/3) ((20sin 10x+sin x)/(10sin 10x+4sin x)) L=((−20sin (π/3)+sin (π/3))/(−10sin (π/3)+4sin (π/3))) L=((−20+1)/(−10+4))=((19)/6)
$$\mathrm{L}=\underset{{x}\rightarrow\pi/\mathrm{3}} {\mathrm{lim}}\frac{−\mathrm{40sin}\:\mathrm{10x}−\mathrm{2sin}\:\mathrm{x}}{−\mathrm{20sin}\:\mathrm{10x}−\mathrm{8sin}\:\mathrm{x}} \\ $$$$\mathrm{L}=\underset{{x}\rightarrow\pi/\mathrm{3}} {\mathrm{lim}}\frac{\mathrm{20sin}\:\mathrm{10x}+\mathrm{sin}\:\mathrm{x}}{\mathrm{10sin}\:\mathrm{10x}+\mathrm{4sin}\:\mathrm{x}} \\ $$$$\mathrm{L}=\frac{−\mathrm{20sin}\:\frac{\pi}{\mathrm{3}}+\mathrm{sin}\:\frac{\pi}{\mathrm{3}}}{−\mathrm{10sin}\:\frac{\pi}{\mathrm{3}}+\mathrm{4sin}\:\frac{\pi}{\mathrm{3}}} \\ $$$$\mathrm{L}=\frac{−\mathrm{20}+\mathrm{1}}{−\mathrm{10}+\mathrm{4}}=\frac{\mathrm{19}}{\mathrm{6}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *