Question Number 28993 by abdo imad last updated on 02/Feb/18

$${L}\:{means}\:{laplacr}\:{trsnsform}\:{find}\:{L}\:\left({sin}\left({at}\right)\right) \\ $$$${and}\:{L}\left({cos}\left({at}\right)\right). \\ $$
Answered by sma3l2996 last updated on 03/Feb/18
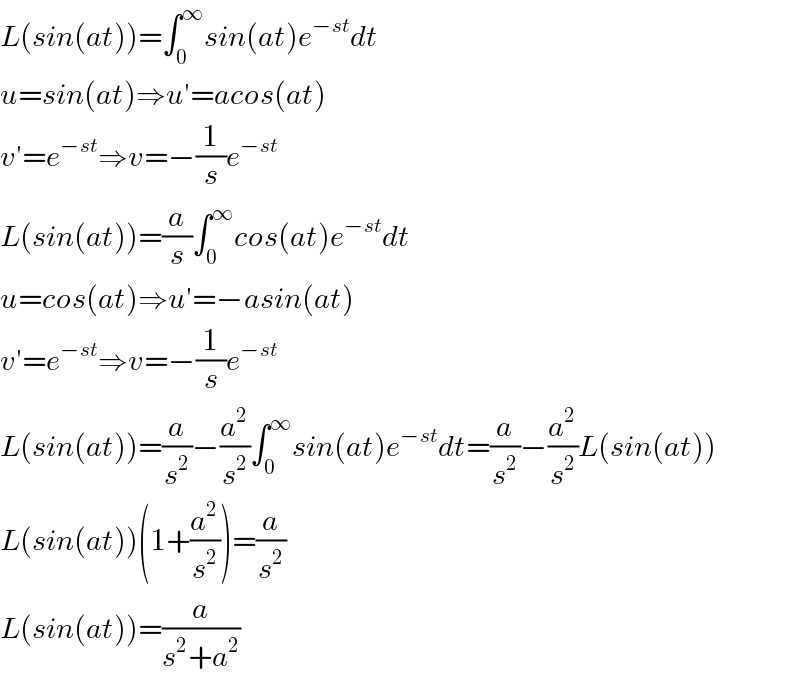
$${L}\left({sin}\left({at}\right)\right)=\int_{\mathrm{0}} ^{\infty} {sin}\left({at}\right){e}^{−{st}} {dt} \\ $$$${u}={sin}\left({at}\right)\Rightarrow{u}'={acos}\left({at}\right) \\ $$$${v}'={e}^{−{st}} \Rightarrow{v}=−\frac{\mathrm{1}}{{s}}{e}^{−{st}} \\ $$$${L}\left({sin}\left({at}\right)\right)=\frac{{a}}{{s}}\int_{\mathrm{0}} ^{\infty} {cos}\left({at}\right){e}^{−{st}} {dt} \\ $$$${u}={cos}\left({at}\right)\Rightarrow{u}'=−{asin}\left({at}\right) \\ $$$${v}'={e}^{−{st}} \Rightarrow{v}=−\frac{\mathrm{1}}{{s}}{e}^{−{st}} \\ $$$${L}\left({sin}\left({at}\right)\right)=\frac{{a}}{{s}^{\mathrm{2}} }−\frac{{a}^{\mathrm{2}} }{{s}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} {sin}\left({at}\right){e}^{−{st}} {dt}=\frac{{a}}{{s}^{\mathrm{2}} }−\frac{{a}^{\mathrm{2}} }{{s}^{\mathrm{2}} }{L}\left({sin}\left({at}\right)\right) \\ $$$${L}\left({sin}\left({at}\right)\right)\left(\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{s}^{\mathrm{2}} }\right)=\frac{{a}}{{s}^{\mathrm{2}} } \\ $$$${L}\left({sin}\left({at}\right)\right)=\frac{{a}}{{s}^{\mathrm{2}} +{a}^{\mathrm{2}} } \\ $$
