l-n-i-m-n-nm-n-1-n-

Question Number 34092 by rahul 19 last updated on 30/Apr/18

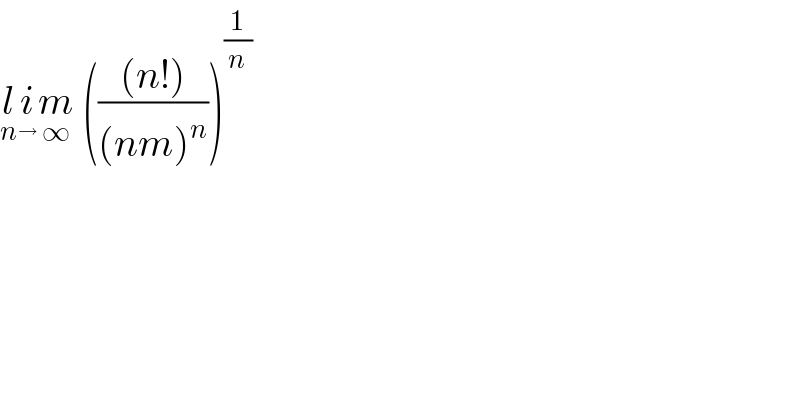
$$\underset{{n}} {{l}}\underset{} {{i}}\underset{\infty} {{m}}\:\left(\frac{\left({n}!\right)}{\left({nm}\right)^{{n}} }\right)^{\frac{\mathrm{1}}{{n}}} \\ $$

Commented by MJS last updated on 30/Apr/18

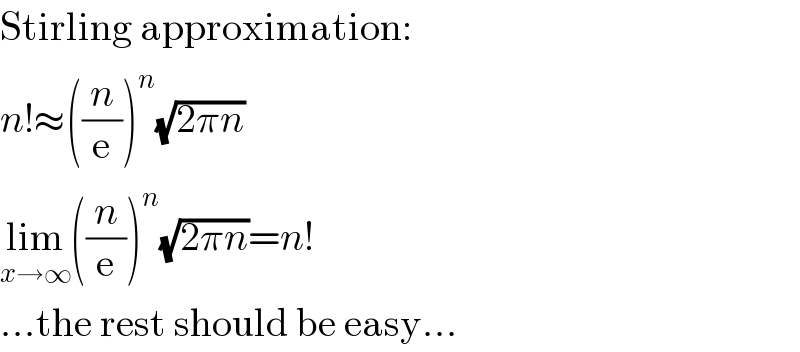
Stirling approximation: n!≈((n/e))^n (√(2πn)) lim_(x→∞) ((n/e))^n (√(2πn))=n! ...the rest should be easy...

$$\mathrm{Stirling}\:\mathrm{approximation}: \\ $$$${n}!\approx\left(\frac{{n}}{\mathrm{e}}\right)^{{n}} \sqrt{\mathrm{2}\pi{n}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{n}}{\mathrm{e}}\right)^{{n}} \sqrt{\mathrm{2}\pi{n}}={n}! \\ $$$$…\mathrm{the}\:\mathrm{rest}\:\mathrm{should}\:\mathrm{be}\:\mathrm{easy}… \\ $$

Commented by rahul 19 last updated on 30/Apr/18

$${pls}\:{do}\:\:{this}\:{by}\:'{stirling}\:{approximation}' \\ $$$${and}\:{also}\:{do}\:{explain}\:{what}'{s}\:{that}\:. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 01/May/18

$${there}\:{is}\:{a}\:{method}\:{to}\:{solve}\:{this}\:{type}\:{of}\:{problem} \\ $$$${let}\:{me}\:{share}\:{theorem}\:{first}\:{along}\:{with}\:{some} \\ $$$${problem}\:{then}\:{i}\:{shall}\:{solve}\:{it} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 01/May/18

Commented by tanmay.chaudhury50@gmail.com last updated on 01/May/18

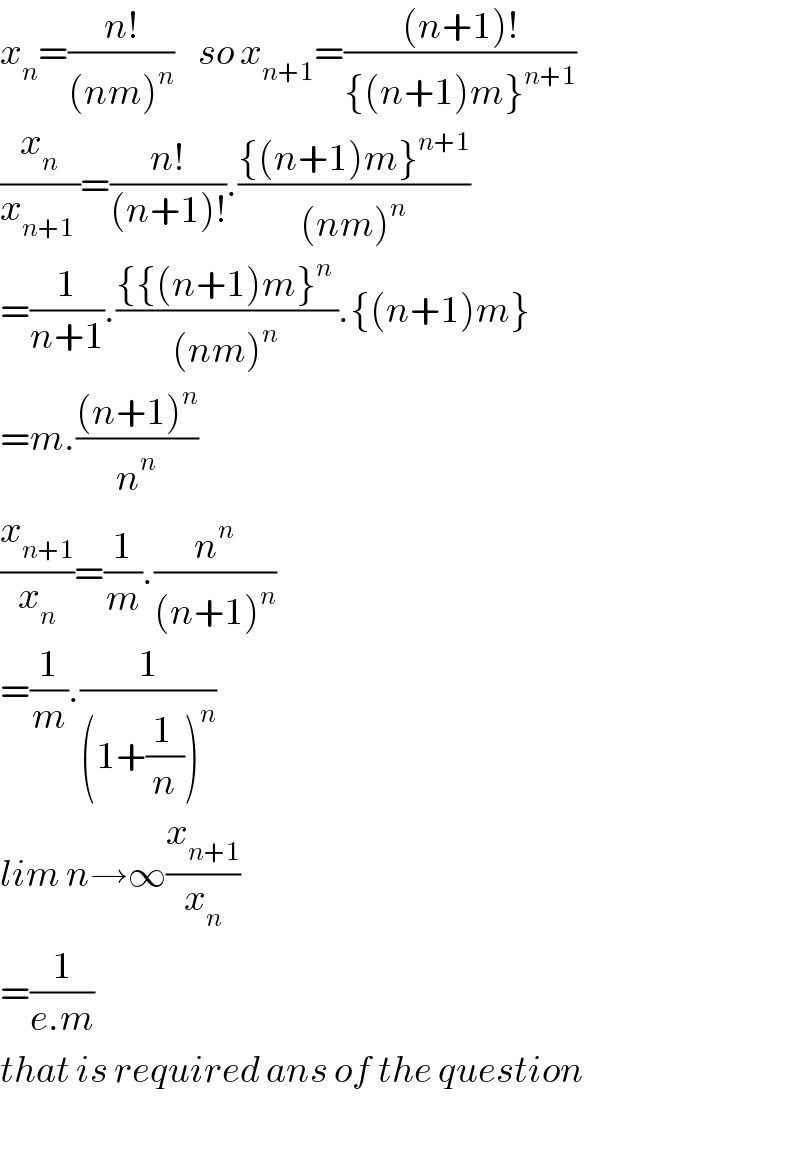
x_n =((n!)/((nm)^n )) so x_(n+1) =(((n+1)!)/({(n+1)m}^(n+1) )) (x_n /(x_(n+1) ))=((n!)/((n+1)!)).(({(n+1)m}^(n+1) )/((nm)^n )) =(1/(n+1)).(({{(n+1)m}^n )/((nm)^(n ) )).{(n+1)m} =m.(((n+1)^n )/n^n ) (x_(n+1) /x_n )=(1/m).(n^n /((n+1)^n )) =(1/m).(1/((1+((1 )/n))^n )) lim n→∞(x_(n+1) /x_n ) =(1/(e.m)) that is required ans of the question

$${x}_{{n}} =\frac{{n}!}{\left({nm}\right)^{{n}} }\:\:\:\:{so}\:{x}_{{n}+\mathrm{1}} =\frac{\left({n}+\mathrm{1}\right)!}{\left\{\left({n}+\mathrm{1}\right){m}\right\}^{{n}+\mathrm{1}} } \\ $$$$\frac{{x}_{{n}} }{{x}_{{n}+\mathrm{1}} \:}=\frac{{n}!}{\left({n}+\mathrm{1}\right)!}.\frac{\left\{\left({n}+\mathrm{1}\right){m}\right\}^{{n}+\mathrm{1}} }{\left({nm}\right)^{{n}} } \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}.\frac{\left\{\left\{\left({n}+\mathrm{1}\right){m}\right\}^{{n}} \:\right.}{\left({nm}\right)^{{n}\:} }.\left\{\left({n}+\mathrm{1}\right){m}\right\} \\ $$$$={m}.\frac{\left({n}+\mathrm{1}\right)^{{n}} }{{n}^{{n}} } \\ $$$$\frac{{x}_{{n}+\mathrm{1}} }{{x}_{{n}} }=\frac{\mathrm{1}}{{m}}.\frac{{n}^{{n}} }{\left({n}+\mathrm{1}\right)^{{n}} } \\ $$$$=\frac{\mathrm{1}}{{m}}.\frac{\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{1}\:}{{n}}\right)^{{n}} } \\ $$$${lim}\:{n}\rightarrow\infty\frac{{x}_{{n}+\mathrm{1}} }{{x}_{{n}} } \\ $$$$=\frac{\mathrm{1}}{{e}.{m}} \\ $$$${that}\:{is}\:{required}\:{ans}\:{of}\:{the}\:{question} \\ $$$$ \\ $$

Commented by rahul 19 last updated on 01/May/18

Thank you sir. well, i think stirling aprroximation is better (as it is short) . Anyways, it′s also a nice method.

$$\mathscr{T}{hank}\:{you}\:{sir}. \\ $$$${well},\:{i}\:{think}\:{stirling}\:{aprroximation} \\ $$$${is}\:{better}\:\left({as}\:{it}\:{is}\:{short}\right)\:.\:{Anyways}, \\ $$$${it}'{s}\:{also}\:{a}\:{nice}\:{method}. \\ $$

Commented by rahul 19 last updated on 01/May/18

pls do post the solutions of the given 5 Ques. also by this theorem.

Commented by math khazana by abdo last updated on 02/May/18

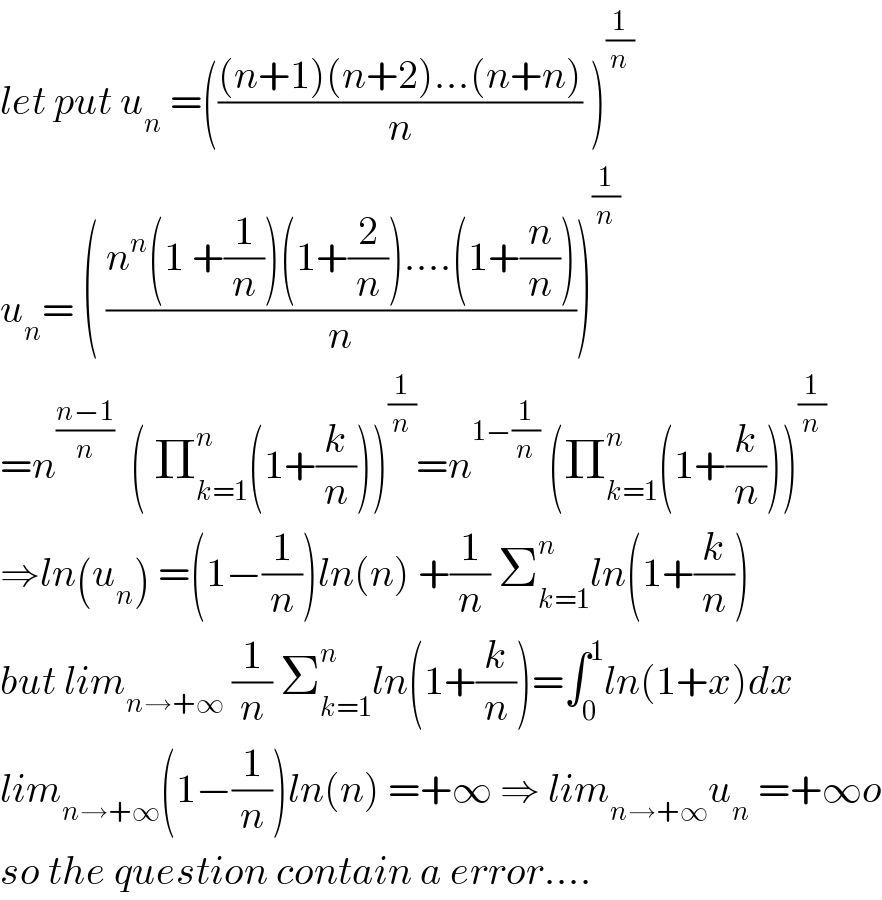
let put u_n =((((n+1)(n+2)...(n+n))/n) )^(1/n) u_n = ( ((n^n (1 +(1/n))(1+(2/n))....(1+(n/n)))/n))^(1/n) =n^((n−1)/n) ( Π_(k=1) ^n (1+(k/n)))^(1/n) =n^(1−(1/n)) (Π_(k=1) ^n (1+(k/n)))^(1/n) ⇒ln(u_n ) =(1−(1/n))ln(n) +(1/n) Σ_(k=1) ^n ln(1+(k/n)) but lim_(n→+∞) (1/n) Σ_(k=1) ^n ln(1+(k/n))=∫_0 ^1 ln(1+x)dx lim_(n→+∞) (1−(1/n))ln(n) =+∞ ⇒ lim_(n→+∞) u_n =+∞o so the question contain a error....

$${let}\:{put}\:{u}_{{n}} \:=\left(\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)…\left({n}+{n}\right)}{{n}}\:\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$${u}_{{n}} =\:\left(\:\frac{{n}^{{n}} \left(\mathrm{1}\:+\frac{\mathrm{1}}{{n}}\right)\left(\mathrm{1}+\frac{\mathrm{2}}{{n}}\right)….\left(\mathrm{1}+\frac{{n}}{{n}}\right)}{{n}}\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$$={n}^{\frac{{n}−\mathrm{1}}{{n}}} \:\:\left(\:\prod_{{k}=\mathrm{1}} ^{{n}} \left(\mathrm{1}+\frac{{k}}{{n}}\right)\right)^{\frac{\mathrm{1}}{{n}}} ={n}^{\mathrm{1}−\frac{\mathrm{1}}{{n}}} \:\left(\prod_{{k}=\mathrm{1}} ^{{n}} \left(\mathrm{1}+\frac{{k}}{{n}}\right)\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$$\Rightarrow{ln}\left({u}_{{n}} \right)\:=\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right){ln}\left({n}\right)\:+\frac{\mathrm{1}}{{n}}\:\sum_{{k}=\mathrm{1}} ^{{n}} {ln}\left(\mathrm{1}+\frac{{k}}{{n}}\right) \\ $$$${but}\:{lim}_{{n}\rightarrow+\infty} \:\frac{\mathrm{1}}{{n}}\:\sum_{{k}=\mathrm{1}} ^{{n}} {ln}\left(\mathrm{1}+\frac{{k}}{{n}}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}\right){dx} \\ $$$${lim}_{{n}\rightarrow+\infty} \left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right){ln}\left({n}\right)\:=+\infty\:\Rightarrow\:{lim}_{{n}\rightarrow+\infty} {u}_{{n}} \:=+\infty{o} \\ $$$${so}\:{the}\:{question}\:{contain}\:{a}\:{error}…. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 03/May/18

Answered by MJS last updated on 30/Apr/18

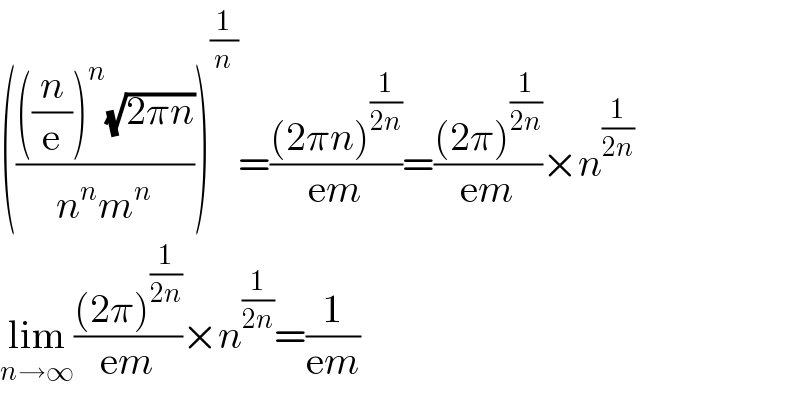
(((((n/e))^n (√(2πn)))/(n^n m^n )))^(1/n) =(((2πn)^(1/(2n)) )/(em))=(((2π)^(1/(2n)) )/(em))×n^(1/(2n)) lim_(n→∞) (((2π)^(1/(2n)) )/(em))×n^(1/(2n)) =(1/(em))

$$\left(\frac{\left(\frac{{n}}{\mathrm{e}}\right)^{{n}} \sqrt{\mathrm{2}\pi{n}}}{{n}^{{n}} {m}^{{n}} }\right)^{\frac{\mathrm{1}}{{n}}} =\frac{\left(\mathrm{2}\pi{n}\right)^{\frac{\mathrm{1}}{\mathrm{2}{n}}} }{\mathrm{e}{m}}=\frac{\left(\mathrm{2}\pi\right)^{\frac{\mathrm{1}}{\mathrm{2}{n}}} }{\mathrm{e}{m}}×{n}^{\frac{\mathrm{1}}{\mathrm{2}{n}}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{2}\pi\right)^{\frac{\mathrm{1}}{\mathrm{2}{n}}} }{\mathrm{e}{m}}×{n}^{\frac{\mathrm{1}}{\mathrm{2}{n}}} =\frac{\mathrm{1}}{\mathrm{e}{m}} \\ $$

Commented by rahul 19 last updated on 30/Apr/18

my doubt is : how l_n i_ m_∞ n^(1/(2n)) = 1 ?

$${my}\:{doubt}\:{is}\::\: \\ $$$${how}\:\underset{{n}} {\mathrm{l}}\underset{} {\mathrm{i}}\underset{\infty} {\mathrm{m}}\:{n}^{\frac{\mathrm{1}}{\mathrm{2}{n}}} \:=\:\mathrm{1}\:? \\ $$

Commented by MJS last updated on 30/Apr/18

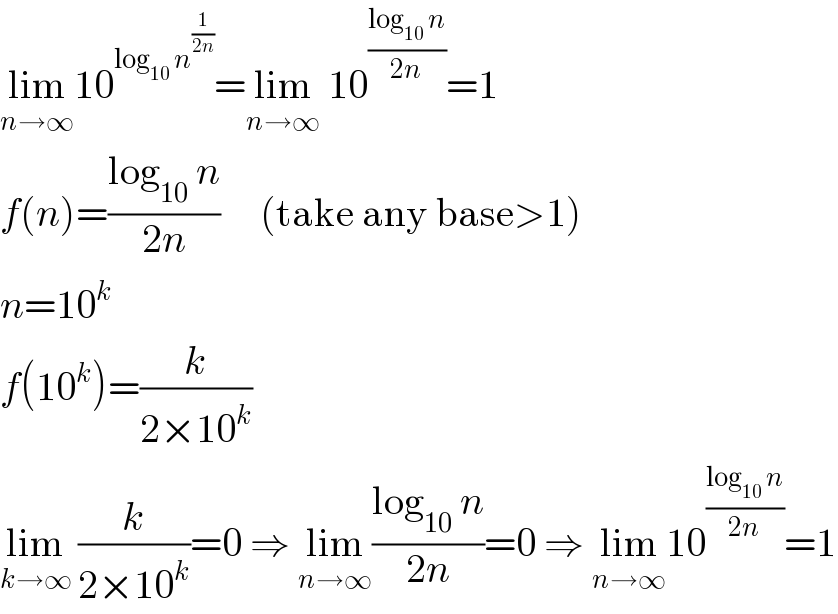
lim_(n→∞) 10^(log_(10) n^(1/(2n)) ) =lim_(n→∞) 10^((log_(10) n)/(2n)) =1 f(n)=((log_(10) n)/(2n)) (take any base>1) n=10^k f(10^k )=(k/(2×10^k )) lim_(k→∞) (k/(2×10^k ))=0 ⇒ lim_(n→∞) ((log_(10) n)/(2n))=0 ⇒ lim_(n→∞) 10^((log_(10) n)/(2n)) =1

$$\underset{{n}\rightarrow\infty} {\mathrm{lim}10}^{\mathrm{log}_{\mathrm{10}} \:{n}^{\frac{\mathrm{1}}{\mathrm{2}{n}}} } =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{10}^{\frac{\mathrm{log}_{\mathrm{10}} \:{n}}{\mathrm{2}{n}}} =\mathrm{1} \\ $$$${f}\left({n}\right)=\frac{\mathrm{log}_{\mathrm{10}} \:{n}}{\mathrm{2}{n}}\:\:\:\:\:\left(\mathrm{take}\:\mathrm{any}\:\mathrm{base}>\mathrm{1}\right) \\ $$$${n}=\mathrm{10}^{{k}} \\ $$$${f}\left(\mathrm{10}^{{k}} \right)=\frac{{k}}{\mathrm{2}×\mathrm{10}^{{k}} } \\ $$$$\underset{{k}\rightarrow\infty} {\mathrm{lim}}\:\frac{{k}}{\mathrm{2}×\mathrm{10}^{{k}} }=\mathrm{0}\:\Rightarrow\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{log}_{\mathrm{10}} \:{n}}{\mathrm{2}{n}}=\mathrm{0}\:\Rightarrow\:\underset{{n}\rightarrow\infty} {\mathrm{lim}10}^{\frac{\mathrm{log}_{\mathrm{10}} \:{n}}{\mathrm{2}{n}}} =\mathrm{1} \\ $$

Commented by rahul 19 last updated on 30/Apr/18

$$\mathscr{T}\mathrm{hank}\:\mathrm{you}\:\mathrm{sir}\:! \\ $$

Commented by prof Abdo imad last updated on 30/Apr/18

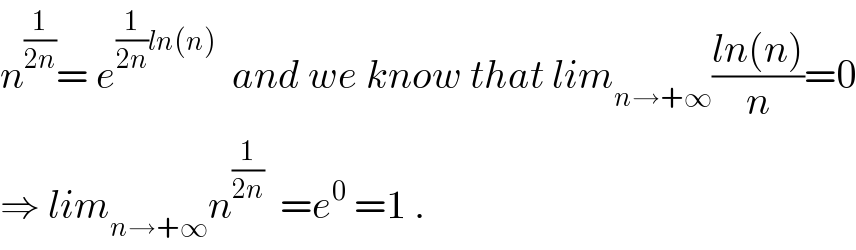
n^(1/(2n)) = e^((1/(2n))ln(n)) and we know that lim_(n→+∞) ((ln(n))/n)=0 ⇒ lim_(n→+∞) n^(1/(2n)) =e^0 =1 .

$${n}^{\frac{\mathrm{1}}{\mathrm{2}{n}}} =\:{e}^{\frac{\mathrm{1}}{\mathrm{2}{n}}{ln}\left({n}\right)} \:\:{and}\:{we}\:{know}\:{that}\:{lim}_{{n}\rightarrow+\infty} \frac{{ln}\left({n}\right)}{{n}}=\mathrm{0} \\ $$$$\Rightarrow\:{lim}_{{n}\rightarrow+\infty} {n}^{\frac{\mathrm{1}}{\mathrm{2}{n}}} \:\:={e}^{\mathrm{0}} \:=\mathrm{1}\:. \\ $$

Commented by rahul 19 last updated on 01/May/18