Question Number 100343 by student work last updated on 26/Jun/20
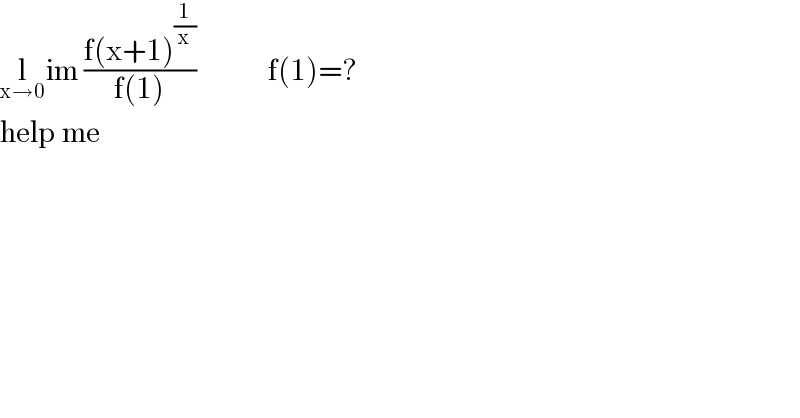
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{l}im}\:\frac{\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{x}}} }{\mathrm{f}\left(\mathrm{1}\right)}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{f}\left(\mathrm{1}\right)=? \\ $$$$\mathrm{help}\:\mathrm{me} \\ $$
Commented by student work last updated on 26/Jun/20

$$\mathrm{can}\:\mathrm{u}\:\mathrm{help}\:\mathrm{me}? \\ $$
Commented by student work last updated on 26/Jun/20
![lim_(x→0) [((f(x+1))/(f(1)))]^(1/x) =?](https://www.tinkutara.com/question/Q100453.png)
$$\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{m}}\left[\frac{\mathrm{f}\left(\mathrm{x}+\mathrm{1}\right)}{\mathrm{f}\left(\mathrm{1}\right)}\right]^{\frac{\mathrm{1}}{\mathrm{x}}} =? \\ $$
Commented by student work last updated on 26/Jun/20

$$\mathrm{f}\left(\mathrm{1}\right)=? \\ $$
Answered by mathmax by abdo last updated on 26/Jun/20

$$\mathrm{you}\:\mathrm{question}\:\mathrm{is}\:\mathrm{not}\:\mathrm{clear} \\ $$
