Question Number 94025 by Rasheed.Sindhi last updated on 16/May/20
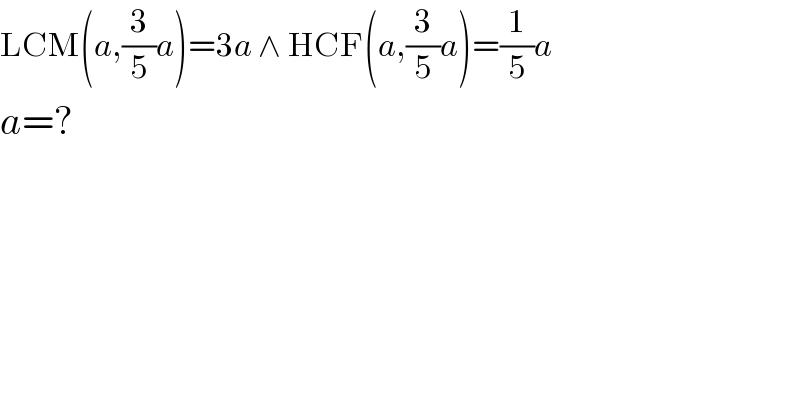
$$\mathrm{LCM}\left({a},\frac{\mathrm{3}}{\mathrm{5}}{a}\right)=\mathrm{3}{a}\:\wedge\:\mathrm{HCF}\left({a},\frac{\mathrm{3}}{\mathrm{5}}{a}\right)=\frac{\mathrm{1}}{\mathrm{5}}{a} \\ $$$${a}=? \\ $$
Commented by som(math1967) last updated on 16/May/20
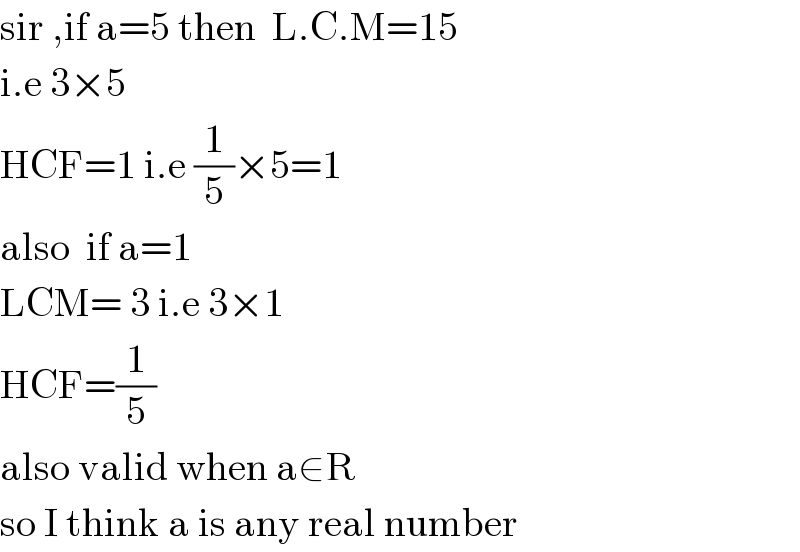
$$\mathrm{sir}\:,\mathrm{if}\:\mathrm{a}=\mathrm{5}\:\mathrm{then}\:\:\mathrm{L}.\mathrm{C}.\mathrm{M}=\mathrm{15} \\ $$$$\mathrm{i}.\mathrm{e}\:\mathrm{3}×\mathrm{5} \\ $$$$\mathrm{HCF}=\mathrm{1}\:\mathrm{i}.\mathrm{e}\:\frac{\mathrm{1}}{\mathrm{5}}×\mathrm{5}=\mathrm{1} \\ $$$$\mathrm{also}\:\:\mathrm{if}\:\mathrm{a}=\mathrm{1} \\ $$$$\mathrm{LCM}=\:\mathrm{3}\:\mathrm{i}.\mathrm{e}\:\mathrm{3}×\mathrm{1}\: \\ $$$$\mathrm{HCF}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\mathrm{also}\:\mathrm{valid}\:\mathrm{when}\:\mathrm{a}\in\mathrm{R} \\ $$$$\mathrm{so}\:\mathrm{I}\:\mathrm{think}\:\mathrm{a}\:\mathrm{is}\:\mathrm{any}\:\mathrm{real}\:\mathrm{number} \\ $$
Commented by Rasheed.Sindhi last updated on 16/May/20

$$\mathcal{T}{han}\mathcal{X}\:\:{Sir}! \\ $$
Commented by Rasheed.Sindhi last updated on 16/May/20

$${If}\:{a}\in\mathbb{Z}\:? \\ $$
Commented by som(math1967) last updated on 17/May/20
![If a=−3 [−3∈Z] ∴ LCM of −3,((−9)/5) is −9 i.e 3×−3 HCF is((−3)/5) i.e−3×(1/5) ∴true if a∈Z also we know Z∈R](https://www.tinkutara.com/question/Q94131.png)
$$\mathrm{If}\:\mathrm{a}=−\mathrm{3}\:\left[−\mathrm{3}\in\mathrm{Z}\right] \\ $$$$\therefore\:\mathrm{LCM}\:\mathrm{of}\:−\mathrm{3},\frac{−\mathrm{9}}{\mathrm{5}}\:\mathrm{is}\:−\mathrm{9}\: \\ $$$$\mathrm{i}.\mathrm{e}\:\mathrm{3}×−\mathrm{3}\:\mathrm{HCF}\:\mathrm{is}\frac{−\mathrm{3}}{\mathrm{5}}\:\mathrm{i}.\mathrm{e}−\mathrm{3}×\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\therefore\mathrm{true}\:\mathrm{if}\:\mathrm{a}\in\mathrm{Z} \\ $$$$\mathrm{also}\:\mathrm{we}\:\mathrm{know}\:\mathrm{Z}\in\mathrm{R} \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 17/May/20
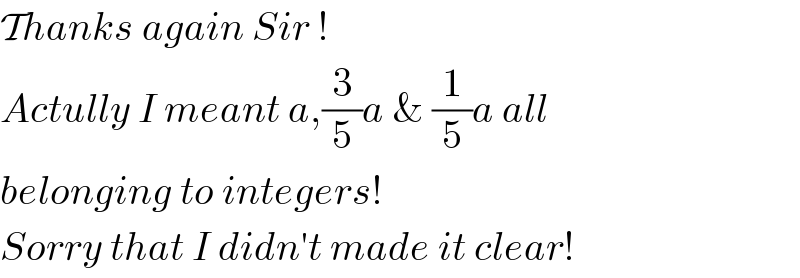
$$\mathcal{T}{hanks}\:{again}\:{Sir}\:! \\ $$$${Actully}\:{I}\:{meant}\:{a},\frac{\mathrm{3}}{\mathrm{5}}{a}\:\&\:\frac{\mathrm{1}}{\mathrm{5}}{a}\:{all} \\ $$$${belonging}\:{to}\:{integers}! \\ $$$${Sorry}\:{that}\:{I}\:{didn}'{t}\:{made}\:{it}\:{clear}! \\ $$
