Question Number 92889 by i jagooll last updated on 09/May/20

$$\mathrm{learning}\:\mathrm{distancing} \\ $$$$\int\:\mathrm{ln}\left(\sqrt{\mathrm{1}+\mathrm{x}}+\sqrt{\mathrm{1}−\mathrm{x}}\right)\:\mathrm{dx} \\ $$
Commented by john santu last updated on 09/May/20
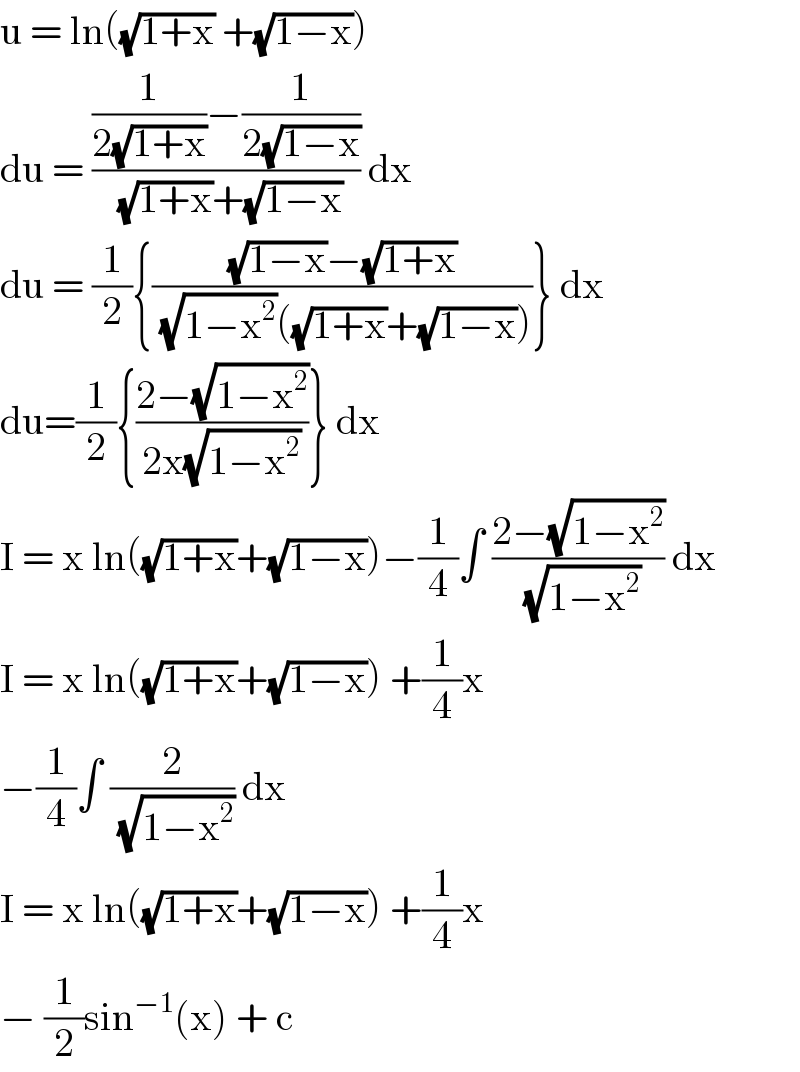
$$\mathrm{u}\:=\:\mathrm{ln}\left(\sqrt{\mathrm{1}+\mathrm{x}}\:+\sqrt{\mathrm{1}−\mathrm{x}}\right) \\ $$$$\mathrm{du}\:=\:\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+\mathrm{x}}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}−\mathrm{x}}}}{\:\sqrt{\mathrm{1}+\mathrm{x}}+\sqrt{\mathrm{1}−\mathrm{x}}}\:\mathrm{dx} \\ $$$$\mathrm{du}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\sqrt{\mathrm{1}−\mathrm{x}}−\sqrt{\mathrm{1}+\mathrm{x}}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\left(\sqrt{\mathrm{1}+\mathrm{x}}+\sqrt{\mathrm{1}−\mathrm{x}}\right)}\right\}\:\mathrm{dx} \\ $$$$\mathrm{du}=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{2}−\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}{\mathrm{2x}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\right\}\:\mathrm{dx} \\ $$$$\mathrm{I}\:=\:\mathrm{x}\:\mathrm{ln}\left(\sqrt{\mathrm{1}+\mathrm{x}}+\sqrt{\mathrm{1}−\mathrm{x}}\right)−\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\mathrm{2}−\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}\: \\ $$$$\mathrm{I}\:=\:\mathrm{x}\:\mathrm{ln}\left(\sqrt{\mathrm{1}+\mathrm{x}}+\sqrt{\mathrm{1}−\mathrm{x}}\right)\:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x} \\ $$$$−\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}\: \\ $$$$\mathrm{I}\:=\:\mathrm{x}\:\mathrm{ln}\left(\sqrt{\mathrm{1}+\mathrm{x}}+\sqrt{\mathrm{1}−\mathrm{x}}\right)\:+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}\: \\ $$$$−\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{x}\right)\:+\:\mathrm{c}\: \\ $$
